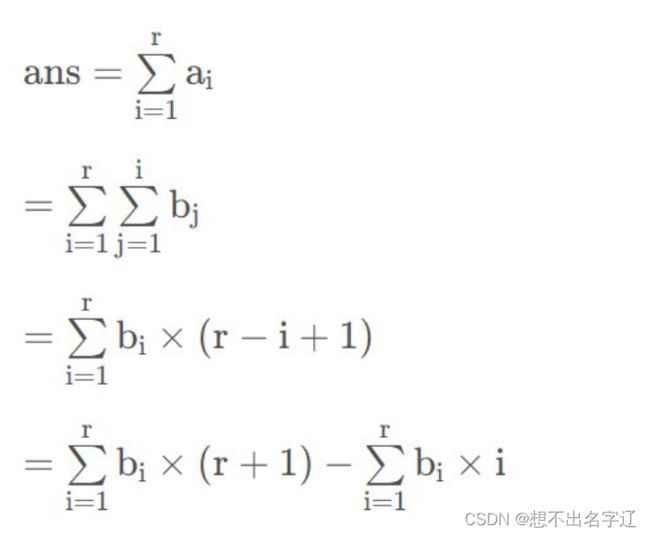树状数组及线段树入门(SDNU1665-1668)
目录
前言
树状数组
先导
单点修改区间查询
区间修改区间查询
线段树
先导
单点修改区间查询--递归形式
单点修改区间查询--非递归形式
区间修改区间查询--递归形式
区间修改区间查询--非递归形式
补充
前言
看了三天树,脑袋要烂掉了,我是从线段树开始学的然后再回头看的树状数组,找到了一些怪方法(师哥们没见过的useless方法),我尽量讲清楚一些,重点写自己理解得慢的地方。一下子看不懂很正常,感觉这个东西是需要时间理解,我第一天见他傻在那了,但是过了三天再看看觉得其实也挺好理解的(所以这几天我都学了什么效率好低啊啊)。
树状数组
先导
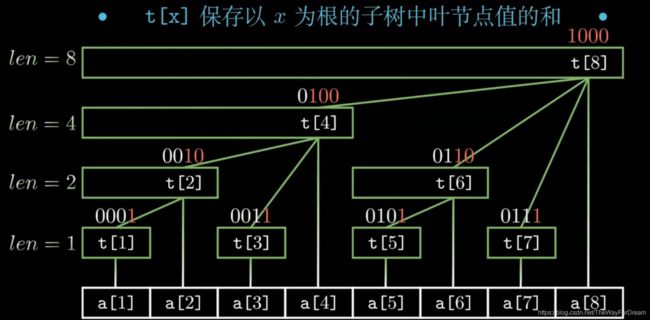
首先我们了解一下树状数组是个什么东西。
(这个图非常非常非常棒,后面不懂了就对着图看!)
a数组是我们的原数组,我们开个t数组(在下面的代码里sum数组为t)把a变成一个树的形式,这样在求和的时候就可以减少循环的次数,从而优化时间。这个树的构造原理就是按照二进制数字尾部0的个数分层,这样会更好算,至于怎么算,这里引入一个lowbit函数。很明显可以看出来这个算术方法是取反+1按位与。
ll lowbit(ll x) {
return x & (-x);
}对不起我讲不清楚,放个师哥的博客大家自己看吧浅谈lowbit运算_劭兮劭兮的博客-CSDN博客
我主要说一说lowbit函数求出来的是什么:根据定义我们知道这个求的是一个数的尾部第一个1及后面的0组成的十进制数,但这太抽象了;我们观察一下可以发现,这个东西求出来的是一个数与他右上节点(即父节点)之间的距离。我们看图还可以发现,如果这个数是奇数,那他的直接父节点就是比他大的最小偶数,如果是偶数,那父节点就是比他大的最小2^n。(这个发现没什么用)
单点修改区间查询
#include
using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
int n, q;
int arr[N];
ll sum[N];
ll lowbit(ll x) {
return x & (-x);
}
void build() {
for (int i = 1; i <= n; ++i) {
sum[i] += arr[i];
ll fa = i + lowbit(i);
if (fa <= n)
sum[fa] += sum[i];
}
}//O(n)建树 *1
void add(int p, int w) {
//arr[p] += w;//可改可不改
for (int i = p; i <= n; i += lowbit(i)) {
sum[i] += w;
}
}//单点修改 *2
ll ask(int x) {
ll ans = 0;
for (int i = x; i > 0; i -= lowbit(i)) {//注意别错
ans += sum[i];
}
return ans;
}//单点查询
void search(int l, int r) {
ll ans = ask(r) - ask(l - 1);
printf("%lld\n", ans);
return;
}//区间查询 *3
int main() {
//ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
scanf("%d %d", &n, &q);
memset(sum, 0, sizeof sum);
for (int i = 1; i <= n; ++i) {
scanf("%d", &arr[i]);
}
build();
while (q--) {
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
switch (a) {
case 1:
search(b, c);
break;
case 2:
add(b, c);
break;
}
}
return 0;
} *1:我的建树方法跟师哥们不一样,师哥们没建树,直接输入一个元素就把他加进树里,我没懂他们怎么干的,但是这样建树时间也是O(n),因为我们只遍历了一遍,从小往大捋,把每一个数都加到他直接父节点里,这样可以保证遍历到某个数时,他的子节点一定被加完了,不重不漏。(不懂就返回去看图手推)
*2:在先导里提到,lowbit函数求出来了他与父节点的距离,那加上他就直接让他变成了他爸爸,相当于我们找到叶节点,逐层递加直到某个节点没有爸爸。单点查询同理。
*3:l -> r == ( 1 -> r ) - ( 1 -> l )
区间修改区间查询
默认大家都会差分了我不细说了。
同样地,我们构造一个差分数组使每次修改在差分数组上操作,下面展示根据差分数组逆推ans:
看不懂没关系,这里有另一种形式:
ans=a[1]+a[2]+……+a[r-1]+a[r]
=tree[1]+(tree[1]+tree[2])+……+(tree[1]+……+tree[r])
=(tree[1]*(r))+(tree[2]*(r-1))+……(tree[r]*1)
=r*(tree[1]+tree[2]+……+tree[r]) - (tree[1]*0+tree[2]*1+……+tree[r]*(r-1))
=
= 上图的式子
那么我们就需要构造两个差分数组来维护区间和。
#include
using namespace std;
const int N = 1e6 + 5;
typedef long long ll;
ll n, q;
ll arr[N];//原数组
ll tree1[N], tree2[N];//差分数组1,2
//tree1=bi
//tree2=bi*(i-1)
ll lowbit(ll x) {
return x & (-x);
}
void add1(ll a, ll b) {
for (ll i = a; i <= n; i += lowbit(i)) {
tree1[i] += b;
}
}//加tree1
void add2(ll a, ll b) {
for (ll i = a; i <= n; i += lowbit(i)) {
tree2[i] += b;
}
}//加tree2
ll ask1(ll x) {
ll ans = 0;
for (ll i = x; i > 0; i -= lowbit(i)) {
ans += tree1[i];
}
return ans;
}
ll ask2(ll x) {
ll ans = 0;
for (ll i = x; i > 0; i -= lowbit(i)) {
ans += tree2[i];
}
return ans;
}
//单点查询
ll solve(ll x) {
return (x) * ask1(x) - ask2(x);
}//1 -> x区间查询
void search(ll l, ll r) {
ll ans = 0;
ans = solve(r) - solve(l - 1);
printf("%lld\n", ans);
}//区间查询
int main() {
//ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);//这个是解绑cin cout
scanf("%lld %lld", &n, &q);
for (ll i = 1; i <= n; ++i) {
scanf("%lld", &arr[i]);
add1(i, arr[i] - arr[i - 1]);
add2(i, (arr[i] - arr[i - 1]) * (i - 1));
//tree2[i]=tree1[i]*(i-1)
}
while (q--) {
ll a, b, c, d;
scanf("%lld", &a);
switch (a) {
case 1:
scanf("%lld %lld", &b, &c);
search(b, c);
break;
case 2:
scanf("%lld %lld %lld", &b, &c, &d);
add1(b, d);
add1(c + 1, -d);
add2(b, d * (b - 1));
add2(c + 1, -d * c);
break;
}
}
return 0;
} 树状数组就差不多到这里辣,其实还有二维数组但我肝不动了,过段时间再说吧。
线段树
先导
来看看线段树是个什么东西。
![]()
( 红色字为原数组下标;黑色字为线段树存储下标;红色区间为该下标存储的内容。)
我们注意到,线段树是一种二叉树,不同于树状数组,线段树越往叶节点延伸,下标就越大。我们对线段树下标的记法为:某个点的左儿子下标是其下标*2,右儿子下标是其下标*2+1,于是我们发现,左儿子必为偶数,右儿子必为奇数,反之亦然。这样就可满足图中的树形结构。那我们的数组该开多大呢?
严格来讲,实际上足够大的空间应为n向上扩充到大于等于n的最小2^k再*2;但是为了简便,我们可以直接记为4n。
单点修改区间查询--递归形式
#include
using namespace std;
#define int long long//一般#define int long long
const int N = 1e5 + 5;
typedef long long ll;//多用这个
int arr[N];
ll sum[4 * N];
void updat(int x) {
sum[x] = sum[x * 2] + sum[x * 2 + 1];
}//更新
void build(int p, int l, int r) {
if (l == r) {
sum[p] = arr[l];//说明到了叶节点
return;
} else {
int mid = (l + r) / 2;
build(p * 2, l, mid);//建左儿子
build(p * 2 + 1, mid + 1, r);//右儿子
}
updat(p);//每次建一个点就要更新他的父节点
}//建树
void change(int p, int w, int l, int r, int k) {
//arr[p]+=w;当前操作区间为(l,r);当前点为k
if (l == r) {
//找到了p
sum[k] += w;
return;
} else {
//二分,其实就是分别找他的左右儿子
int mid = (l + r) / 2;
if (p <= mid)
change(p, w, l, mid, k * 2);
else
change(p, w, mid + 1, r, k * 2 + 1);
updat(k);
//理解递归,在我们已完成递归操作后,说明已更新叶节点,此时应该逐层更新其父节点
}
}
int search(int L, int R, int l, int r, int k) {
//目标区间为(L,R);当前操作区间为(l,r);当前点为k
if (L <= l && R >= r)//当当前区间严格属于目标区间时,返回当前区间的值
return sum[k];
else {
int ans = 0;
int mid = (l + r) / 2;
//纯纯二分
if (L <= mid)
ans += search(L, R, l, mid, k * 2);
if (R > mid)
ans += search(L, R, mid + 1, r, k * 2 + 1);
return ans;
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
//解绑
int n, q;
cin >> n >> q;
for (int i = 1; i <= n; ++i) {
cin >> arr[i];
}
build(1, 1, n);
while (q--) {
int a, b, c;
cin >> a >> b >> c;
switch (a) {
case 1:
cout << search(b, c, 1, n, 1) << '\n';
break;
case 2:
change(b, c, 1, n, 1);
break;
}
}
return 0;
}
单点修改区间查询--非递归形式
(其实会递归就差不多够了,他俩时间复杂度是一样的)
参考博客线段树详解 (原理,实现与应用)_岩之痕的博客-CSDN博客_线段树
(揪了人家博客里的图, 但我们的实现方法略有不同,建议看看他写的,讲的很细很棒!)
求下标:回看先导中的图,我们观察到原数组下标和线段树存储下标的差值是一定的,这个差值是什么呢?其实就是我们计算出来的2^k-1,这里减不减1无所谓,下面会提到。这个意思也就是说,左下角为N(N=2^k)的二叉树,可以存N个元素,其中[1..N-1]是非叶节点,[N..2N-1]是叶节点。
找规律:假设我们要求[3,11],那么其实要求的是上图中紫圈的数,而蓝圈紧紧包围了紫圈,我们可以把区间转换为追踪两条蓝色链,上述博客讲的很清晰,不再赘述,我重点说我的优化。(双链汇集就是一个塔状的东西,下面会提到。)
优化:在他的博客里提到,如果我们要选取[1,5]区间就无法正确实现,所以要进行区间扩充,让线段树的下标从0起记,让n个元素转变为n+2个元素,其中头尾为0。
但如果我们追踪的不是蓝色链而是紫色链呢?令s=左端点,t=右端点,当s是左儿子时,其兄弟(他爸爸的右儿子)必在目标区间内,于是我们可以直接向上追踪他的父亲,t是右儿子时同理;当s是右儿子时,其兄弟必不在目标区间内,所以我们可以加上他,由于他是目标区间左边界,除去他之后,左边界就可以右移,直接让他成为他右边紧邻的兄弟,此时他必为左儿子,一定可以直接向上追踪,t是左儿子时同理。
追踪可以继续的条件是什么呢?即s<=t,在s==t时,我们找到了两链相交点,这时可保证塔尖区间加且仅加一次。(这里谢谢yxgg帮我de出了bug!!)
于是,我们再来看[1,5]区间,会发现这种方法可以计算!这样就不需要进行区间扩充了!求下标中是否-1的问题也可以想象为是否进行了区间扩充,其实扩不扩都可以的,影响不大。(笑死,师哥说这个很妙,他不知道我的初衷是看不懂原博客的位运算)
再想一遍:s是右儿子时加,t是左儿子时加。
#include
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
ll b = 1;//大于n的最小2^n
ll n, q;
ll arr[N];//原数组
ll sum[4 * N] = {0}; //线段树数组
void build(ll a) {
b = 1;
while (b < a + 2) {
b *= 2;
}
for (ll i = 1; i <= a; ++i) {
sum[i + b] = arr[i];
}
for (ll i = b - 1; i > 0; --i) {
sum[i] = sum[i * 2] + sum[i * 2 + 1];
}
return;
}
void Update(int p, int w) {
for (int now = p + b; now; now /= 2) {
sum[now] += w;
}
return;
}
void search(int l, int r) {
ll ans = 0;
for (int s = b + l, t = b + r; s <= t; s /= 2, t /= 2) {
if (s % 2 != 0)//s是右儿子时加
ans += sum[s++];
if (t % 2 == 0)//t是左儿子时加
ans += sum[t--];
}
printf("%lld\n", ans);
return;
}
int main() {
scanf("%d %d", &n, &q);
memset(arr, 0, sizeof arr);
arr[0] = 0;
for (int i = 1; i <= n; ++i) {
scanf("%d", &arr[i]);
}
build(n);
int a, l, r;
while (q--) {
scanf("%d %d %d", &a, &l, &r);
switch (a) {
case 1:
search(l, r);
break;
case 2:
Update(l, r);
break;
}
}
return 0;
} 区间修改区间查询--递归形式
不同于树状数组,我们对线段树区间修改的形式不再是建立差分数组,而是给他打上标记,注意在非叶节点时,我们存储的内容是一个区间而非一个元素,所以在标记到非叶节点时代表他所有的子孙都要继续加标记,此时标记的含义为本节点已更新,子节点标记待下推。
#include
using namespace std;
typedef long long ll;
const int N = 1e5 + 5;
ll sum[4 * N], add[4 * N]; //sum求和,add为懒惰标记
ll arr[N], n, q; //存原数组数据下标[1,n]
void updat(int x) {
sum[x] = sum[x * 2] + sum[x * 2 + 1];
}
void build(ll p, ll l, ll r) {
if (l == r) {
sum[p] = arr[l];
return;
} else {
int mid = (l + r) / 2;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
}
updat(p);
}
void PushDown(ll now, ll ln, ll rn) {//下推标记
//ln,rn为左子树,右子树的数字数量。
if (add[now]) {
//下推标记
add[now * 2] += add[now];
add[now * 2 + 1] += add[now];
//修改子节点的sum使之与对应的add相对应
sum[now * 2] += add[now] * ln;
sum[now * 2 + 1] += add[now] * rn;
//清除本节点标记
add[now] = 0;
}
}
void Update(ll L, ll R, ll C, ll l, ll r, ll now) { //区间修改
//目标区间为[L,R],当前操作区间[l,r],当前节点为now
if (L <= l && r <= R) { //当当前区间严格属于目标区间
sum[now] += C * (r - l + 1); //更新数字和,向上保持正确
add[now] += C; //增加add标记,表示本区间的sum正确,子区间的sum仍需要根据add的值来调整
return ;
}
int mid = (l + r) / 2;
PushDown(now, mid - l + 1, r - mid); //下推标记
if (L <= mid)//这里判断左右子树跟[L,R]有无交集,有交集才递归
Update(L, R, C, l, mid, now * 2);
if (R > mid)
Update(L, R, C, mid + 1, r, now * 2 + 1);
updat(now);//更新本节点信息
}
ll search(ll L, ll R, ll l, ll r, ll now) {
//目标区间为[L,R],当前操作区间[l,r],当前节点为now
if (L <= l && r <= R) {
//在区间内,直接返回
return sum[now];
}
ll mid = (l + r) / 2;
//下推标记,否则sum可能不正确
PushDown(now, mid - l + 1, r - mid);
//累计答案
ll ANS = 0;
if (L <= mid)
ANS += search(L, R, l, mid, now * 2);
if (R > mid)
ANS += search(L, R, mid + 1, r, now * 2 + 1);
return ANS;
}
int main() {
//ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
scanf("%lld %lld", &n, &q);
for (ll i = 1; i <= n; ++i) {
scanf("%lld", &arr[i]);
}
build(1, 1, n);
while (q--) {
ll a, b, c, d;
scanf("%lld", &a);
switch (a) {
case 1:
scanf("%lld %lld", &b, &c);
cout << search(b, c, 1, n, 1) << '\n';
break;
case 2:
scanf("%lld %lld %lld", &b, &c, &d);
Update(b, c, d, 1, n, 1);
break;
}
}
return 0;
} 区间修改区间查询--非递归形式
同样地,还是看刚刚的塔,我们无法像递归一样自上而下更新所有元素,于是我们只更新塔边元素,把更新工作放到查询里,由于查询也是自下而上的,所以如果查询的区间与修改区间重合,那么查询塔和修改塔也必有重合,这时塔边元素相交时就会更新答案以保证正确性。
上述博客代码在oj上还是wa的就先不放了,可能是我哪里没考虑到。
----->2022.11.25更新,我真被自己蠢无语了,de了一上午bug原来是因为没开ll,A了,注意这是扩充数组的形式,单点修改那点优化放在这里好像有点点问题……需要改改才能用。
#include
using namespace std;
typedef long long ll;
//不开ll见祖宗!!!!
const int N = 1e5 + 5;
ll sum[4 * N], add[4 * N]; //sum求和,add为懒惰标记
ll arr[N], n, q; //存原数组数据下标[1,n]
ll b;
void build(ll n) {
b = 1;
while (b < n + 2)
b <<= 1;
for (int i = 1; i <= n; ++i)
sum[b + i] = arr[i];
for (int i = b - 1; i > 0; --i) {
sum[i] = sum[i << 1] + sum[i << 1 | 1];
add[i] = 0;
}
}
void Update(ll L, ll R, ll C) {
ll s, t, Ln = 0, Rn = 0, x = 1;
//Ln: s一路走来已经包含了几个数
//Rn: t一路走来已经包含了几个数
//x: 本层每个节点包含几个数
for (s = b + L - 1, t = b + R + 1; s ^ t ^ 1; s >>= 1, t >>= 1, x <<= 1) {
sum[s] += C * Ln;
sum[t] += C * Rn;
//更新sum,令本节点的sum值加上他所有出现变化的子孙的变化和。
if (~s & 1)
add[s ^ 1] += C, sum[s ^ 1] += C * x, Ln += x;
if ( t & 1)
add[t ^ 1] += C, sum[t ^ 1] += C * x, Rn += x;
//处理add,标记本节点,意为本节点sum值正确,其父值待修改。
//注意到,修改sum时需要乘改变元素的个数,而修改add标记时不需
//因为add只代表本区间内所有元素改变C
//这里的x很巧妙,是2^k,我们观察二叉树的结构,每层的节点数也为2^k。
}
for (; s; s >>= 1, t >>= 1) {
sum[s] += C * Ln;
sum[t] += C * Rn;
}
//更新上层sum,从下向上推,当到塔尖时不会再出现新的需要增加的元素
//所以我们只需要推到树顶把路过的每一个节点(即改变量所属集合)的sum值更新即可
}
ll Query(ll L, ll R) {
ll s, t, Ln = 0, Rn = 0, x = 1;
ll ans = 0;
for (s = b + L - 1, t = b + R + 1; s ^ t ^ 1; s >>= 1, t >>= 1, x <<= 1) {
if (add[s])
ans += add[s] * Ln;
if (add[t])
ans += add[t] * Rn;
//根据标记更新答案,如果当前节点带标记,说明他是修改塔的边界
//他的儿子们在塔内(是被修改数)且不带标记
if (~s & 1)
ans += sum[s ^ 1], Ln += x;
if ( t & 1)
ans += sum[t ^ 1], Rn += x;
//常规求和
}
for (; s; s >>= 1, t >>= 1) {
ans += add[s] * Ln;
ans += add[t] * Rn;
}
//处理上层标记,追踪目标塔的边界是否存在其他被修改元素。
return ans;
}
int main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
scanf("%lld %lld", &n, &q);
for (ll i = 1; i <= n; ++i) {
scanf("%lld", &arr[i]);
}
build(n);
while (q--) {
ll a, b, c, d;
scanf("%lld", &a);
switch (a) {
case 1:
scanf("%lld %lld", &b, &c);
cout << Query(b, c) << '\n';
break;
case 2:
scanf("%lld %lld %lld", &b, &c, &d);
Update(b, c, d);
break;
}
}
return 0;
} 补充
1. 树状数组适合写单点修改的题,是线段树的缩略版,可以用树状数组写的题一定可以用线段树,但是反过来却不一定。
CVyjgg的话:(qwq超神yjgg好强!)
Q: 一般用树状数组还是线段树?
A: 看情况,树状数组特别适合单点修改,通过单点修改能延伸出很多有意思的操作,而线段树就适合大型区间修改,树状数组写出来的题,线段树都能写,反过来不行,一般需要维护区间的东西很多的时候用线段树,也只能用线段树,但是线段树很笨重,写起来复杂,debug更复杂。树状数组对于单点修改写起来很简单,一般两三分钟就能写一颗树状数组,树状数组和差分结合可以实现一些稍微复杂一点点的区间维护,但是如果写的不熟练的话很容易出错。所以一般先看能不能用树状数组,可以简单实现的话就树状数组,不行的话就线段树。
2. 一般需要用到这个的题都有很多输入输出,要注意优化(关io或scanf或快读)。
3. 树状数组大大提高了空间利用率,只用开一倍空间就足够了,但是线段树需要开4n数组,浪费空间以保证各种操作的可执行性。
4. 线段树每一次操作(查询或修改)的时间复杂度都是logn的。
5. yjgg在看我代码的时候提到,我们一般写这样
typedef long long ll;//常用
#define ll long long//不常用
#define int long long//一般这么用我去查了一下这两个的区别但没太看懂,大概是酱紫:
#define是C语言中定义的语法,可以在预处理时进行单纯的字符串替换,不作正确性检查,只有在编译已被展开的源程序时才会发现可能的错误并报错。他没有自己的作用域,只要是之前定义过的宏就都可以用。
typedef是关键字,在编译时处理会进行类型检查。它在自己的作用域内给一个已经存在的类型一个别名,但不能在一个函数定义里面使用typedef。有自己的作用域。
他俩对指针的操作也不太一样,但我指针学的很差,想了解的可以自己去查查。
❤再次感谢yxgg和yjgg的指点!!!❤