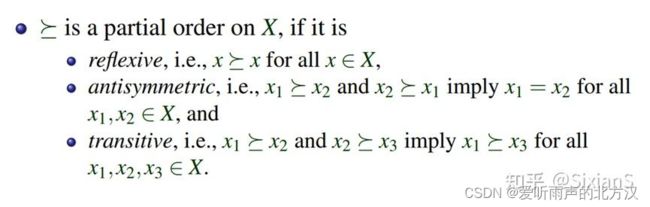经管博士科研基础【17】超模函数和低模函数

最近阅读Management Science上面的一篇文章，其中用到了超模函数，那么何为超模函数呢？听说还有一个低模函数（也有人称之为子模函数），又是什么呢？

咱们就得一一解决掉，否则后面就读不懂论文了。

1. 基本含义

而低模函数用来描述可替代产品，一个产品销量的增加引起另一个产品销量的减少。 

2. 理论背景

基本介绍：超模博弈和替代、互补性紧密相关，设定上依赖于lattice structure（lattice我们一般称之为格）。这套理论最早是运筹学家Topkins（1978，1979，1998）提出，经济学里是Bulow et al.（1985）引入策略互补和策略替代。诺奖得主Milgrom and Roberts（1990）、同期的Vives（1990）进一步集大成。Shapley在1995，1962，1971，1972的多篇文章中研究了与合作博弈相关的内容，就包含了超模博弈互补替代的思想。

3. 相关知识

首先要认识这个长得像大于等于的符号（partial order），这个符号可以暂时理解成大于等于号，有自反性、反对称性和传递性，但是任意取两个元素，可能没办法比（比如我对有的商品的preference我自己也不确定）。

什么叫lattice？对所有X中的x，y，存在：

• 上确界：z（在lattice里）比x、y都大，但是是比他们都大的里最小的。
• 下确界：z（在lattice里）比x、y都小，但是是比他们都小的里最大的。

二元欧氏空间上，任何两个点（x，y）是满足partial order的，但是不能让两个点进行比较（比如一个是x的大，一个是y的更大）。如果X是个圆（坐标系里），就不是lattice，因为z不在lattice里。如果X是个正方形，就是个lattice。 

Complete lattice（完全格）：任意多个元素都有上确界下确界。

 

超模博弈还分为 非合作超模博弈 和 合作超模博弈。这两种的在数学描述上都是基于lattices理论，所以有着紧密的联系。古诺竞争和伯川德竞争都可以用超模博弈来研究。

 

S^N是个笛卡尔乘积（低维最后形成高维），每个人的策略集乘起来，最后是个n维的（x1，x2，…，xn）。

 像v的这个数学符号，意思是每个维度都取最大；像倒v的这个，是每个维度取最小的意思。

解读：player i和j是pairwise strategic complements：对i来说，所有的si比ti严格大，对j来说，sj也比tj严格大，i、j以外的人取定一个策略。再满足（1）、（2）式。

（1）式左边：i选策略si和ti效用的差异（其他人选择都不变，包括j选择sj），这里可以理解成，si策略和ti策略差值对效用ui的边际贡献，因为前面说了si比ti严格大。左边的式子要大于右边当j选择tj的时候的i的效用变化。（2）式同理，主角从i变成了j。

直观的解读就是，j选sj而不是tj时，对i的边际效用促进更大。也可以理解为当j把自己的策略从小的tj变成大的sj时，对i来说提升自身的激励更大了（从ti到si）。这里的意义是：i、j两个人调整激励的方向是一致的，有了方向性和单调性，对求解均衡有帮助。

如果是策略替代博弈，就是把两个符号改成反过来的。

想要策略互补博弈存在，还需要满足以上两个假设：

假设1可以保证每个人的极大是可以取到的。假设2在比如格是linear的情况下，都是成立的

4. 超模函数

5. 超模函数的性质

右图是个L=R^2的二维空间，定义在图里的解读，就是红点的值和蓝点的值大于两个黄点的值之和。

理解：

1. 超模函数的交叉导大于等于0（判断易）（这可以帮助我们判别是否是超模函数）。此外，任何的一元函数都是超模的，式子永远成立的。即使是多元，判断交叉导也很容易。

2. 超模函数可以是离散的（用途广），定义域可以不连续，适用范围更广。

3.超模函数已经蕴含了任意两个人之间也是（前面说的）pairwise strategic complements（条件强）。

超模函数性质：

1. 纯策略纳什均衡存在。

2.不仅存在，还有个lattice结构（i.e.纯策略NE有个最大的均衡和最小的均衡）动态视角：如果起点合适，会收敛到最大/最小的均衡，有一些参数可以帮助做比较静态分析，可以解读经济学含义。

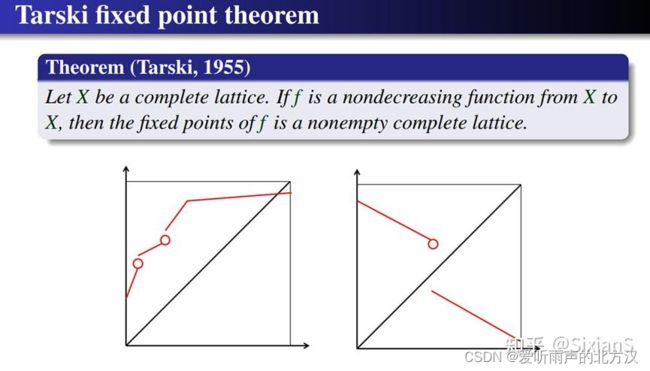
证明函数的存在性（Tarski不动点定理）

NE等价于一些最优反应的不动点。如果具备一些性质，我们就可以保证不动点存在（即NE存在）。这个定理说的是单调性的特点（如左图）：x是个complete lattice，f是个单调增的映射（保序变换），一定会有不动点存在（和45°线的交点），且不动点合在一起是一个complete lattice。

反过来不成立（如右图）：是个单调减的映射，不一定有不动点，可以直接“跳下来”，不和45°线相交。

6. 应用例子

6.1 Bertrand 竞争（价格竞争）

p_i是一个complete lattice；Q是需求量；是一个策略互补博弈（核心条件：通过交叉导=wij>0可知），一个厂商价格往下降，另一个也有激励往下降。其他零碎的条件也很容易验证。

古诺竞争也是同理，但是交叉导小于0，是策略替代博弈：比如一个厂商产出数量往上调，另一个厂商产出数量往下调（可以通过调整符号、扭曲lattice转为策略互补博弈）。

6.2 Diamond’s Search Model

a_i再complete lattice上；g（0）=0，g（1）=1；最优反应唯一且单调递增，说明是策略互补的。θ和ai有互补关系，可以解读成回报越高，大家努力水平越高。

转载于：如何简单地解释「超模（Supermodular）博弈」？ - 知乎