模拟喷泉码(入门四):Regularized Variable-Node LT Codes with Improved Erasure Floor Performance
2013《Regularized Variable-Node LT Codes with Improved Erasure Floor Performance》学习笔记
- 基于外部信息传递图(extrinsic information transfer charts,EXIT charts)优化CNs度分布,设计具有良好的CN度分布的二进制擦除信道(BEC)上的LT码
- 修改LT码编码过程以最大化最小VNs度,降低解码器误差下限
- 进一步应用于UEP LT并仿真研究传输性能
目录
- 1. 研究背景
- 2. 前置知识
-
- 2.1 LT码
- 2.2 节点度分布
- 2.3 分析解码器渐近性能的工具
- 3. 设计VNs度分布与性能分析
-
- 3.1 传统LT码的度分布
- 3.2 改进EEP-LT代码的擦除下限
- 3.3 改进正则化EEP-LT码
- 4. UEP-LT码的渐近分析
- 补充
1. 研究背景
因:时变信道使用固定速率码难以同时实现high throughput和high error resilience
↓
果:引入喷泉码,渐进式数据传输(收到的包不用等待发送端停止发送就能在接收端进行解码操作),LT码是第一个实际实现的无速率码
↓
因:LT码在二进制擦除信道(BEC)中性能优异,但噪声信道上错误下限较高,且编码和解码的复杂性随着块长度的增加而增加。论文Rateless codes on noisy channels分析了LT码在BEC信道和AWGN信道上的性能
↓
果1:Raptor码确保无速率码的高效编解码,可在噪声信道中降低错误下限
果2:LT码改进,主要方向有改进CNs的度分布、改进VNs的度分布(在编码过程中施加限制)
应用场景分类:
所有信息位同等重要→具备EEP(equal erasure protection)能力的编码方式
存在部分信息更重要→具备UEP(unequal erasure protection)能力的编码方式→无速率码
etc.
S. Arslan, P . Cosman, and L. Milstein, “Generalized unequal error protection LT codes for progressive data transmission,” IEEE Trans. Image Processing, vol. 21, no. 8, pp. 3586–3597, Aug. 2012
N. Rahnavard, B. V ellambi, and F. Fekri, “Rateless codes with unequal error protection property,” IEEE Trans. Inf. Theory, vol. 53, no. 4, pp. 1521–1532, 2007.
2. 前置知识
2.1 LT码
LT码是一种线性码,具有随机生成的稀疏生成矩阵。通过对随机选择的信息位的随机数进行异或运算,顺序生成编码位。
PS:矩阵结构同non-systematic low-density generator matrix (LDGM) code
所以根据J. Garcia-Frias and W. Zhong, “Approaching Shannon performance by iterative decoding of linear codes with low-density generator matrix,” IEEE Commun. Letters, vol. 7, no. 6, pp. 266–268, Jun. 2003和K. Liu and J. Garci, “Error floor analysis in LDGM codes,” in Proc. IEEE Int Symp. Inf. Theory, Austin, USA, Jun. 2010, pp. 734–738.可知限制误差下限的因素是VNs的最小度。
编码:对于K个VNs,在时刻 t t t,一共编码成 N t e N_{t}^{\mathrm{e}} Nte个CNs用于BEC信道传输
c t = G t u u = [ u 1 , u 2 , … , u K ] T c t = [ c 1 , c 2 , … , c N t e ] T \begin{array}{ll}\mathbf{c}_{t}=\mathbf{G}_{t} \mathbf{u} \\ \mathbf{u}=\left[u_{1}, u_{2}, \ldots, u_{K}\right]^{T} \\ \mathbf{c}_{t}=\left[c_{1}, c_{2}, \ldots, c_{N_{t}^{e}}\right]^{T} \end{array} ct=Gtuu=[u1,u2,…,uK]Tct=[c1,c2,…,cNte]T其中生成矩阵 G t \mathbf{G}_{t} Gt维度 N t e × K N_{t}^{\mathrm{e}} \times K Nte×K,其构造方法是逐行构造:从CN度分布中抽取一个度值 d c d_{c} dc,随机抽取该行中的 d c d_{c} dc置1.
编码过程会持续进行,解码器解码成功后反馈一个ACK给编码器,编码中止。
解码:
定义解码开销(overhead):
γ = N t d / K \gamma=N_{t}^{\mathrm{d}} / K γ=Ntd/K其中 N t d = N t e − N t ϵ = N t e − ϵ N t e = ( 1 − ϵ ) N t e N_{t}^{\mathrm{d}}=N_{t}^{\mathrm{e}}-N_{t}^{\epsilon}=N_{t}^{\mathrm{e}}-\epsilon N_{t}^{\mathrm{e}}=(1-\epsilon) N_{t}^{\mathrm{e}} Ntd=Nte−Ntϵ=Nte−ϵNte=(1−ϵ)Nte,表示解码器收到的bit数=发送-擦除。
2.2 节点度分布
CNs度分布和VNs度分布基本上定义了码字结构:
CNs度分布描述为概率集合, h = [ h 1 , h 2 , … , h m a x ] T \mathbf{h}=\left[h_{1}, h_{2}, \ldots, h_{max}\right]^{T} h=[h1,h2,…,hmax]T, 1 ≤ h max ≤ K 1 \leq h_{\max } \leq K 1≤hmax≤K,注意: ∑ h i = 1 \sum h_{i}=1 ∑hi=1,CNs的平均度 h a v g = ∑ j = 1 h max j h j h_{\mathrm{avg}}=\sum_{j=1}^{h_{\max }} j h_{j} havg=∑j=1hmaxjhj。
VNs度分布是一个可能存在的 v = [ v 1 , v 2 , … , v N t d ] T \mathbf{v}=\left[v_{1}, v_{2}, \ldots, v_{N_t^{d}}\right]^{T} v=[v1,v2,…,vNtd]T, ∑ i = 0 N t d v i = 1 \sum_{i=0}^{N_{t}^{\mathrm{d}}} v_{i}=1 ∑i=0Ntdvi=1,由于随机且均匀地抽取VNs构造CN,VNs的度分布式一个二项分布: v i = ( N t d i ) ( h a v g K ) i ( 1 − h a v g K ) N t d − i v_{i}=\left(\begin{array}{c} N_{t}^{\mathrm{d}} \\ i \end{array}\right)\left(\frac{h_{\mathrm{avg}}}{K}\right)^{i}\left(1-\frac{h_{\mathrm{avg}}}{K}\right)^{N_{t}^{\mathrm{d}}-i} vi=(Ntdi)(Khavg)i(1−Khavg)Ntd−i如果 K K K and N t d ↑ N_{t}^{\mathrm{d}}↑ Ntd↑,VNs的度分布会趋近于泊松分布:
v ( x ) = ∑ i = 0 N t d v i x i ≈ e v avg ( x − 1 ) v(x)=\sum_{i=0}^{N_{t}^{\mathrm{d}}} v_{i} x^{i}\approx e^{v_{\text {avg }}(x-1)} v(x)=i=0∑Ntdvixi≈evavg (x−1)其中泊松参数即 v avg = h a v g N t d K = ∑ i = 0 N t d i v i v_{\text {avg}}=h_{\mathrm{avg}} \frac{N_{t}^{\mathrm{d}}}{K}=\sum_{i=0}^{N_{t}^{\mathrm{d}}} i v_{i} vavg=havgKNtd=∑i=0Ntdivi
为分析解码器的渐进性能,引入edge-perspective degree distributions:
CNs的edge-degree分布定义为 ρ ( x ) = h ′ ( x ) / h ′ ( 1 ) \rho(x)=h^{\prime}(x) / h^{\prime}(1) ρ(x)=h′(x)/h′(1),其中 h ( x ) = ∑ j = 1 h max h j x j h(x)=\sum_{j=1}^{h_{\max }} h_{j} x^{j} h(x)=∑j=1hmaxhjxj, ρ j \rho_{j} ρj表示边来自于 i i i度CNs的概率。
VNs的edge-degree分布定义为 λ ( x ) = v ′ ( x ) / v ′ ( 1 ) \lambda(x)=v^{\prime}(x) / v^{\prime}(1) λ(x)=v′(x)/v′(1),其中 v ( x ) = ∑ i = 0 N t d v i x i v(x)=\sum_{i=0}^{N_{t}^{\mathrm{d}}} v_{i} x^{i} v(x)=∑i=0Ntdvixi, λ i \lambda_{i} λi表示边来自于 j j j度CNs的概率。
2.3 分析解码器渐近性能的工具
Density Evolution 跟踪VNs未成功恢复概率的平均值
通过解码过程的AND-OR树评估来确定,简略原理和过程可以参考入门三2.2节
EXIT Charts跟踪VNs和CNs之间在迭代过程中交换外部互信息,并供消息传递解码器使用。
在EXIT Charts分析中解码器操作呗建模为两个子解码器(CND和VND),通过对应的边缘交织器(edge interleavers)交换外部互信息。
TODO1:
A. Ashikhmin, G. Kramer, and S. ten Brink, “Extrinsic information transfer functions: Model and erasure channel properties,” IEEE Trans. Inf. Theory, vol. 50, no. 11, pp. 2657–2673, Nov. 2004.
术语介绍:
总结:Density Evolution和EXIT Charts分析都为BEC上的传输提供了准确的置信传播解码阈值。EXIT Charts分析在收敛阈值方面搜索良好的度分布通常可以表述为一个凸优化问题。
3. 设计VNs度分布与性能分析
3.1 传统LT码的度分布
度分布见sec 2.2
LT码的解码器开销 γ \gamma γ可以用edge-perspective degree distributions表示为 γ = ∑ j ρ j / j ∑ i λ i / i \gamma=\frac{\sum_{j} \rho_{j} / j}{\sum_{i} \lambda_{i} / i} γ=∑iλi/i∑jρj/j。VNs的edge-degree分布(反应CNs的度分布情况) λ i \lambda_{i} λi由于编码过程的随机抽选CNs的度是已知量,所以最小化 ∑ j ρ j / j \sum_{j} \rho_{j} / j ∑jρj/j(反应VNs的度分布情况)即课最小化解码器开销。该线性规划问题建模为:
min ∑ j ρ j / j such that ρ j ≥ 0 ∑ j ρ j = 1 λ i = i v i / v ′ ( 1 ) , i = 0 , 1 , … , N t d I E , C ( I A , C ) > I E , V − 1 ( I A , V ) . \begin{array}{ll} \min & \sum_{j} \rho_{j} / j \\ \text { such that } & \rho_{j} \geq 0 \\ & \sum_{j} \rho_{j}=1 \\ & \lambda_{i}=i v_{i} / v^{\prime}(1), i=0,1, \ldots, N_{t}^{\mathrm{d}} \\ & I_{E, C}\left(I_{A, C}\right)>I_{E, V}^{-1}\left(I_{A, V}\right) . \end{array} min such that ∑jρj/jρj≥0∑jρj=1λi=ivi/v′(1),i=0,1,…,NtdIE,C(IA,C)>IE,V−1(IA,V).约束12保证输出为度分布,约束3指定VNs的edge-degree,约束4确保EXIT函数描述的EXIT曲线之前有空隙,确保凸优化问题求解时收敛。
验证:


3.2 改进EEP-LT代码的擦除下限
优化的传统LT代码具有显著的擦除下限,原因
- 存在可变节点low-degree情况(low-degree导致high erasure floor)
- VNs度分布v(x)是渐近泊松分布的,给定VN未连接到任何CN的概率为 e − μ t d e^{-\mu_{t}^{\mathrm{d}}} e−μtd,故解码器erasure probability下限为 e − μ t d e^{-\mu_{t}^{\mathrm{d}}} e−μtd
修改LT编码过程以确保VNs的连接并最大化最小可变节点的度:
度为d的VMs被约束为在当前具有最小度的节点中选择d个不同的VNs。因此,VNs的度要么为 d v d_v dv,要么分布在两个连续的 d v − 1 d_{v−1} dv−1和 d v d_v dv(当编码完成时)。 d v = ⌈ μ t e ⌉ d_{v}=\left\lceil\mu_{t}^{\mathrm{e}}\right\rceil dv=⌈μte⌉.
缺陷:解码器开销增大(需要接受更多的码字才能完成解码)

正则化编码方案的复杂性与传统的LT码相同,因为边数相同。但为了适应所提出的编码方案,需要具有K单元存储器的查找表来跟踪可变节点度。
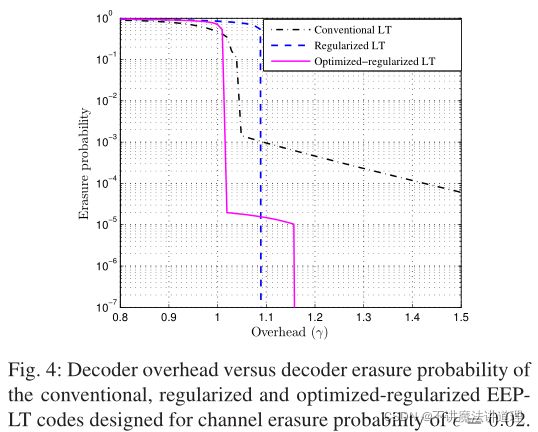
3.3 改进正则化EEP-LT码
既优化解码器开销(通过优化VNs的度分布情况)也最大化可变节点的最小度(改编码器)
4. UEP-LT码的渐近分析
LT码用于unequal erasure protection,首先将K个信息位划分为 r r r类{ s 1 , s 2 , … , s r s_{1}, s_{2}, \ldots, s_{r} s1,s2,…,sr},其尺寸为 α 1 K , α 2 K , … , α r K \alpha_{1} K, \alpha_{2} K, \ldots, \alpha_{r} K α1K,α2K,…,αrK, ∑ j = 1 r α j = 1 \sum_{j=1}^{r} \alpha_{j}=1 ∑j=1rαj=1。其次设置选择从class中选择信息位的概率{ q 1 , q 2 , … , q r q_{1}, q_{2}, \ldots, q_{r} q1,q2,…,qr},保证 w 1 > w 2 > … > w r w_{1}>w_{2}>\ldots>w_{r} w1>w2>…>wr,其中 w j = q j / α i w_{j}=q_{j} / \alpha_i wj=qj/αi。
在第 l l l 次迭代中class j j j中的VNs没有恢复的概率为: P l , j = λ j ( 1 − ρ ( 1 − ∑ k = 1 r q k P l − 1 , k ) ) ≈ e − μ t j d ( ρ ( 1 − ∑ k = 1 r q k P l − 1 , k ) ) \begin{aligned} P_{l, j} &=\lambda_{j}\left(1-\rho\left(1-\sum_{k=1}^{r} q_{k} P_{l-1, k}\right)\right) \\ & \approx e^{-\mu_{t j}^{\mathrm{d}}\left(\rho\left(1-\sum_{k=1}^{r} q_{k} P_{l-1, k}\right)\right)} \end{aligned} Pl,j=λj(1−ρ(1−k=1∑rqkPl−1,k))≈e−μtjd(ρ(1−∑k=1rqkPl−1,k))其中 λ j \lambda_{j} λj为edge-perspective degree distribution,表示VNs的度来自于度为j的CNs的概率, μ t j d = w j μ t d \mu_{t j}^{\mathrm{d}}=w_{j} \mu_{t}^{\mathrm{d}} μtjd=wjμtd表示在class j中VNs的平均度。
在每个类中引入不同的度分布来实现UEP。为了适应每个类中特定的CNs度分布,依照算法1修改了编码过程。为此,引入查找表来跟踪每个类中的可变节点度,使得不同的类对应不同的最小VN度。

补充
解码器擦除概率(decoder erasure probability)定义为通过信息比特总数归一化后的未恢复的信息比特数。
Here the decoder erasure probability is defined as the number of unrecovered information bits normalized by the total number of information bits.
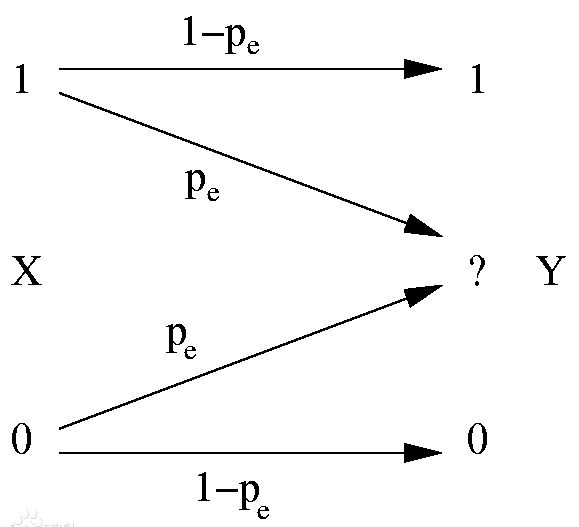
BEC信道中的擦除概率 p e p_e pe是指每一个bit依概率转化为已设定的擦除符号Y