Day 1 数组理论基础 : 704. 二分查找, 35.搜索插入位置, 34. 在排序数组中查找元素的第一个和最后一个位置, 27. 移除元素,
数组理论基础 :
代码随想录
704. 二分查找
题目:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1提示:
- 你可以假设
nums中的所有元素是不重复的。n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。来源:力扣(LeetCode)
链接:704. 二分查找
在数组中找一个target,判断target是否在数组中,如果在,返回数组中对应元素的下标;否则返回-1。同时,题目强调了有序数组和无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件。类似的题目,可以思考二分搜索法。
我比较擅长左闭右闭区间的解法,记录如下:
class Solution(object):
def search(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
tome:O(log n)
space:O(1)
"""
left = 0
right = len(nums) - 1
while(left <= right):
medium = (left + right) // 2
if nums[medium] > target:
right = medium - 1
elif nums[medium] < target:
left = medium + 1
elif nums[medium] == target:
return medium
return -1
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
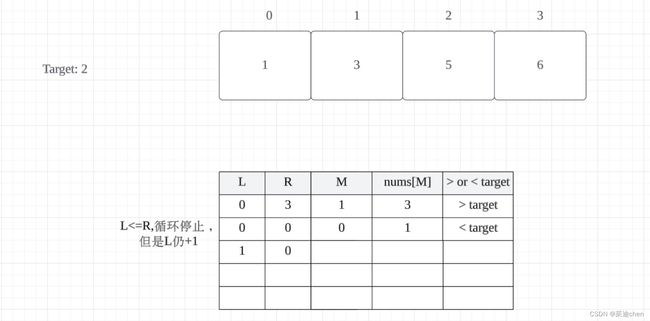
示例 2:输入: nums = [1,3,5,6], target = 2
输出: 1
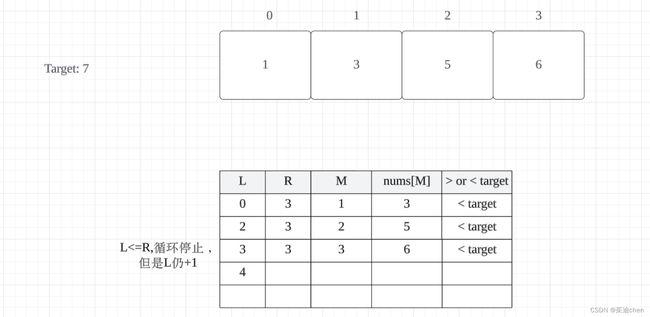
示例 3:输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的 升序 排列数组
-104 <= target <= 104
题目也强调了有序数组和无重复元素,同时题目也明确指出时间复杂度为 O(log n) ,因此可以考虑二分搜索法。
class Solution(object):
def searchInsert(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
time: O(log n)
space: O(1)
"""
# if not nums or nums is None:
# return 0
# for i in range(0,len(nums)):
# if nums[i] >= target:
# return i
# return len(nums) #如果遍历到最后一个位置,还是没有找到nums[i] >= target
if not nums or nums is None:
return 0
left = 0
right = len(nums) - 1
while(left <= right):
medium = (left + right) // 2
if nums[medium] > target:
right = medium - 1
elif nums[medium] < target:
left = medium + 1
else:
return medium
return left可以看到我注释掉的代码,我除刷这道题的时候没有读清楚题意,而选择了时间复杂度为O(n)的解法,是我的失误,下次一定要注意读题!
从这道题可以学到一个重要的概念,即:无论 target 是否存在于数组中,left 最后都会指向 target 应该在的位置,所以我们返回 left。
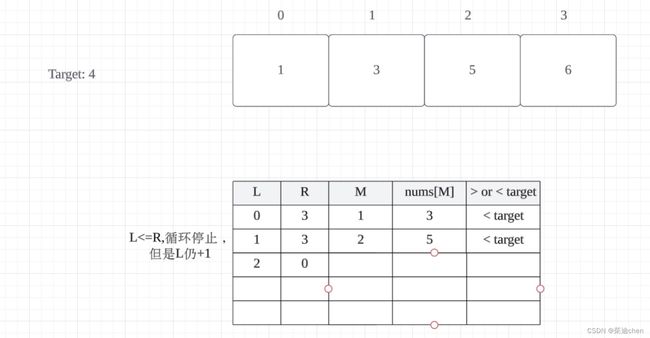
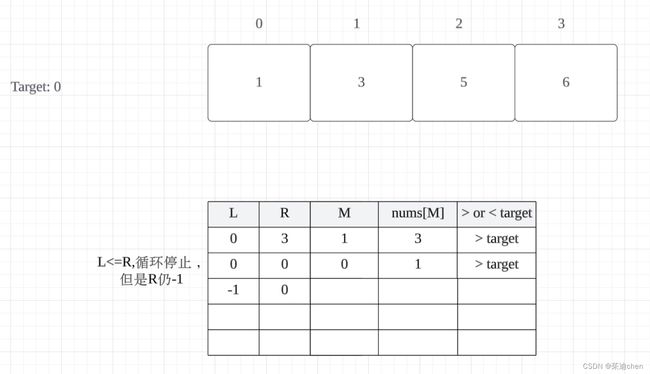
这个原理我想了半天,最后发现还是需要画图,一画图就清晰了:
情况一:
nums[medium] < target:
情况2:
nums[medium] > target:
如果 nums[medium] < target,我们将 left 更新为 medium + 1,这意味着 left 是第一个大于 target 的元素的索引(即 target 应该插入的位置);如果 nums[medium] > target,我们将 right 更新为 medium - 1,这意味着 right 是最后一个小于 target 的元素的索引,所以 target 应该插入到 right + 1 的位置,也就是 left 的位置。
如果 target 存在于数组中,那么 left 和 right 将会收敛到 target 的索引,并且我们最后返回 left 或者 right 就能得到 target 的索引。
因此,无论 target 是否存在于数组中,left 最后都会指向 target 应该在的位置,所以我们返回 left!
34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109
在排序数组中查找元素的第一个和最后一个位置,其实就是找出给定元素的左边界和右边界。由于是排序数组,可以使用二分查找法来优化时间复杂度。首先,我们需要两次使用二分查找,分别找到目标值的起始位置和结束位置。具体代码如下:
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
def findFirst(nums, target):
left, right = 0, len(nums) - 1
while left < right:
mid = (left + right) // 2
if nums[mid] < target:
left = mid + 1
else:
right = mid
return left if nums[left] == target else -1
def findLast(nums, target):
left, right = 0, len(nums) - 1
while left < right:
mid = (left + right + 1) // 2
if nums[mid] > target:
right = mid - 1
else:
left = mid
return left if nums[left] == target else -1
first, last = findFirst(nums, target), findLast(nums, target)
return [first, last] if first <= last else [-1, -1]
27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝
int len = removeElement(nums, val);// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100
这道题的主要的知识点是,数组是存放在连续内存空间上的相同类型数据的集合。删除数组中的元素,并不是单纯的在地理位置上删除该元素,这个位置不能删除,只能覆盖,要将后方的所有元素都向前移动的。因此删除列表中的元素需要 O(n) 的时间。
这道题有两种解法,第一种是暴力解法:
class Solution(object):
def removeElement(self, nums, val):
"""
:type nums: List[int]
:type val: int
:rtype: int
time: O(n^2) 删除列表中的元素需要 O(n) 的时间,所以总的时间复杂度是 O(n^2)。
space: O(1)
"""
if nums is None or not nums:
return 0
for i in range(len(nums) - 1, -1, -1): # 从后向前遍历列表
if nums[i] == val: # 如果找到val
del nums[i] # 删除该元素
return len(nums) # 返回列表的长度,也就是新列表中元素的个数
在找到 val 的时候,删除这个元素并向前移动其后面的所有元素,我们可以倒序遍历列表,这样就不会出现索引错误。
第二种方法是双指针解法:
双指针的策略在编程中是非常实用的,特别是在处理数组或链表这样的线性结构时。以下是一些使用双指针的常见场景:
-
有序数组或链表的查找:当数据是有序的,我们可以使用双指针从两端向中间查找。例如,在已排序的数组中查找两个数使它们的和为给定值。
-
链表操作:在链表中,我们可以使用快慢指针来找到中间元素或检测是否存在环。
-
子序列问题:例如,查找数组中的连续子序列(例如滑动窗口)。
-
数组/链表的反转:使用两个指针,一个在起点,一个在终点,然后两个指针向中间移动并交换元素。
-
去除重复元素:当需要在数组或链表中去除重复元素时,双指针也非常有用,一个指针用于遍历所有元素,另一个指针用于指向已处理过的无重复元素的部分。
双指针的使用是非常灵活的,会根据具体问题有不同的使用方法。总的来说,当你发现通过一次遍历无法解决问题,或者需要维护某种有序或者相对位置关系时,可以考虑是否能通过双指针来解决问题。
我们这道题的双指针,其实就是用一层For循环,解决刚刚暴力解两层For循环做的事情。即用双指针思想帮我们节省了一层For循环的事情。
一般来说我们需要定义一个快指针,定义一个慢指针。
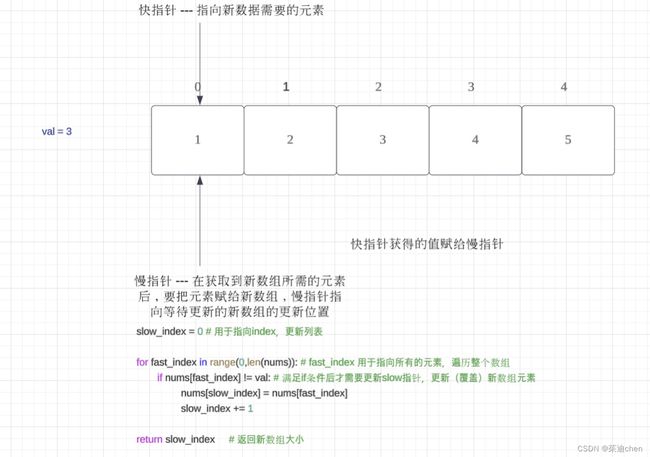
一个快指针用于遍历所有元素,一个慢指针用于指向当前需要替换的位置,当快指针指向的元素不等于 val 时,就将这个元素复制到慢指针的位置,并让慢指针前进一步。用图来形象的表示双指针的思路过程:
其中,if nums[fast_index] != val:
不等的时候才更新慢指针,相等的时候只对快指针++,慢指针不变。由此实现覆盖,快指针的值覆盖慢指针的值。
双指针的代码如下:
class Solution(object):
def removeElement(self, nums, val):
"""
:type nums: List[int]
:type val: int
:rtype: int
time: O(n) 其中n是数组的长度。这是因为我们对数组进行了一次遍历。
space: O(1) 这是因为我们只使用了固定的额外空间,即两个指针和一些临时变量,
而且这个额外空间的大小与输入数组的大小无关。
"""
# 双指针
if nums is None or not nums:
return 0
slow_index = 0 # 用于指向index,更新列表
for fast_index in range(0,len(nums)): # fast_index 用于指向所有的元素,遍历整个数组
if nums[fast_index] != val: # 不等的时候,更新指针数(覆盖)
nums[slow_index] = nums[fast_index]
slow_index += 1
return slow_index