算法：图解递归算法的应用场景和使用途径

什么是递归？

递归就是函数自己调用自己的情况，在二叉树，快排，归并中都有较为广泛的使用场景

使用递归的原因？

当一个问题可以被拆分成无数个子问题，而这些子问题的解决操作全部相同的时候，就可以使用递归

如何理解递归？

• 从宏观上讲，递归是一个宏观的过程，具体表现在：

1. 递归的细节展开图不应过多在意
2. 把递归的函数看成是一个黑盒
3. 相信黑盒可以完成你希望它完成的任务

递归的使用写法

1. 找到相同的子问题
2. 函数体内只写一个子问题的解决方式
3. 找到递归的结束条件

典型例题和分析

汉诺塔问题

汉诺塔问题是非常经典的和递归相关的题，因此花时间进行此题的研究是有意义的，这里使用递归图解分析解决的方法：

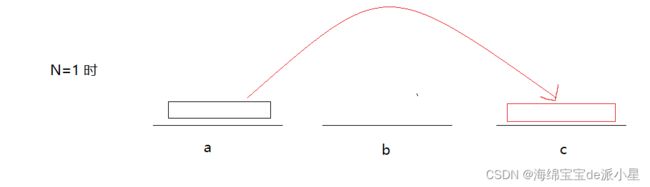
解决递归问题都是从简单问题开始的，假设现在只有一个盘子：

这一步是浅显易懂的，只需要一步即可，如果此时变成两个盘子：

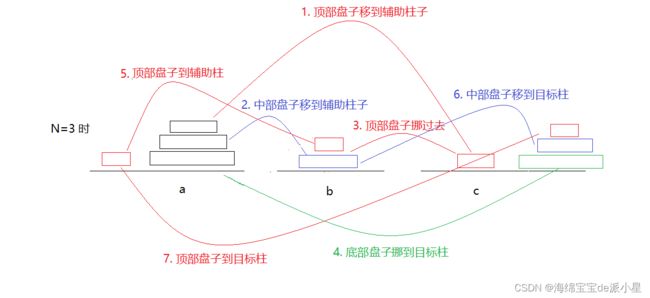
两个盘子的操作分为上面三步，此时还看不出规律，继续找规律：如果变成三个盘子

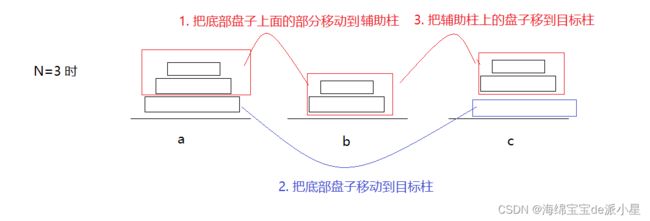
实际上这是有规律可循的，上面的七个步骤其实可以进行一定程度的简化：

是可以简化为下面三步的，而对于上图中的第一步，其实就是当盘子数量为2的时候的情况，因此就找到了规律：当有N个盘子的时候，就让最上面的N-1个盘子移动到辅助柱，让最后一个盘子移动到目标柱，再让N-1个盘子移动到目标柱，而如何把N-1个盘子移动到某个柱子这个操作就可以进入递归进行，因此递归的整体框架就构建出来了

class Solution 
{
public:
    void dfs(vector<int>& a, vector<int>& b, vector<int>& c,int n)
    {
        // 递归终止条件
        if(n==1)
        {
            c.push_back(a.back());
            a.pop_back();
            return;
        }

        // 1.把a上的n-1个盘子借助c移动到b
        dfs(a,c,b,n-1);

        // 2.把a底部移动到目标柱
        c.push_back(a.back());
        a.pop_back();
        
        // 3.把b上的柱子移动到c上
        dfs(b,a,c,n-1);
    }

    void hanota(vector<int>& a, vector<int>& b, vector<int>& c) 
    {
        // dfs中参数的意思：让a柱上的a.size()个盘子借助b柱移动到c柱
        dfs(a,b,c,a.size());
    }
};

合并两个有序链表

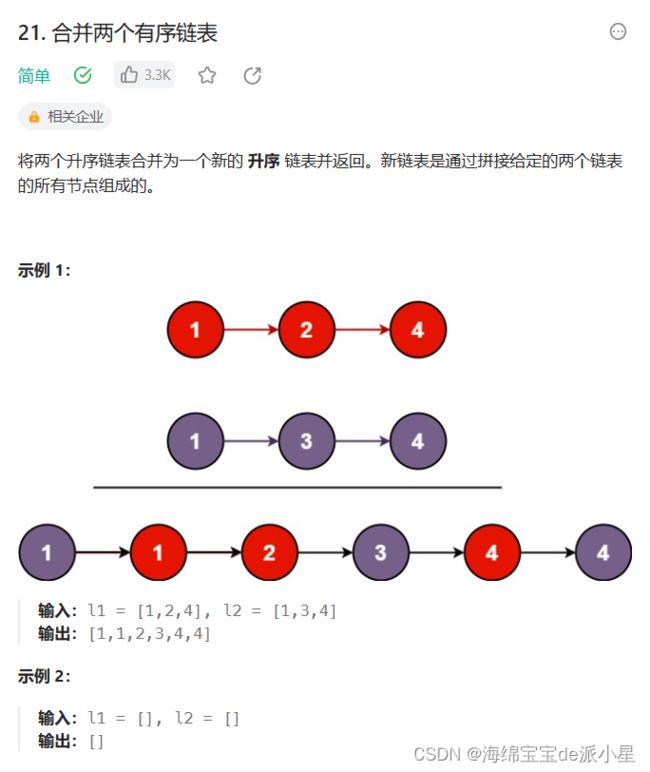
这是链表的经典题目，在之前是使用循环来解决的，实际上这里也可以使用递归来解决

那根据递归的使用条件，首先要找到子问题，从宏观上来讲，这个题的子问题就是，如果list1指向的值大于list2指向的值，就把list1指向的值拿出来，list1->next和list2继续排序，因此这样就找到了递归的子问题循环情况：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution 
{
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) 
    {
        if(list1==nullptr)
        {
            return list2;
        }
        if(list2==nullptr)
        {
            return list1;
        }
        if(list1->val <= list2->val)
        {
            list1->next=mergeTwoLists(list1->next,list2);
            return list1;
        }
        else
        {
            list2->next=mergeTwoLists(list1,list2->next);
            return list2;
        }
    }
};

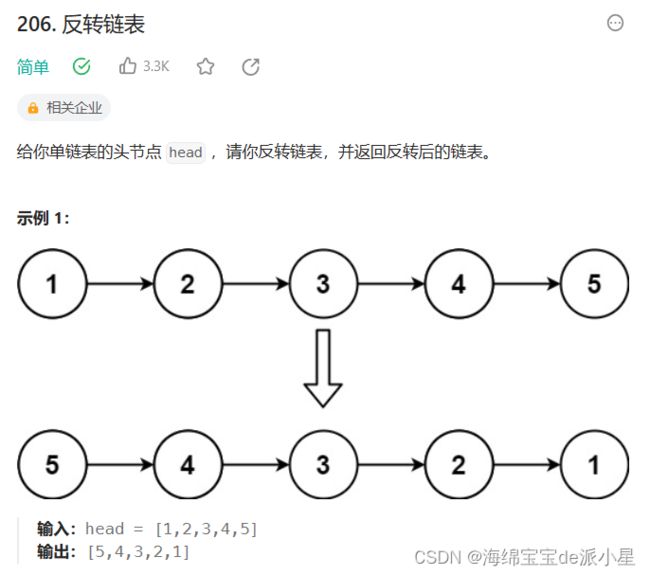
反转链表

这也是链表的一道经典的题目，之前做这个题的时候选择的方法有两种，一种是让上面的链表的每一个节点进行头插，另外一种是让链表的每一个节点模拟这个逆置的过程，总体来说使用头插简单一些

这里使用递归的思想解决问题：

现在要返回的是逆置的链表，因此这里把head之后的部分看成一个整体：

要相信递归可以完成dfs的操作，可以把这些节点都反转过来并且返回新的头结点，我们定义一个newhead进行接收，接着要把头结点和head->next这部分进行一次反转即可

这样看很难理解，但如果换一种角度看，把这个链表想象成一个树，那么就是不断走近树的根，当遇到树的叶子的时候进行返回，从树的叶子开始不断操作，不断的让节点进行反转，其实宏观上讲是一个后序遍历

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution 
{
public:
    ListNode* reverseList(ListNode* head) 
    {
        if(head==nullptr || head->next==nullptr)
        {
            return head;
        }

        ListNode* newhead=reverseList(head->next);

        head->next->next=head;
        head->next=nullptr;

        return newhead;
    }
};

两两交换链表中的节点

传统方法不过多感受，直接迭代即可，可以多定义几个指针就容易写一些

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution 
{
public:
    ListNode* swapPairs(ListNode* head) 
    {
        if(head==nullptr || head->next==nullptr)
        {
            return head;
        }

        ListNode* newhead=new ListNode(0);
        newhead->next=head;
        ListNode* prev=newhead;
        ListNode* slow=prev->next;
        ListNode* fast=slow->next;

        while(slow && fast)
        {
            slow->next=fast->next;
            fast->next=slow;
            prev->next=fast;
            prev=slow;
            slow=prev->next;
            if(slow)
            {
                fast=slow->next;
            }
        }

        return newhead->next;
    }
};

下面重点还是进行递归的方法上：

和上一个题一样，利用递归来解决问题要站在宏观的角度，把除了前两个节点外的节点看成一个整体，讲它交给dfs，此时只需要相信dfs内部一定可以实现目的，可以实现两两交换的目的，再返回一个值，此时只需要把前两个节点和后面的节点连起来即可

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution 
{
public:
    ListNode* swapPairs(ListNode* head) 
    {
        if(head==nullptr || head->next==nullptr)
        {
            return head;
        }

        ListNode* tmp=swapPairs(head->next->next);

        ListNode* next=head->next;
        head->next=tmp;
        next->next=head;
        head=next;

        return head;
    }
};

pow

一个递归实现幂指数的问题，注意递归的结束条件即可

class Solution 
{
public:
    double myPow(double x, int n)
    {
        return n<0 ? 1.0 /pow(x,-(long long)n) : pow(x,n);
    }
    double pow(double x, int n) 
    {
        if(n==0)
        {
            return 1;
        }
        double tmp=pow(x,n/2);
        return n%2==0? tmp*tmp:tmp*tmp*x;
    }
};

总结

• 循环和递归是如何进行的？他们之间有什么相同不同点？

其实不管是循环和递归，都是因为在代码的实现逻辑中出现了一部分内容，需要使用一块相同的逻辑，也就是一个重复的子问题，在这样的条件下就可以使用循环和递归进行

也就是说从某种意义来说，循环和递归是可以相互转换的，只是会涉及到实现难度的问题，比如：
对于要打印N个数，采用循环的方式：

int main()
{
	vector<int> nums{ 1,2,3,4,5,6,7,8,9 };
	for (int i = 0; i < nums.size(); i++)
	{
		cout << nums[i] << " ";
	}
	return 0;
}

也可以采用递归的方式

void print(vector<int>& nums,int i)
{
	if (i == nums.size())
	{
		return;
	}
	cout << nums[i] << " ";
	print(nums, i + 1);
}

int main()
{
	vector<int> nums{ 1,2,3,4,5,6,7,8,9 };
	//for (int i = 0; i < nums.size(); i++)
	//{
	//	cout << nums[i] << " ";
	//}
	print(nums,0);
	return 0;
}

这是对于一些比较简单的情况可以这样相互转换，在大多数情况中，想要实现递归和循环的相互转换不是一件容易的事

• 什么时候用循环？什么时候用递归？

虽然以前从未思考过这些问题，但既然总结到这里就难免有这样的问题

递归和循环的本质的一个区别，其实和递归的展开图有关，对于一个递归的展开图来说，整体上的逻辑其实是对一棵树进行深度优先遍历，这个树有很多种，也许是二叉树也可能是多叉树，但按照逻辑来看递归展开图，每当走到头就返回…实际上这个操作就是一个很明显的深度优先遍历，可能是前序遍历，也可能是后序遍历，这个不是重点，而对于二叉树的遍历，想要将其转换为非递归的模式，虽不是不可以，但也会十分繁琐，因此通俗来讲当有多个分支情况的时候，选取递归来进行遍历是比较合适的

而循环可以看成是只有一条路的树，从头走到尾再返回