Self-Attentive Hawkes Process
#ICML#
今天分享的是ICML 2020的一篇论文《Self-Attentive Hawkes Process》
原文链接:http://proceedings.mlr.press/v119/zhang20q.html?ref=https://githubhelp.com
摘要
捕捉事件发生的动态对于预测下一个事件发生的类型和时间至关重要,解决该问题一种常用的方法是通过霍克斯过程。由于RNN在处理顺序数据,例如语言方面取得了成功,因此目前已经将RNN引入了霍克斯过程。而近几年发现Self-Attention比RNN处理语言的效果更好,所以本研究旨在通过设计一种Self-Attention的霍克斯过程(SAHP)探索自注意力在霍克斯过程中的有效性。
SAHP采用Self-Attention来总结历史事件的影响并计算下一事件的概率。当应用于事件序列时,传统Self-Attention的一个缺陷是其位置编码只考虑序列的顺序,而忽略了事件之间的时间间隔,为了克服这一缺陷,作者通过将时间间隔转换为正弦函数相移的方式,修改了编码。实验表明,SAHP的效果相比于其他模型有所提升,同时,SAHP比基于RNN的模型更易于解释,因为学习到的注意力权重揭示了一种事件类型对另一种类型发生所产生的贡献。
1.介绍
本文的研究目标是根据历史预测下一个事件的类型和发生时间。如下图显示了四种类型的事件和它们的相互影响。这些序列的一个典型的建模问题是预测哪种类型的事件以及事件何时发生。
a图显示的是社交媒体平台上的三个用户的不同类型的行动,填充的形状定义了行动类型,红色箭头表示一个行动对其他行动的影响。b图中单元格 ( i , j ) (i, j) (i,j)的符号对应a图事件类型之间的影响。
2.贡献
① 据作者所知,文章这项工作是第一个将自注意力与霍克斯过程联系起来的。SAHP继承了捕捉复杂动态的改进能力和更高的可解释性。
② 为了考虑事件间的时间间隔,作者提出了一种新颖的时移位置编码,将时间间隔转换为正弦函数的相移。
③ 通过在具有不同序列长度和不同事件类型数量的数据集上的广泛实验,作者证明了SAHP的优越性。
3.算法框架
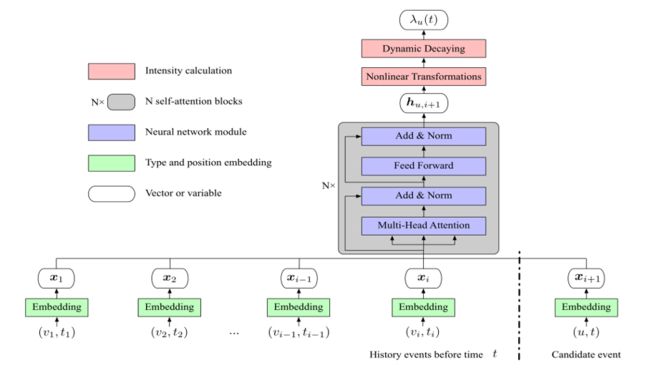
上图为一个事件流和一个事件类型的SAHP架构。整体流程为:先表示出来事件类型的 e m b e d d i n g embedding embedding和位置编码,形成事件的向量。之后通过注意力机制中的多头注意力、残差连接和归一化、前馈全连接网络形成新的向量。最后经过非线性变换和动态衰减形成强度函数。
3.1 事件类型 e m b e d d i n g embedding embedding
输入序列是由事件组成的。为了获得每个事件类型的嵌入,使用了一个线性嵌入层。
t p v = e v W E ( 1 ) tp_v=e_vW_E\ (1) tpv=evWE (1)
公式1的含义是:类型 v v v的 e m b e d d i n g embedding embedding=类型 v v v的独热编码∗嵌入矩阵
3.2 时移的位置编码
上图显示了传统的和新的位置编码如何工作。假设一个事件 ( v i , t i ) (v_i,t_i) (vi,ti)在一个序列的 i = 14 i=14 i=14位置。传统方法将 i = 14 i=14 i=14位置的正弦函数值计算为该事件的位置值,文章的编码修改了这一点,将原来的位置 i i i移到一个新的位置上: i k ′ = i + w k t i ω k {i^{'}_k}=i+\frac{w_kt_i}{\omega_k} ik′=i+ωkwkti。其中 k k k表示嵌入维度。 ω k \omega_k ωk是第 k k k个维度的角度频率, w k w_k wk是一个缩放参数,将时间戳 t i t_i ti转换为第 k k k维的相移。因此,一个序列中的位置被时间 t i t_i ti转移了。
p e ( v i , t i ) k = s i n ( ω k × i + w k × t i ) ( 2 ) pe^k_{(v_i,t_i)}=sin(\omega_k×i+w_k×t_i)\ (2) pe(vi,ti)k=sin(ωk×i+wk×ti) (2)
形成的位置编码如公式2所示。
3.3 历史隐藏向量
由于一个事件由其类型和时间戳组成,作者将位置编码添加到事件类型嵌入中,以获得事件的表示。
x i = t p v + p e k ( 3 ) x_i=tp_v+pe^k\ (3) xi=tpv+pek (3)
公式3的含义是:事件 i i i的表示 x x x=事件类型 e m b e d d i n g embedding embedding+时移的位置编码
3.4 自注意力
获得隐藏向量后,再通过自注意力的方式,计算前一个事件对下一个事件的影响。在此处产生了一个新的向量 h u , i + 1 h_{u,i+1} hu,i+1,总结了以前所有事件的影响。该模块中,在训练期间,需要将时间信息提供给模型,此处通过masking来防止模型获得未来的信息,即通过屏蔽输入序列中与未来事件相对应的值,保证了一个事件的强度仅根据其历史获得。该模块主要包含多头注意力、残差连接和归一化、前馈全连接网络三个部分。
3.5 强度函数
最后通过以下三种非线性变换,基于历史隐向量 h u , i + 1 h_{u,i+1} hu,i+1计算强度函数的三个参数。
μ u , i + 1 = g e l u ( h u , i + 1 W μ ) , \mu_{u,i+1}=gelu(h_{u,i+1}W_\mu) , μu,i+1=gelu(hu,i+1Wμ),
η u , i + 1 = g e l u ( h u , i + 1 W η ) , \eta_{u,i+1}=gelu(h_{u,i+1}W_\eta) , ηu,i+1=gelu(hu,i+1Wη),
γ u , i + 1 = s o f t p l u s ( h u , i + 1 W γ ) . ( 4 ) \gamma_{u,i+1}=softplus(h_{u,i+1}W_\gamma) .\ (4) γu,i+1=softplus(hu,i+1Wγ). (4)
公式4主要用到了两个函数,其中,函数 g e l u gelu gelu代表非线性激活的高斯误差线性单元,函数 s o f t p l u s softplus softplus被用来约束强度函数为正值。
λ u ( t ) = s o f t p l u s ( μ u , i + 1 + ( η u , i + 1 − μ u , i + 1 ) e x p ( − γ u , i + 1 ( t − t i ) ) ) ( 5 ) \lambda_u(t)=softplus(\mu_{u,i+1}+(\eta_{u,i+1}-\mu_{u,i+1})exp(-\gamma_{u,i+1}(t-t_i)))\ (5) λu(t)=softplus(μu,i+1+(ηu,i+1−μu,i+1)exp(−γu,i+1(t−ti))) (5)
公式5是强度函数的定义,这样, t = t i t=t_i t=ti时会有一个起始强度,当 t t t从 t i t_i ti开始增加时,强度以指数形式衰减,并且可以同时捕捉到兴奋和抑制效应。此处的抑制效应指的是当过去的事件降低了未来事件发生的可能性时表现出来的效果。
4.实验
Baselines
- Hawkes Processes (HP):这是最传统的霍克斯过程统计模型
- Recurrent Marked Temporal Point Processes (RMTPP):使用RNN来学习过去事件的影响表示,时间间隔被编码为明确的输入【2016】
- Continuous Time LSTM (CTLSTM):使用连续时间LSTM,不需要将事件间隔编码为LSTM的数字输入【2017】
- Fully Neural Network (FullyNN):用前馈神经网络对累积强度函数进行建模【2019】
- Log Normal Mixture (LogNormMix):通过对数正态混合模型对条件概率密度分布进行建模【2020】
评估指标
- negative log-likelihood (NLL):负对数似然——比较对事件序列建模的能力(NLL 越低,模型对特定事件序列建模的能力就越强)
- 均方根误差 (RMSE)
- Computational efficiency(计算效率):运行时间
- Model interpretability(模型可解释性):第 u 行第 v 列的单元格表示类型 u 分配给类型 v 的统计注意力。
实验结果
① 负对数似然(NLL)

②均方根误差(RMSE)

③ 计算效率

在计算效率的对比中,LogNormMix模型时间最短,SAHP模型处于第二的位置。
5.总结
在本文中,作者提出了一种自注意力的霍克斯过程,其中自注意力被调整以增强强度函数的表达能力。该方法增强了模型预测能力和模型可解释性。


