【文献翻译】KPConv:灵活且可变形的点云卷积
摘要 我们提出了核点卷积(KPConv),一种新的点卷积设计,即在没有任何中间表示的点云上运行。KPConv的卷积权值通过核点在欧氏空间中定位,并应用于核点附近的输入点。它可以使用任意数量的内核点,这使KPConv比固定的网格卷积更灵活。此外,这些位置在空间上是连续的,可以通过网络学习。因此,kpconv可以扩展到可变形的卷积,学习适应核点局部几何。由于有规律的子采样策略,KPConv对于不同的密度也是有效和健壮的。无论是对复杂任务使用可变形的KPConv,还是对简单任务使用刚性的KPConv,我们的网络在多个数据集上都优于先进的分类和分割方法。我们还提供消融研究和可视化,以帮助理解KPConv已经学到了什么,并验证可变形KPConv的描述能力。
1. 引言
深度学习的出现促进了现代计算机视觉的发展,将离散卷积作为其基本构件。该操作将局部邻域的数据合并到2D网格上。由于这种规则结构,它可以在现代硬件上高效地计算,但当失去这种规则结构时,并没有与2D卷积同样效率的卷积运算被正确地定义.
随着3D扫描技术的兴起,许多依赖这种不规则数据的应用程序得到了发展。例如,三维点云分割或三维同步定位和映射依赖于非网格结构数据:点云。点云是三维(或高维)空间中点的集合。在许多应用中,这些点与相应的特征(如颜色)相结合。在本工作中,我们始终将点云视为这两个元素:点P∈RN×3和特征F∈RN×D。这种点云是一种稀疏结构,具有无序的特性,这使得它与网格非常不同。然而,它与定义卷积的网格有一个共同的特性:它是空间局部( spatially localized )的。在网格中,特征通过它们在矩阵中的索引进行定位,而在点云中,特征通过它们对应的点坐标进行定位。因此,将点视为结构元素,将特征视为真实数据。
研究者们已经提出了各种方法来处理这些数据,并且可以将其分组到不同的类别中,我们将在相关工作部分中介绍这些类别。有几种方法属于基于网格的范畴,其原理是将稀疏的三维数据投影到一个规则的结构上,在这个结构上,卷积运算可以更容易地定义[24,29,34]。其他方法采用多层感知器直接处理点云,遵循[49,26]的思想。
最近,有人尝试设计一个直接作用于点的卷积[2,45,20,14,13]。这些方法利用点云的空间定位特性来定义具有空间核的点卷积。他们的想法是,卷积应该定义一组可定制的空间滤波器局部应用于点云。
本文介绍了一种新的点卷积算子核点卷积(Kernal Point Convolution)。KPConv也由一组局部3D滤波器组成,但克服了之前的点卷积限制,如相关工作所示。KPConv受到基于图像的卷积的启发,但是我们使用一组内核点来定义应用每个内核权值的区域,如图1所示。因此,像输入特征一样,核权值由点来携带,它们的影响范围由相关函数定义。内核点的数量不受限制,这使得我们的设计非常灵活。尽管词汇相似,但我们的工作不同于[32],[32]的灵感来自点云配准技术,使用没有任何权值的核点来学习局部几何模式。
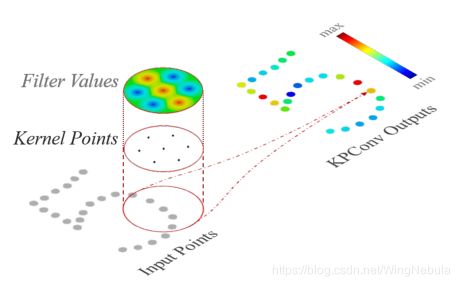
与[41,2,45,20]相反,我们更喜欢半径邻域,而不是KNN。如[13]所示,KNN在非均匀采样设置下是不鲁棒的。我们的卷积对不同密度的鲁棒性是通过结合半径邻域和输入云[38]的规则子采样来保证的。与归一化策略相比[13,14],我们的方法也降低了卷积的计算代价。
在我们的实验部分中,我们展示了KPConv可以用于构建分类和分割的深度架构,同时保持快速的训练和推理时间。总的来说,刚性和可变形的KPConv都表现得很好,在几个数据集上超过了竞争算法。我们发现,严格的KPConv在更简单的任务(如对象分类或小的分割数据集)上取得了更好的性能。可变形的KPConv适用于更困难的任务,比如提供许多对象实例和更大多样性的大型分割数据集。我们还表明,可变形的KPConv对于更少的内核点更健壮,这意味着更强的描述能力。最后,对KPConv ERF的定性研究表明,可变形核提高了网络适应场景对象几何的能力。
2. 相关工作
在这一节中,我们简要回顾以往分析点云的深度学习方法,特别注意与点卷积的定义密切相关的方法。
预测网络 有几个方法指向中间的网格结构。基于图像的网络通常是多视图的,使用一组从点云的不同视角渲染的2D图像[35,4,18]。对于场景分割,这些方法会受到表面遮挡和密度变化的影响。[36]没有选择全局投影视点,而是提出将局部邻域投影到局部切平面,然后用2D卷积进行处理。然而,这种方法很大程度上依赖于切线估计。
在基于体素的方法中,点云被投影到欧几里德空间的三维网格上[24,30,3]。使用像八叉树或哈希映射这样的稀疏结构允许更大的网格和增强的性能[29,9],但这些网络仍然缺乏灵活性,因为它们的内核被限制为使用33= 27或53= 125体素。使用permutohedral lattice代替欧氏格将核减少到15个格子[34],但这个数字仍然受到限制,而KPConv允许任何数量的核点。此外,避免中间结构会使实例掩码检测器或生成模型等更复杂的架构的设计在以后的工作中更加直观。
图卷积网络 在图上的卷积算子的定义已经用不同的方法解决了。一个图上的卷积可以计算为它的谱表示的乘法[8,48],或者它可以聚焦于图所表示的表面[23,5,33,25]。尽管点卷积与最新的图卷积相似[39,43],但后者学习的是边缘关系而不是点的相对位置。换句话说,一个图卷积结合了局部表面补丁的特征,同时对那些补丁在欧几里得空间中的变形保持不变。相反,KPConv根据3D几何图形结合局部特征,从而捕获表面的变形。
点级MLP网络 PointNet[26]被认为是点云深度学习的里程碑。这个网络在每个点上分别使用一个共享的MLP,然后是一个全局的最大池。共享的MLP作为一组学习到的空间编码,输入点云的全局签名计算为每个编码的所有点之间的最大响应。由于没有考虑数据中的局部空间关系,网络的性能受到了限制。继PointNet之后,已经发展了一些层次结构来用mlp聚合局部邻域信息[27,19,21]。
如[41,20,13]所示,点卷积的核可以用MLP实现,因为它可以近似任何连续函数。然而,使用这种表示方式会使卷积算子更加复杂,网络的收敛也更加困难。在我们的例子中,我们定义了一个显式卷积核,就像图像卷积,它的权值是直接学习的,而不需要MLP的中间表示。我们的设计还提供了一个简单的可变形版本,因为偏移量可以直接应用于内核点。
点卷积网络 一些最近的作品也为点定义了显式的卷积内核,但KPConv以独特的设计选择脱颖而出。
Pointwise CNN[14]用体素箱定位核权值,因此缺乏像网格网络那样的灵活性。此外,它们的归一化策略增加了网络不必要的计算量,而KPConv子采样策略减轻了变化的密度和计算量。
SpiderCNN[45]将其核定义为一个多项式函数族,每个相邻函数都有不同的权重。应用于邻居的权重取决于邻居的距离顺序,这使得过滤器在空间上不一致。相比之下,KPConv权值在空间上定位,其结果不随点序变化。
Flex-convolution[10]采用线性函数对其内核进行建模,限制了其代表性。它还使用KNN,它对上述所讨论的密度变化不健壮。
PCNN[2]设计最接近KPConv。它的定义还使用点来携带核权值和相关函数。然而,这种设计是不可扩展的,因为它没有使用任何形式的邻域,使得卷积计算在点的数量上是二次的。此外,它使用高斯相关,其中KPConv使用一个更简单的线性相关,这有助于梯度反向传播时,学习变形[7]。
在实验部分,KPConv网络的性能优于所有可比网络。此外,据我们所知,以前的工作没有一个实验空间变形点卷积。
3. 点卷积网络
3.1 由点定义的核函数
像之前的作品一样,KPConv可以由点卷积(Eq. 1)的一般定义来表达,灵感来自于图像卷积。为清晰起见,我们称 x i x_i xi和 f i f_i fi为来自 P ∈ R N × 3 P∈\mathbb R^{N×3} P∈RN×3的点和来自 F ∈ R N × D F∈\mathbb R^{N×D} F∈RN×D的对应特征。核 g g g在点 x ∈ R 3 x∈\mathbb R^3 x∈R3上的一般点卷积定义 F F F如下: ( F ∗ g ) ( x ) = ∑ x i ∈ N x g ( x i − x ) f i (1) (F*g)(x)=\sum_{x_i \in N_x} {g(x_i-x)f_i} \tag 1 (F∗g)(x)=xi∈Nx∑g(xi−x)fi(1)
我们和[13]一起建议使用半径邻域以确保对不同密度的鲁棒性,因此, N x = { x i ∈ P ∣ ∥ x i − x ∥ ≤ r } N_x=\lbrace x_i \in P| \lVert x_i-x \rVert \leq r\rbrace Nx={xi∈P∣∥xi−x∥≤r},其中 r ∈ R r \in \mathbb R r∈R 是被选中的半径。此外,[38]表明,使用半径邻域计算时,手工制作的3D点特征比使用KNN能有更好地表示。我们认为,对于函数 g g g有一个一致的球面域有助于网络学习有意义的表示。
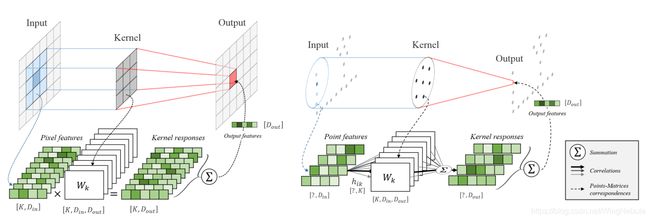
Eq. 1中的关键部分是核函数 g g g的定义,这就是KPConv奇异点所在。 g g g 取以 x x x 为中心的邻域位置作为输入。在下面我们称它们为 y i = x i − x y_i= x_i−x yi=xi−x。由于我们的邻域是由半径 r r r定义的,所以 g g g的定义域是球 B r 3 = { y ∈ R 3 ∣ ∥ y ∥ ≤ r } B^3_r = \lbrace y \in \mathbb R^3 | \lVert y \rVert \leq r\rbrace Br3={y∈R3∣∥y∥≤r}。与图像卷积内核一样(图像卷积与KPConv之间的详细比较见图2),我们希望g对这个域内的不同区域应用不同的权重。在三维空间中定义区域的方法有很多,其中点是最直观的,因为特征也是通过点来定位的。令 { x ~ k ∣ k < K } ⊂ B r 3 \lbrace \tilde{x}_k |k
3.2 刚性核或可变形核(Rigid or Deformable Kernel)
核点位置是卷积算子的关键。我们的刚性核尤其需要定期排列 ( arrange ) 以提高效率。正如我们所说,KPConv的优点之一是它的灵活性,我们需要为任意一个 K K K找到一个规则的配置。我们选择通过解决一个优化问题来放置内核点,其中每个点对其他点施加一个排斥力。这些点被约束在一个有吸引力的球体上,其中一个被约束在中心。我们详细说明了这个过程,并在补充材料中显示了一些规律的配置。最终,将周围的点重新缩放到平均半径 1.5 σ 1.5 \sigma 1.5σ,确保每个核点的影响区域之间有小的重叠和良好的空间覆盖。
有了正确初始化的内核,刚性版本的KPConv是非常有效的,特别是当给定足够大的 K K K来覆盖 g g g的球形域时。然而,它可以通过学习核点位置来增加它的容量。核函数 g g g确实对 x ~ k \tilde{x}_k x~k是可微的,这意味着它们是可学习的参数。我们可以考虑为每个卷积层学习一个全局集合 { x ~ k } \lbrace \tilde{x}_k \rbrace {x~k},但它不会比固定的规则配置带来更强的描述能力。相反,对于每个卷积位置 x ∈ R 3 x∈\mathbb R^3 x∈R3,如[7],网络生成一组 K K K移位 Δ ( x ) \Delta(x) Δ(x),并将可变形的KPConv定义为: ( F ∗ g ) ( x ) = ∑ x i ∈ N x g d e f o r m ( x − x i , Δ ( x ) ) f i (4) (F*g)(x)=\sum_{x_i \in N_x} {g_{deform}(x-x_i, \Delta(x))f_i} \tag 4 (F∗g)(x)=xi∈Nx∑gdeform(x−xi,Δ(x))fi(4) g d e f o r m ( y i , Δ ( x ) ) = ∑ k < K h ( y i , x ~ k + Δ k ( x ) ) W k (5) g_{deform}(y_i, \Delta(x))=\sum_{k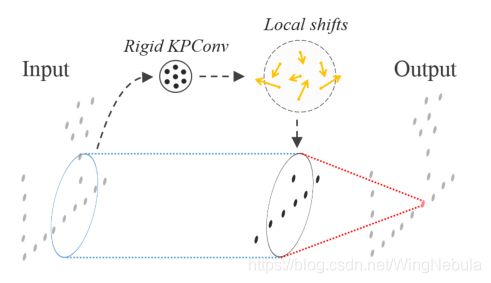
我们将偏移量 Δ k ( x ) \Delta_k(x) Δk(x) 定义为将 D i n D_{in} Din个输入特征映射到 3 K 3K 3K个值的刚性KPConv的输出,如图3所示。在训练过程中,网络同时学习生成位移的刚性核和生成输出特征的可变形核,但第一个学习率设置为全局网络学习率的0.1倍。
不幸的是,这种对图像可变形卷积的直接适应并不适合点云。实际上,核点最终会从输入点中分离出来。这些核点被网络丢失,因为当没有邻居在其影响范围内时,它们的移位的梯度 Δ k ( x ) \Delta_k(x) Δk(x) 为零。关于这些“丢失”的核点的更多细节在补充部分中给出。为了解决这种行为,我们提出了一种“拟合”正则化损失,它惩罚了输入邻居中核点与其最近邻居之间的距离。此外,我们还在所有的影响区域有重叠的核点对之间增加了“排斥”正则化损失,以使它们不会折叠在一起。总的来说,我们对所有卷积位置 x ∈ R 3 x∈\mathbb R^3 x∈R3的正则化损失是: L r e g = ∑ x L f i t ( x ) + L r e p ( x ) (6) \mathcal L_{reg}=\sum_x {\mathcal L_{fit}(x) +\mathcal L_{rep}(x)} \tag 6 Lreg=x∑Lfit(x)+Lrep(x)(6) L f i t = ∑ k < K min y i ( ∥ y i − ( x ~ k + Δ k ( x ) ) ∥ σ ) 2 (7) \mathcal L_{fit}=\sum_{k
3.3 核点网络层(Kernel Point Network Layers)
本节将说明如何将KPConv理论有效地付诸实践。为了获得更多细节,我们已经使用Tensorflow库发布了我们的代码。
处理不同密度的子采样 如引言所述,我们使用子采样策略来控制每一层输入点的密度。为了保证点采样位置的空间一致性,我们倾向于网格子采样。因此,每一层的支撑点都携带着特征位置,作为所有非空网格中包含的原始输入点的重心。
池化层 为了创建具有多层尺度的架构,我们需要逐步减少点的数量。由于我们已经有了网格子采样,我们在每个池化层将cell的大小增加了一倍,和其他相关参数一起,逐渐增加KPConv的感受野。在每个新位置汇集的特性可以通过max-pooling或KPConv获得。我们在我们的体系结构中使用后者,并将其称为“strided KPConv”,类似于图像strided卷积。
KPConv层 我们的卷积层将点 P ∈ R N × 3 P \in \mathbb R^{N \times 3} P∈RN×3、它们对应的特征 F ∈ R N × D i n F \in \mathbb R^{N \times D_{in}} F∈RN×Din 和邻域索引矩阵 n ∈ [ 1 , N ] N ′ × n m a x n \in [1, N]^{N' \times n_{max}} n∈[1,N]N′×nmax 作为输入。 N ′ N' N′ 是计算邻域的位置的数量,可以不同于 N N N(在“strided”KPConv的情况下)。邻域矩阵必须有最大邻域的大小 n m a x n_{max} nmax。因为大多数邻域包含小于 n m a x n_{max} nmax 的邻域,因此矩阵 n n n 包含未使用的元素。我们称它们为阴影邻域,它们在卷积计算中被忽略。
网络参数 每一个层 j j j 都有一个cell size (单元格大小) d l j dl_j dlj,我们可以从中推断出其他参数。设置核点影响距离为 σ j = Σ × d l j \sigma _j=\Sigma \times dl_j σj=Σ×dlj。对于刚性KPConv,当平均核点半径为 1.5 σ j 1.5 \sigma _j 1.5σj 时,卷积半径自动设置为 2.5 σ j 2.5 \sigma _j 2.5σj 。对于可变形的KPConv,可以选择 r j = ρ × d l j r_j=\rho \times dl_j rj=ρ×dlj 的卷积半径。 Σ \Sigma Σ 和 ρ \rho ρ 是为整个网络设置的比例系数。除非另有说明,我们将在所有实验中使用以下通过交叉验证选择的参数: K = 15 , Σ = 1.0 , ρ = 5.0 K=15, \Sigma =1.0, \rho=5.0 K=15,Σ=1.0,ρ=5.0。第一个子采样单元格大小 d l 0 dl_0 dl0 将依赖于数据集,并且,如上所述, d l j + 1 = 2 ∗ d l j dl_{j+1} = 2*dl_j dlj+1=2∗dlj。
3.4 核点网络结构(Kernel Point Network Architectures)
结合类比与成功的图像网络和实证研究,我们设计了两种网络架构用于分类和分割任务。详细说明这两种架构的图表可以在补充材料中找到。
KP-CNN是一个5层分类卷积网络。每一层包含两个卷积块,除第一层外,其他层的的第一个卷积块被 strided。我们的卷积块设计类似 bottleneck ResNet[12],用KPConv代替图像卷积,使用了批处理归一化和有漏洞的ReLu激活(leaky ReLu activation)。在最后一层之后,特征被全局平均池化聚合,并由完全连接层和softmax层进行处理,就像在图像CNN中一样。对于可变形KPConv的结果,我们只在最后5个KPConv块中使用可变形内核(参见补充材料中的架构细节)。
KP-FCNN是一个用于分割的全卷积网络。编码器部分与KP-CNN相同,解码器部分使用最近的上采样来获得最终的逐点特征。跳跃链接用于在编码器和解码器的中间层之间传递特性。这些特征被连接到上采样的特征,并通过单个卷积进行处理,这相当于图像中的1×1卷积或PointNet中的共享MLP。可以用KPConv替换最近的上采样操作,方法与strided KPConv相同,但它不会导致性能的显著改善。
4. 实验
4.1 三维形状分类与分割
数据 首先,我们在两个公共模型数据集上评估我们的网络。我们使用ModelNet40[44]进行分类,使用ShapenetPart[47]进行部分分割。ModelNet40包含来自40个类别的12,311个网格CAD模型。ShapenetPart是来自16个类别的16681个点云的集合,每个点云都有2-6个部件标签。为了进行基准测试,我们使用[27]提供的数据。在这两种情况下,我们都遵循标准的训练/测试分割和缩放对象,使其适合于一个单位球面(并在本实验的其余部分将单位视为米)。我们忽略了正态线,因为它们只能用于人工数据。
分类任务 我们将第一个子采样网格大小设置为 d l 0 = 2 c m dl_0=2cm dl0=2cm。我们没有添加任何特征作为输入;每个输入点被赋予一个等于1的常数特征,而不是可以认为是0的空空间。这个常量特征对输入点的几何形状进行编码。像[2]一样,我们的数据增广过程包括缩放、翻转和扰动这些点。在这个设置中,我们能够在Nvidia Titan Xp上每秒处理 2.9 个 batches 的 16 个点云。由于我们的子采样策略,并不是所有的输入点云都有相同的点数,这不是一个问题,因为我们的网络接受可变的输入点云大小。在我们的框架中,ModelNet40对象点云平均包含6800个点。其他训练参数在补充材料中有详细说明,以及架构细节。我们还包括刚性和可变形KPConv的参数数量和训练/推理速度。
如表1所示,我们的网络比只使用点的其他先进方法性能更好(我们不考虑使用法线作为额外输入的方法)。我们还注意到,刚性 KPConv 性能要好一些。我们认为这可以用任务的简单性来解释。如果可变形内核增加了更多的描述能力,那么它们同时也增加了整个网络的复杂性,这可能会干扰收敛,或导致对形状分类等简单任务的过拟合。
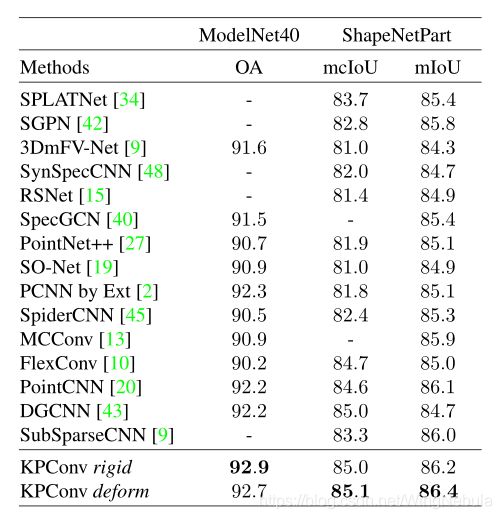
分割任务 对于这个任务,我们使用与分类任务相同的参数的 KP-FCNN 架构,将位置 ( x , y , z ) (x, y, z) (x,y,z) 作为常量1的附加特征,并使用相同的增强过程。我们训练一个有多个 head 的网络来分割每个对象类的部分。云更小了(平均2300点),我们每秒可以处理大小为 16 个形状的 4.1 个 batches。表1显示了实例平均 mIoU 和类 mIoU。我们在补充材料中详细说明了每个类mIoU。KP-FCNN优于所有其他算法,包括那些使用额外输入(如图像或法线)的算法。形状分割是一项比形状分类更困难的任务,我们可以看到KPConv在可变形内核下有更好的性能。
4.2 三维场景分割
数据 我们的第二个实验显示了我们的分割架构如何推广到真实的室内和室外数据。为此,我们选择在4个不同性质的数据集上测试我们的网络。用于室内杂乱场景的Scannet[6],用于室内大空间的S3DIS[1],用于室外固定扫描的Semantic3D[11],以及用于室外移动扫描的Paris-Lille-3D[31]。Scannet包含1513个小训练场景和100个用于在线基准测试的测试场景,全部标注了20个语义类。S3DIS覆盖了三个不同建筑的六个大型室内区域,共有13个类别,总计2.73亿点。和[37]一样,我们主张使用Area-5作为测试场景,以更好地衡量我们的方法的泛化能力。Semantic3D是一个在线基准测试,包括对不同户外场景的几个固定激光雷达扫描。该数据集用8个类标注了40多亿个点,但它们大多覆盖了地面、建筑或植被,对象实例比其他数据集要少。我们倾向于减少8挑战,因为它更少的偏向于靠近扫描仪的物体。巴黎-里尔3d包含4个不同城市超过2公里的街道,也是一个在线基准。这个数据集的1.6亿个点用10个语义类标注。
用于真实场景分割的pipeline 这些数据集中的3D场景太大,无法分割为一个整体。我们的KP-FCNN架构用于分割球体中包含的小子云。训练时,球是在场景中随机挑选的。在测试中,我们定期在点云中选择球体,但确保每个点被不同的球体位置测试多次。就像在模型数据集上的投票方案一样,每个点的预测概率都是平均的。当数据集被着色时,我们使用这三个颜色通道作为特征。我们仍然使用常量特征1,以确保黑色/暗点不会被忽略。对于我们的卷积,一个所有特征都等于0的点就等于空空间。输入球半径选择为 50 × d l 0 50 \times dl_0 50×dl0 (参照Modelnet40实验)。
结果 由于室外物体大于室内物体,我们在 Semantic3D 和 Paris-Lille3D 上使用 d l 0 = 6 c m dl_0=6cm dl0=6cm,在 Scannet 和 S3DIS 上使用 d l 0 = 4 c m dl_0=4cm dl0=4cm。如表2所示,我们的体系结构在 Scannet 上排名第二,并且在其他数据集上优于所有其他分割体系结构。与其他点卷积架构相比[2,20,41],KPConv 在 Scannet 上的性能比以前提高了 19 个 mIoU 点,在 S3DIS 上提高了 9 个 mIoU 点。他们的原始论文[9]中没有报道 SubSparse CNN 在 Scannet 上的评分,所以在不知道他们实验设置的情况下很难进行比较。我们可以注意到,在 ShapeNetPart 分割的相同实验设置中,KPConv 的表现比 SubSparse CNN 高出近 2 mIoU 点。

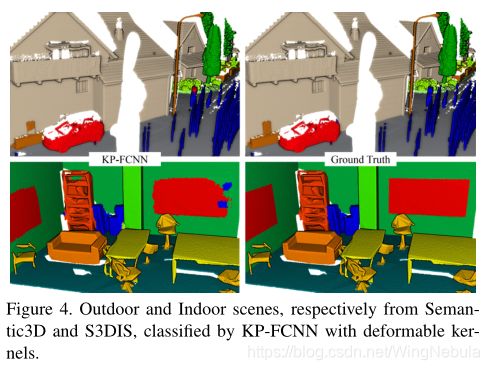
在这4个数据集中,KPConv 可变形内核在 Paris-Lille-3D 和 S3DIS 上的结果更好,而刚性版本在 Scannet 和 Semantic3D 上的结果更好。如果我们遵循我们的假设,我们可以通过该数据集缺乏多样性来解释 Semantic3D 的较低分数。事实上,尽管包含15个场景和40亿个点,它包含了大部分的地面、建筑和植被点,以及一些真实的物体,如汽车或行人。扫描网络由1500多个不同物体和形状的场景组成,虽然不是这样,我们的验证研究并没有反映在这个基准的测试分数上。我们发现,在几个不同的验证集上,可变形的KPConv优于刚性的对应对象(见第4.3节)。结论是,这些结果表明,可变形KPConv的描述能力对网络在大型和多样的数据集上是有用的。我们相信KPConv可以在更大的数据集上蓬勃发展,因为它的内核结合了强大的描述能力(相比于其他更简单的表示,如[10]的线性内核)和强大的可学习性(MLP卷积的权重,如[20,41]是更复杂的学习)。图4显示了Semantic3D和S3DIS上的场景分割示意图。更多的结果可视化在补充材料中提供。
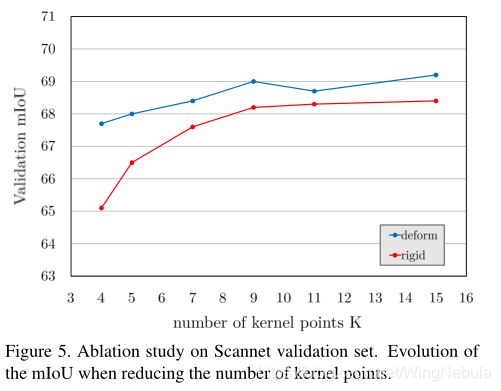
4.3 消融研究
我们进行了一项消融研究来支持我们的主张,即变形KPConv比刚性KPConv具有更强的描述性。这个想法是通过阻碍网络的能力,来揭示可变形内核的真正潜力。我们使用Scannet数据集(与以前相同的参数)并使用正式的验证集,因为测试集不能用于此类评估。如图5所示,当限制为4个内核点时,可变形的KPConv只损失1.5%的mIoU。在相同的配置中,刚性KPConv损失3.5% mIoU。
正如第4.2节所述,我们还可以看到,具有15个内核点的可变形KPConv比刚性KPConv性能更好。虽然在测试集上不是这样,但我们尝试了不同的验证集,以确认可变形KPConv的优越性能。这并不奇怪,因为我们在S3DIS上得到了相同的结果。可变形的KPConv似乎在室内数据集上很受欢迎,这比室外数据集提供了更多的多样性。为了理解原因,我们需要超越数字,看看KPConv的两个版本有效地学习了什么。
4.4 习得特征和有效接受域
为了更深入地理解KPConv,我们提供了关于学习机制的两个见解。
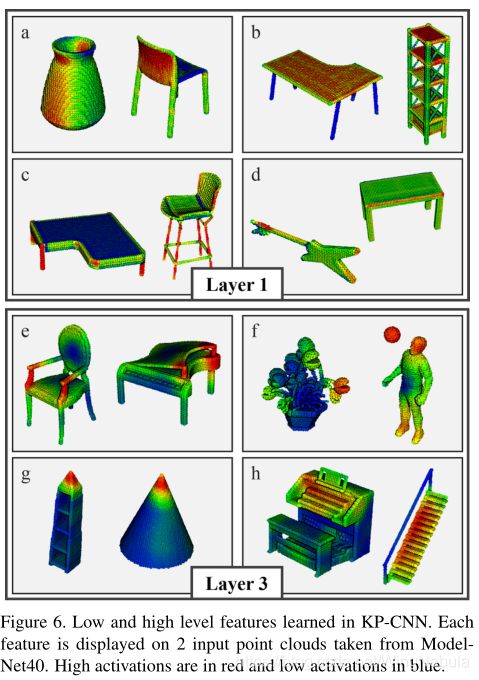
习得特征 我们的第一个想法是将我们的网络学到的特征形象化。在这个实验中,我们在ModelNet40上使用刚性KPConv训练KP-CNN。我们在垂直轴上增加了随机旋转以增加输入形状的多样性。然后,我们将每个学习到的特征可视化,根据它们对该特征的激活程度着色点。在图6中,我们在第一层和第三层选择了最大化激活不同特征的输入点云。为了更干净的显示,我们从层的下采样点投影激活到原始输入点。我们观察到,在第一层中,网络能够学习低级特征,如垂直/水平面(a/b)、线性结构©或角落(d)。在后面的一层中,网络能够检测更复杂的形状,如小扶壁(e)、球(f)、锥体(g)或楼梯(h)。很难看到刚性和可变形KPConv之间的区别。这个工具对于理解KPConv通常可以学到什么非常有用,但是我们需要另一个工具来比较两个版本。
有效接受域 为了理解刚性和变形KPConv学习的表征之间的差异,我们可以计算其不同位置的有效接受域[22]。ERF是对每个输入点在特定位置上对KPConv层结果的影响的度量。它计算为KPConv响应在这个特定位置相对于输入点特征的梯度。正如我们在图7中所看到的,ERF的变化取决于以它为中心的对象。我们看到,严格的KPConv ERF对每种类型的对象都有一个相对一致的范围,而可变形的KPConv ERF似乎适应对象的大小。事实上,它覆盖了整个床,并且更多地集中在椅子上,而不是周围的地面上。当在一个平面上居中时,它似乎也忽略了大部分,并在场景中获取更多的细节。这种自适应行为表明,可变形的KPConv提高了网络对场景对象几何形状的适应能力,并解释了其在室内数据集上的更好性能。

5. 结论
在这项工作中,我们提出KPConv,一种处理点云的卷积。KPConv以半径邻域为输入,通过一小组核点在空间上定位权值对其进行处理。我们定义了这个卷积算子的变形版本,它可以有效地学习局部位移,使卷积核适应点云几何。根据数据集的多样性,或选择的网络配置,可变形和刚性的KPConv都是有价值的,我们的网络为几乎每个测试数据集带来了新的最先进的性能。我们发布了我们的源代码,希望有助于进一步研究点云卷积架构。除了提出的分类和分割网络外,KPConv还可以用于cnn处理的任何其他应用。我们认为,变形卷积可以在更大的数据集或具有挑战性的任务中蓬勃发展,如目标检测、激光雷达流计算或点云补全。
参考文献
[1] Iro Armeni, Ozan Sener, Amir R. Zamir, Helen Jiang, Ioannis Brilakis, Martin Fischer, and Silvio Savarese. 3d semantic parsing of large-scale indoor spaces. InProceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1534–1543, 2016. http:// buildingparser.stanford.edu/ dataset.html.
[2] Matan Atzmon, Haggai Maron, and Yaron Lipman. Point convolutional neural networks by extension operators. ACM Transactions on Graphics (TOG), 37(4):71, 2018.
[3] Yizhak Ben-Shabat, Michael Lindenbaum, and Anath Fischer. 3dmfv: Three-dimensional point cloud classification in real-time using convolutional neural networks. IEEE Robotics and Automation Letters, 3(4):3145–3152, 2018.
[4] Alexandre Boulch, Bertrand Le Saux, and Nicolas Audebert. Unstructured point cloud semantic labeling using deep segmentation networks. In Proceedings of the Workshop on 3D Object Retrieval (3DOR), 2017.
[5] Michael M. Bronstein, Joan Bruna, Yann LeCun, Arthur Szlam, and Pierre V andergheynst. Geometric deep learning: going beyond euclidean data. IEEE Signal Processing Magazine, 34(4):18–42, 2017.
[6] Angela Dai, Angel X. Chang, Manolis Savva, Maciej Halber, Thomas Funkhouser, and Matthias Nießner. Scannet: Richly-annotated 3d reconstructions of indoor scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5828–5839, 2017. http://kaldir.vc.in.tum.de/ scannet benchmark.
[7] Jifeng Dai, Haozhi Qi, Y uwen Xiong, Yi Li, Guodong Zhang, Han Hu, and Yichen Wei. Deformable convolutional networks. In Proceedings of the IEEE international Conference on Computer Vision, pages 764–773, 2017.
[8] Michaël Defferrard, Xavier Bresson, and Pierre V andergheynst. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in Neural Information Processing Systems, pages 3844–3852, 2016.
[9] Benjamin Graham, Martin Engelcke, and Laurens van der Maaten. 3d semantic segmentation with submanifold sparse convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 9224–9232, 2018.
[10] Fabian Groh, Patrick Wieschollek, and Hendrik P .A. Lensch. Flex-convolution. In Asian Conference on Computer Vision, pages 105–122. Springer, 2018.
[11] Timo Hackel, Nikolay Savinov, Lubor Ladicky, Jan D. Wegner, Konrad Schindler, and Marc Pollefeys. Semantic3d.net: A new large-scale point cloud classification benchmark. arXiv preprint arXiv:1704.03847, 2017. http:// www.semantic3d.net.
[12] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pages 770–778, 2016.
[13] Pedro Hermosilla, Tobias Ristchel, Pere-Pau Vázquez, Álvaro Vinacua, and Timo Ropinski. Monte carlo convolution for learning on non-uniformly sampled point clouds. ACM Transactions on Graphics (TOG), 37(6):235–1, 2018.
[14] Binh-Son Hua, Minh-Khoi Tran, and Sai-Kit Yeung. Point-wise convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 984–993, 2018.
[15] Qiangui Huang, Weiyue Wang, and Ulrich Neumann. Recurrent slice networks for 3d segmentation of point clouds. In Proceedings of the IEEE Conference on Computer Vision
and Pattern Recognition, pages 2626–2635, 2018.
[16] Roman Klokov and Victor Lempitsky. Escape from cells: Deep kd-networks for the recognition of 3d point cloud models. In Proceedings of the IEEE International Conference on
Computer Vision, pages 863–872, 2017.
[17] Loic Landrieu and Martin Simonovsky. Large-scale point cloud semantic segmentation with superpoint graphs. In Proceedings of the IEEE Conference on Computer Vision and
Pattern Recognition, pages 4558–4567, 2018.
[18] Felix Järemo Lawin, Martin Danelljan, Patrik Tosteberg, Goutam Bhat, Fahad Shahbaz Khan, and Michael Felsberg. Deep projective 3d semantic segmentation. In International
Conference on Computer Analysis of Images and Patterns, pages 95–107. Springer, 2017.
[19] Jiaxin Li, Ben M. Chen, and Gim Hee Lee. So-net: Self-organizing network for point cloud analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern
Recognition, pages 9397–9406, 2018.
[20] Yangyan Li, Rui Bu, Mingchao Sun, Wei Wu, Xinhan Di, and Baoquan Chen. Pointcnn: Convolution on x-transformed points. In Advances in Neural Information Processing Sys-
tems, pages 820–830, 2018.
[21] Xinhai Liu, Zhizhong Han, Y u-Shen Liu, and Matthias Zwicker. Point2sequence: Learning the shape representation of 3d point clouds with an attention-based sequence to sequence network. arXiv preprint arXiv:1811.02565, 2018.
[22] Wenjie Luo, Y ujia Li, Raquel Urtasun, and Richard Zemel. Understanding the effective receptive field in deep convolutional neural networks. In Advances in neural information processing systems, pages 4898–4906, 2016.
[23] Jonathan Masci, Davide Boscaini, Michael Bronstein, and Pierre Vandergheynst. Geodesic convolutional neural networks on riemannian manifolds. In Proceedings of the IEEE international conference on computer vision work- shops, pages 37–45, 2015.
[24] Daniel Maturana and Sebastian Scherer. Voxnet: A 3d convolutional neural network for real-time object recognition. In Intelligent Robots and Systems (IROS), 2015 IEEE/RSJ International Conference on, pages 922–928. IEEE, 2015.
[25] Federico Monti, Davide Boscaini, Jonathan Masci, Emanuele Rodola, Jan Svoboda, and Michael M. Bronstein. Geometric deep learning on graphs and manifolds using mixture model cnns. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5115–5124, 2017.
[26] Charles R. Qi, Hao Su, Kaichun Mo, and Leonidas J. Guibas. Pointnet: Deep learning on point sets for 3d classification andsegmentation. InProceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 652–660,2017.
[27] Charles R. Qi, Li Yi, Hao Su, and Leonidas J. Guibas. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Advances in Neural Information Processing Systems, pages 5099–5108, 2017.
[28] Dario Rethage, Johanna Wald, Jurgen Sturm, Nassir Navab, and Federico Tombari. Fully-convolutional point networks for large-scale point clouds. In Proceedings of the European Conference on Computer Vision (ECCV), pages 596–611, 2018.
[29] Gernot Riegler, Ali Osman Ulusoy, and Andreas Geiger. Octnet: Learning deep 3d representations at high resolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, volume 3, 2017.
[30] Xavier Roynard, Jean-Emmanuel Deschaud, and Franc, ois Goulette. Classification of point cloud scenes with multi-scale voxel deep network. arXiv preprint arXiv:1804.03583, 2018.
[31] Xavier Roynard, Jean-Emmanuel Deschaud, and Franc, ois Goulette. Paris-lille-3d: A large and high-quality ground-truth urban point cloud dataset for automatic segmentation and classification. The International Journal of Robotics Research, 37(6):545–557, 2018. http:// npm3d.fr.
[32] Yiru Shen, Chen Feng, Yaoqing Yang, and Dong Tian. Mining point cloud local structures by kernel correlation and graph pooling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, volume 4, 2018.
[33] Martin Simonovsky and Nikos Komodakis. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 3693–3702, 2017.
[34] Hang Su, V arun Jampani, Deqing Sun, Subhransu Maji, Evangelos Kalogerakis, Ming-Hsuan Yang, and Jan Kautz. Splatnet: Sparse lattice networks for point cloud processing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2530–2539, 2018.
[35] Hang Su, Subhransu Maji, Evangelos Kalogerakis, and Erik Learned-Miller. Multi-view convolutional neural networks for 3d shape recognition. In Proceedings of the IEEE International Conference on Computer Vision, pages 945–953, 2015.
[36] Maxim Tatarchenko, Jaesik Park, Vladlen Koltun, and QianYi Zhou. Tangent convolutions for dense prediction in 3d. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 3887–3896, 2018.
[37] Lyne Tchapmi, Christopher Choy, Iro Armeni, JunYoung Gwak, and Silvio Savarese. Segcloud: Semantic segmentation of 3d point clouds. In 2017 International Conference on 3D Vision (3DV), pages 537–547. IEEE, 2017.
[38] Hugues Thomas, Franc ¸ois Goulette, Jean-Emmanuel Deschaud, and Beatriz Marcotegui. Semantic classification of 3d point clouds with multiscale spherical neighborhoods. In 2018 International Conference on 3D Vision (3DV), pages 390–398. IEEE, 2018.
[39] Nitika V erma, Edmond Boyer, and Jakob V erbeek. Feastnet: Feature-steered graph convolutions for 3d shape analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2598–2606, 2018.
[40] Chu Wang, Babak Samari, and Kaleem Siddiqi. Local spectral graph convolution for point set feature learning. In Proceedings of the European Conference on Computer Vision (ECCV), pages 52–66, 2018.
[41] Shenlong Wang, Simon Suo, Wei-Chiu Ma, Andrei Pokrovsky, and Raquel Urtasun. Deep parametric continuous convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2589–2597, 2018.
[42] Weiyue Wang, Ronald Y u, Qiangui Huang, and Ulrich Neumann. SGPN: Similarity group proposal network for 3d point cloud instance segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2569–2578, 2018.
[43] Yue Wang, Y ongbin Sun, Ziwei Liu, Sanjay E. Sarma, Michael M. Bronstein, and Justin M. Solomon. Dynamic graph cnn for learning on point clouds. ACM Transactions on Graphics (TOG), 2019.
[44] Zhirong Wu, Shuran Song, Aditya Khosla, Fisher Y u, Linguang Zhang, Xiaoou Tang, and Jianxiong Xiao. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pages 1912–1920, 2015.
[45] Yifan Xu, Tianqi Fan, Mingye Xu, Long Zeng, and Y u Qiao. Spidercnn: Deep learning on point sets with parameterized convolutional filters. In Proceedings of the European Conference on Computer Vision (ECCV), pages 87–102, 2018.
[46] Xiaoqing Ye, Jiamao Li, Hexiao Huang, Liang Du, and Xiaolin Zhang. 3d recurrent neural networks with context fusion for point cloud semantic segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), pages 415–430. Springer, 2018.
[47] Li Yi, Vladimir G. Kim, Duygu Ceylan, I Shen, Mengyan Yan, Hao Su, Cewu Lu, Qixing Huang, Alla Sheffer, Leonidas J. Guibas, et al. A scalable active framework for region annotation in 3d shape collections. ACM Transactions on Graphics (TOG), 35(6):210, 2016.
[48] Li Yi, Hao Su, Xingwen Guo, and Leonidas J. Guibas. SyncspecCNN: Synchronized spectral cnn for 3d shape segmentation. In CVPR, pages 6584–6592, 2017.
[49] Manzil Zaheer, Satwik Kottur, Siamak Ravanbakhsh, Barnabas Poczos, Ruslan R. Salakhutdinov, and Alexander J Smola. Deep sets. In Advances in Neural Information Processing Systems, pages 3391–3401, 2017.
[50] Chris Zhang, Wenjie Luo, and Raquel Urtasun. Efficient convolutions for real-time semantic segmentation of 3d point clouds. In 2018 International Conference on 3D Vision(3DV), pages 399–408. IEEE, 2018.