【GAMES101】Lecture07-09 Shading 精要
【GAMES101】Lecture07-09 Shading 精要
-
-
- Definitions
- Blinn-Phong Reflection Model
-
- Ambient Term
- Diffuse Term
- Speculator Term
- Shading Frequencies
-
- 1. Flat shading - Shade each triangle
- 2. Gouraud shading - Shade each vertex
- 3. Phong shading - Shade each pixel
-
- 重心坐标
- 三种shading model的比较与选择
- Graphics Pipeline(Real-time Rendering)
-
- 1. Vertex Processing AND Triangle Processing
- 2. Rasterization
- 3. Fragment Processing
- 4. Framebuffer Operations
- Shading涉及的流程
- Texture
-
- Texture Mapping
- Applying Textures
- Problems in Simple Texture Mapping
-
- 1. 纹理过小 - Texture Magnification(纹理放大)
- 2. 纹理过大 - Texture Minification(纹理缩小)
-
- Solution:Mipmap - fast, approximate, square Range Queries
- Mipmap局限
- Applications of textures
-
- 1. 环境贴图/光照 Environment Map/Lighting
- 2. 不表示颜色的贴图 —— 高度/法线贴图
- 3. 纹理的其他应用
-
- 3D程序纹理
- 预先计算 - 环境光遮蔽
- 体渲染
-
本文图片来源于GAMES101课件。
目前已经完成的流程:模型变换 → \rightarrow →视图变换 → \rightarrow →视口变换 → \rightarrow →光栅化。

然而,目前得到的图像并不真实,比如下面左边的图,而实际上我们希望看到右边这样的结果,这是因为我们还没有进行着色(Shading)。


Definitions
Shading : = := := The process of applying a material to an object.
Material : = := :=物体的材质,如玻璃、木质、金属等,不同材质与光线的作用效果不同。
Shading Point : = := :=着色点,无论所在面是曲面还是平面,在着色点局部非常小的位置都可以视为一个小平面,着色点的值即着色结果,它取决于多个因素,可以表示为如下函数。
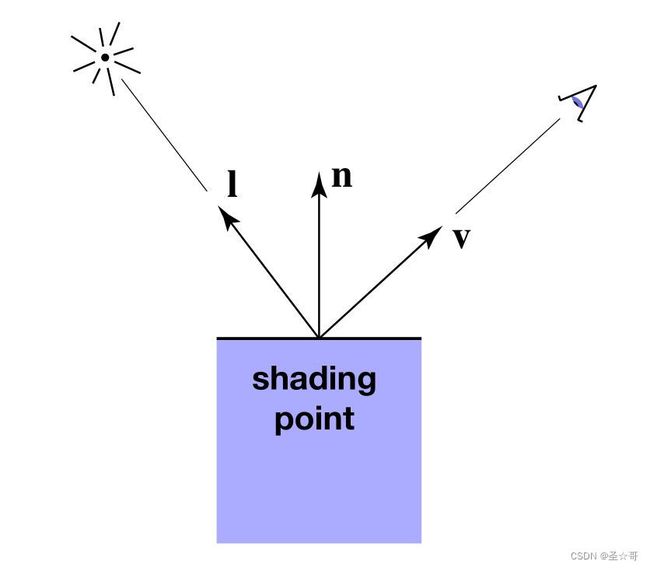
s h a d i n g p o i n t ′ s v a l u e = F ( l , n , v , S u r f a c e p a r a m e t e r s ) shading \ point's \ value = F(\bold{l},\bold{n},\bold{v}, Surface\ parameters) shading point′s value=F(l,n,v,Surface parameters)
其中
l : = L i g h t D i r e c t i o n \bold{l}:=Light \ Direction l:=Light Direction,着色点到某一光源的方向,可以有多个光源;
n : = S u r f a c e N o r m a l \bold{n}:=Surface \ Normal n:=Surface Normal,着色点平面的法线;
v : = V i e w e r D i r e c t i o n \bold{v}:=Viewer \ Direction v:=Viewer Direction,着色点到相机的方向。
S u r f a c e p a r a m e t e r s : = Surface\ parameters:= Surface parameters:=表面参数,比如color(物体固有颜色)、shininess(光滑度)等等。
Blinn-Phong Reflection Model

这是一个经验公式,式中每一项的含义如下:
Ambient Term
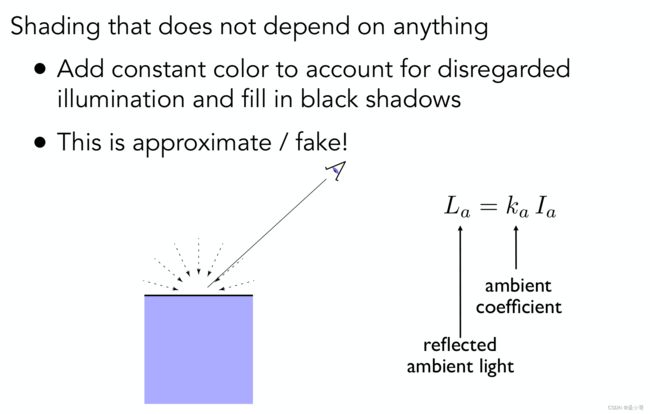
Diffuse Term
Lambert定律 + 能量守恒 + 独立于观测方向
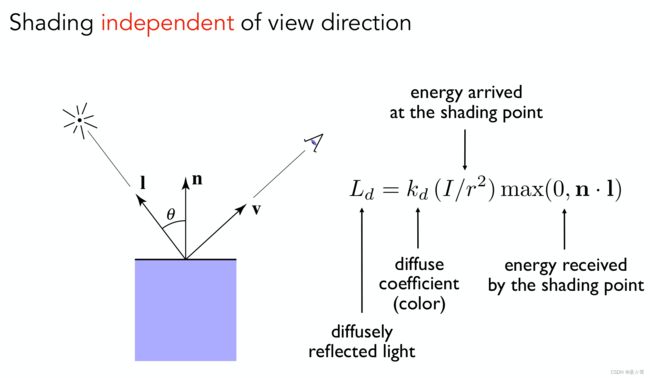

Speculator Term
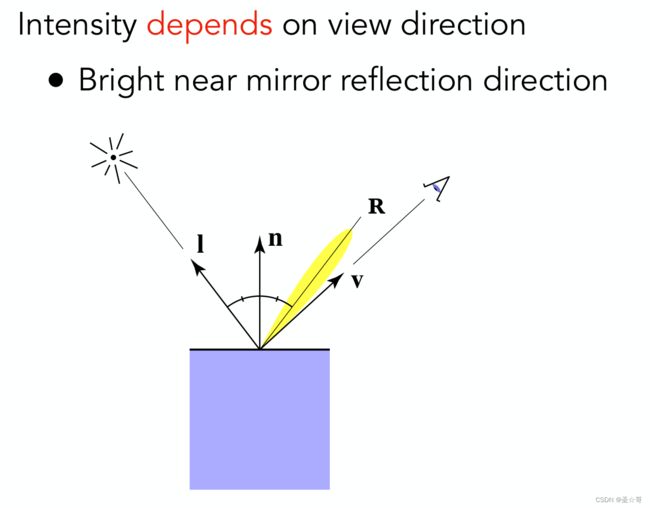


Shading Frequencies
1. Flat shading - Shade each triangle

2. Gouraud shading - Shade each vertex

一般情况下,一个顶点的法向量可以通过共享它的各个三角面的法向量取平均获得。
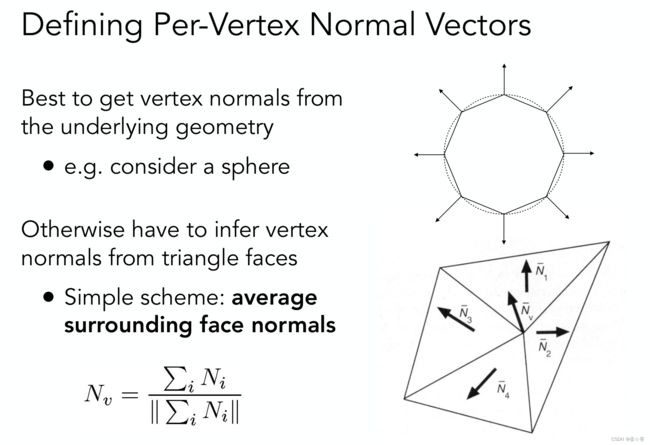
3. Phong shading - Shade each pixel

通常来说一个三角形覆盖了多个像素(至于一个像素被多个三角形覆盖的情况,我不太清楚怎么办,有大佬知道的话可以在评论区指点一下),三角形内一个像素点的属性值可以通过三角形顶点进行线性插值获得,这里就可以用到重心坐标插值法,虎书第二章有公式推导,这里不再赘述。

重心坐标
三种表示方法:
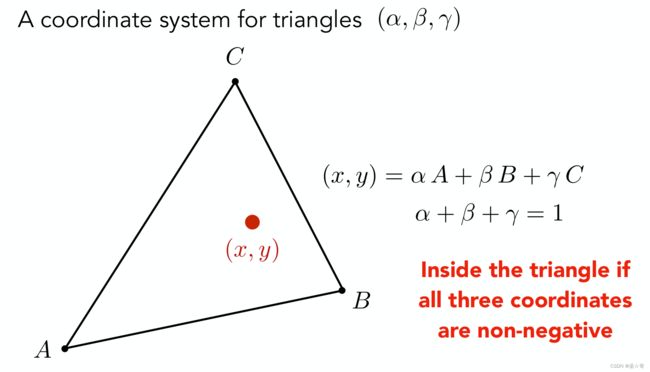
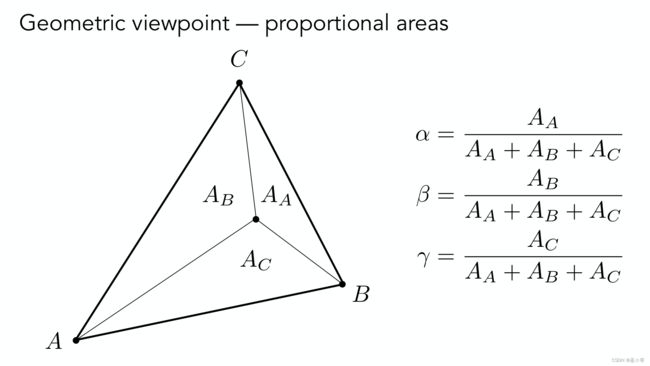
以下写法在实际应用中常见:

需要强调的是:
-
重心坐标插值的对象可以是颜色,也可以是纹理、深度、法线向量、材质属性等其他类型的值;
-
某一点的重心坐标在投影前后通常来说是不一样的。
三种shading model的比较与选择
在模型几何比较简单时(指顶点、面数少),shading效果差异比较大,但在顶点数很多时(如今大多模型如此),三者差距不大,这时候可以使用计算开销更低的Flat shading。

Graphics Pipeline(Real-time Rendering)

这里介绍了渲染管线的流程,以及每一个阶段干的事情。
1. Vertex Processing AND Triangle Processing
MVP变换,将3D空间中的顶点位置信息投射到屏幕坐标系,顶点的连接关系、属性等信息不会因为该变换而改变。因此,MVP变换前后的三角形是由同样的三个顶点确定的三角形。

2. Rasterization
光栅化,相关内容见Lecture05-06 Rasterization。
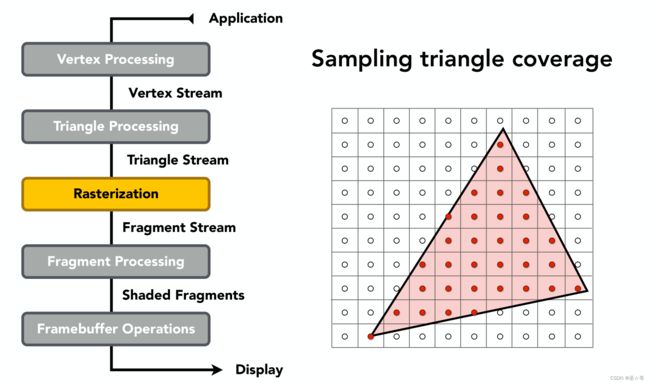
3. Fragment Processing
Fragment即片段,这里理解为像素,深度可见性测试也可以归为光栅化的一部分。

4. Framebuffer Operations
帧缓存操作,尚未细讲。
Shading涉及的流程
Shading所涉及的流程取决于Shading模型的选取:对于Gouraud shading,其对各个顶点着色,因而涉及Vertex Processing;对于Phong shading,其对各个像素着色,因而涉及Fragment Processing。
Texture Mapping也涉及这两个流程。

现代GPU中已经封装了这套渲染管线,其中Vertex Processing和Fragment Processing是可编程的,它们共同构成了Shader。
Shader程序与一般程序的主要区别:Shader函数是逐像素执行的,即函数描述的是对一个像素的操作。


Texture
Texture Mapping
Shader程序描述了对每一个像素所作的同样操作,但不能使得不同像素的颜色不一样,因而需要纹理贴图(Texture)。
注意到三维世界中的各表面都是2D的(尽管表面的形状各异),因而3D物体表面上的每一个点都可以唯一映射到纹理贴图上的某一点。

纹理映射指的是将物体空间中的每个三角形顶点映射至纹理空间上的对应坐标位置。
纹理贴图的生成方法:
-
艺术家(美工)绘制(繁重,但目前仍是主流),比如平铺(Tiled)纹理,要做到无缝衔接,取决于艺术家个人的设计水平以及一些算法(如Wang Tiling);
-
自动化过程(参数化,重大研究方向,尚未到广泛应用阶段)。
Applying Textures
下图描述了流程:
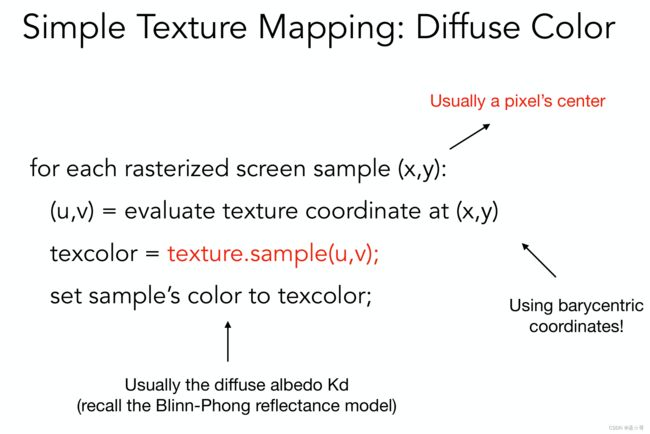
循环第二行是查询坐标 ( u , v ) (u,v) (u,v)对应的纹理颜色。
Problems in Simple Texture Mapping
1. 纹理过小 - Texture Magnification(纹理放大)
纹理图分辨率过小而被拉大,从而查询的多个邻近点(位置描述为浮点数,四舍五入至整数)的像素对应同一个纹理元素(texel),看起来非常奇怪。

解决方案有双线性插值(Bilinear Interpolation)和双三次插值(Bicubic Interpolation),后者计算量更大,但效果更好。
对某个纹素,找其邻近的四个纹素进行插值,所谓双线性插值,即先按照 u u u方向插值出两点的属性值,之后以这两点按照 v v v方向再插值出目标点最终的值。
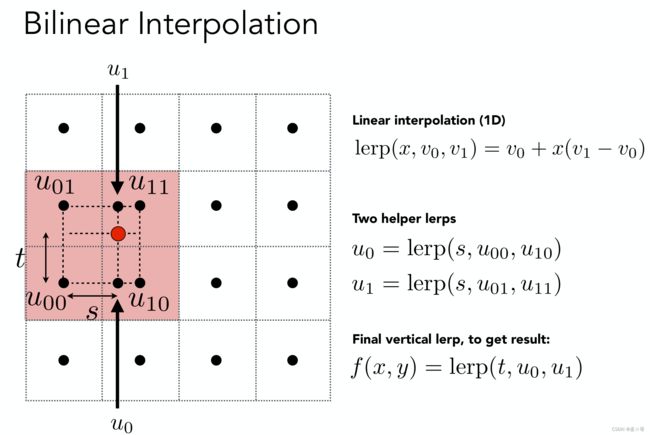
2. 纹理过大 - Texture Minification(纹理缩小)
这个情况处理比较麻烦,其带来的问题如下图所示,可见近处的出现了走样现象,而远处出现了摩尔纹。
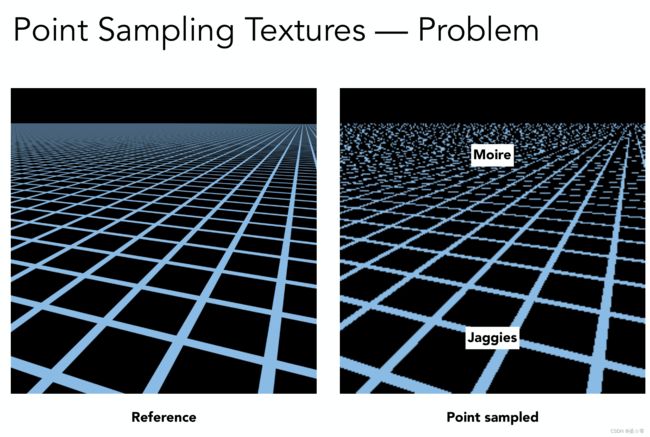
其原因是场景远处的一个像素可能对应多个纹素,而只选取了某一个纹素值作为该像素的值,实际应当查询该像素对应纹素区域的平均值。

一种解决方法提高采样率,但这也会增加计算开销。
另一种方法,不改变采样率的前提下,只需要快速进行区间查询即可。
Solution:Mipmap - fast, approximate, square Range Queries
类似图像金字塔,存储开销不超过原图的 4 3 \frac{4}{3} 34。

根据屏幕像素查询纹理空间中对应覆盖的方形区域,通过以下近似公式计算方形区域边长,从而得知覆盖区域大小,进而可以到相应层查找平均值。

应用Mipmap后的效果如下左图,可见在边界处过渡不平滑,原因是Mipmap层级是整形离散的,因此可以在层与层之间进行插值——三线性插值,其效果如下右图所示。


所谓三线性插值,在每一层的双线性插值基础上,相邻层之间再进行一次插值。

Mipmap局限
可以观察一下简单纹理映射、超采样以及Mipmap处理的结果(从左至右),可见Mipmap在远处的细节过于模糊(Overblur)。



其原因是Mipmap只能查询正方形区域。
一种解决方案是各向异性过滤(Anisotropic Filtering),它可以查询矩形区域,其存储开销近似为原始的4倍,但仍然不能解决不规则覆盖,比如上图中倾斜比较厉害的矩形区域。
所谓各向异性,这里指水平和竖值方向不完全一致,即对应矩形。
要解决倾斜等不规则覆盖的情况,可以采用EWA过滤,但其计算开销更大,具体算法自行搜索研究。

Applications of textures
纹理的概念:现代GPU中,纹理即一块内存以及对该内存的区间查询。
1. 环境贴图/光照 Environment Map/Lighting
用纹理来描述环境光。

球状环境贴图:
这种描述下,顶部和底部出现了扭曲的问题,可以参考地球仪——高纬度下的陆地被拉伸了,即比实际面积更大。
一种解决方法,即将纹理映射到包围球面的立方体上,即立方体贴图。
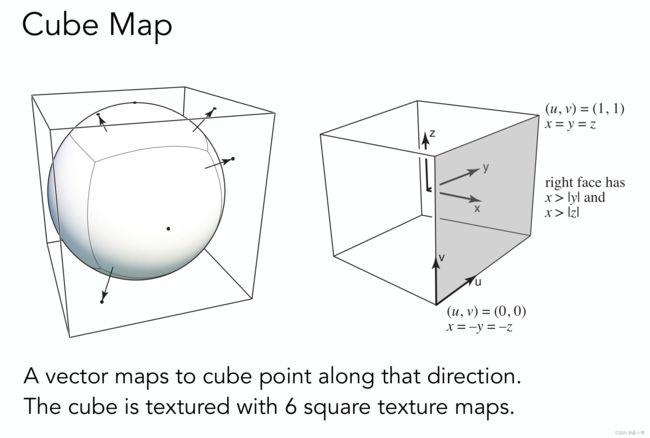
展开后如下:
2. 不表示颜色的贴图 —— 高度/法线贴图
不改变几何形体的情况下,用纹理定义高度,从而形成凹凸感,欺骗人的眼睛。


求法线的方法:先表示切线,然后逆时针旋转90度即可。


更先进的方法——位移贴图,它实际移动了顶点位置。
它的优势:① 边缘处更真实(下图中法线贴图边缘是平的,但实际应该凹凸不平);② 阴影更真实。
它的限制:要求三角形足够细,即三角形的定点间隔比纹理定义的频率更高。如果三角形比较大,但该处纹理频率较高,一种解决方法是拆分大三角形至许多小三角形(如DirectX的dynamic tessellation)。

3. 纹理的其他应用
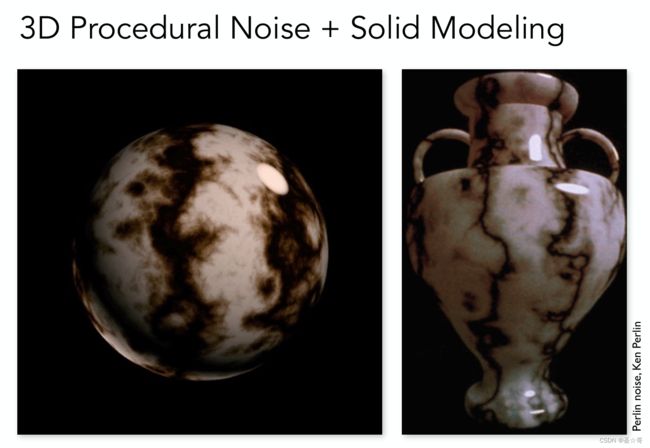
3D程序纹理
定义三维空间噪声函数(如Perlin Noise),不需要生成贴图。
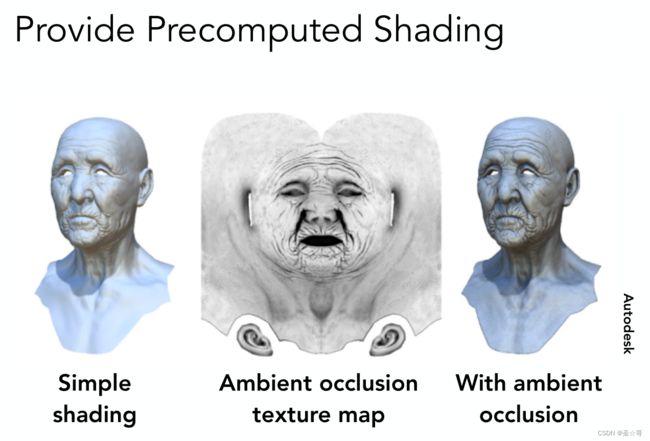
预先计算 - 环境光遮蔽
预处理阴影,即把阴影信息提前写入纹理贴图中(环境光遮蔽纹理,每个纹素的值为0-1),应用时用它乘以计算的着色结果即可。这样可以节省很多计算时间。
环境光遮蔽也可以实时计算。
体渲染
将信息存储在三维空间中,即“3D纹理”。

可见,纹理的概念非常广泛,其存储的信息非常多样。
笔者水平有限,若总结存有不妥之处,恳请各位大佬们批评指正~