16-数据结构-图的存储结构

简介：主要为图的顺序存储和链式存储。其中顺序存储即邻接矩阵的画法以及代码，邻接矩阵又分为有权图和无权图，区别就是有数据的地方填权值，无数据的地方可以填0或者∞，而有权图和无权图，又细分为有向图和无向图。无向图为对称矩阵，因为没有方向可言，出度入读一样。而有向图则有区分，对了，邻接矩阵横着看，是出度，竖着看是入读。链式存储中则包含邻接表、十字链表和邻接多重表，其中邻接表，有向图和无向图都可以，而十字链表是其邻接表有向图的优化，可以同时计算入读和出度，而邻接多重表，是邻接表无向图的优化，可以节约一半的边数空间，由原来的顶点数+2*总边数，变为了顶点数+总边数。

目录

一、顺序存储-邻接矩阵

1.1-简介

1.2-代码

1.3-运行结果

二、链式存储-邻接表

2.1邻接表

2.1.1.代码

2.2十字链表

2.2.1代码

2.3邻接多重表

2.3.1代码：

---

一、顺序存储-邻接矩阵

1.1-简介

图嘛，自然是包括了顶点和边。而邻接矩阵则是通过数组的形式，表示图。

其中需要一个一维数组，用来存储顶点的信息——顶点即一个单位像学生1，学生2之类的。

还需要一个二维数组，就是邻接矩阵，来存储顶点之间的关系；其次，则是记录，图中顶点数和边的总数。

我代码的思路，是自己想的，从创建到可以运行，如果遇到简单的，我后期再来改。

思路：

1. 先初始化图，给图输入想要的顶点数和边数。其次初始化一维数组和二维数组。
2. 创建以及输入数据，先给顶点的信息，输入顶点数组中。随后是进行判断，看是有向图还是无向图。（这里面默认是无权图）（有权图，只不过又多了一组需要手动输入的数字）。
3. 无向图，是对称矩阵，输入想要的边的关系，即1与2，则邻接矩阵对应的直接改为1，表示两个点之间相连，同时更新对称位置也为1.
4. 有向图。则是更新一个就行，另一个不更新。

1.2-代码

#include 
#define Max 10
#include 
//图的顺序存储_邻接矩阵
typedef struct
{
	char vertex[Max];    //存放顶点的一维数组 
	int  edge[Max][Max];	//表示顶点之间关系的二维数组； 
	
	int vertex_num;  //顶点数 
	int edge_num;    //边数 
	
}MGragh; 
//初始化邻接矩阵 
void InitMGragh(MGragh *a) 
{
	printf("添加几个顶点\n");
	int x;
	scanf("%d",&x); 
	//赋值	
	a->vertex_num=x;
	
	printf("有多少条边\n"); 
	int c; 
	scanf("%d",&c);
	//赋值 
	a->edge_num=c;
	//初始化邻接矩阵存储边信息的二维数组 
	a->edge[Max][Max];
	int p,q;
	for(p=0;pvertex_num;p++)
	{
		for(q=0;qvertex_num;q++)
		{
			a->edge[p][q]=0;
		}
	} 
	//初始化，顶点数组 
	a->vertex[a->vertex_num]='0'; 	
}
//打印邻接矩阵 
void PrintMGragh(MGragh *a)
{
	int p,q;
		for(p=0;pvertex_num;p++)
		{
			for(q=0;qvertex_num;q++)
			{
				
				printf("%d ",a->edge[p][q]);
			}
			printf("\n");
		} 
}
void Creat_MGragh(MGragh *a)
{
	printf("图的顶点数%d\n",a->vertex_num);
	int i=0;
	printf("请加顶点到顶点数组\n"); 
	for(i=0;ivertex_num;i++)
	{	printf("i=%d\n",i);
		char x;
		x=getchar();
		char k;//由于单个字符输入，回车也在输入序列中，因此还需要一个变量，来吃掉回车 
		k=getchar();
		a->vertex[i]=x;
	}
	printf("您想弄成无向图还是有向图,1为无向图，2为有向图\n");
	int text;
	scanf("%d",&text);
	if(text == 1)
	{
		printf("请添加顶点间关系\n"); 
		
		int w=0;
		while(w!=2)
		{
			printf("哪个顶点和哪个顶点之间有联系\n");
			int d1,d2;
			scanf("%d %d",&d1,&d2);
			a->edge[d1-1][d2-1]=1;
			a->edge[d2-1][d1-1]=1;
			printf("是否还需要继续添加，是填1，否填2\n");
			scanf("%d",&w); 
		}		
	}
	else
	{
		printf("请添加顶点间关系\n"); 
		
		int w=0;
		while(w!=2)
		{
			int d1,d2;
			printf("从哪个顶点到哪个顶点\n");
			scanf("%d %d",&d1,&d2);
			a->edge[d1-1][d2-1]=1;
			printf("是否还需要继续添加，是填1，否填2\n");
			scanf("%d",&w); 
		}
	} 
}

int main()
{
	MGragh a;
	//初始化图 
	InitMGragh(&a);
	//创建邻接矩阵图 
	Creat_MGragh(&a); 
	//打印邻接矩阵 
	PrintMGragh(&a);
	return 0;
 } 

1.3-运行结果

二、链式存储-邻接表

2.1邻接表

        简介：邻接表，实际上主要为一个顶点表后面串着相应的边表。在记录总的边数和顶点数。

为链式存储。它适用于稀疏图，方便计算出度，只需要找到相应的顶点，然后通过该顶点的单链表，往后遍历串就行。但入读则需要遍历每个顶点单链表。

无向图，有向图都可以。有向图，每个顶点传一个方向的，要么都弄出度，要么都能入读。所以它所需要的空间为O(顶点数+总边数)；而无向图，则是与该顶点相连的，都穿起来，因此所需要的存储空间为O(顶点数+2*总边数)

2.1.1.代码

        边表ArcNode：包括该点下标和下一个指针域。

//边表 
typedef struct ArcNode
{
	int NodeName;
	struct ArcNode *next;
	
}ArcNode; 

         顶点表：存储图的各个顶点，每个顶点后面实际上是对应的从他出发的出度的单链表。

//顶点表
typedef struct
{
	int data;//顶点内容 
	ArcNode* first;	//顶点标的链的头指针 
	
}VNode;

        邻接表：最后才是邻接表，即只需要通过顶点表，就可访问其各个顶点的出度。

//创建邻接表，包含顶点表和边表，以及边数和顶点数的记录 
typedef struct
{
	VNode vertice[vertice_num];//顶点表，每个顶点标中的数据，串成一个对应的链 
	int vexnum;//顶点数 
	int edgenum;//边数	
}ALGragh; 

       由于实现的话，以我目前的水平，感觉有点麻烦，需要遍历每个顶点，每个顶点还需要创建边表结点，还需要给每个顶点单链表，形成，目前没思路，写到中间卡壳了，以后熟练了，再来补实现        

2.2十字链表

        简介：十字链表仅适用于有向图，为了弥补邻接表中有向图只能计算单向的度。

多了一些入读的信息。先给邻接表的形式，出度画出来。随后再找顶点表中各个顶点的入读，入0的入读，从0出发，看边表中，哪个终点为0，则连起来，没有则置为空。

        十字链表仍然是通过顶点表，即可遍历相应顶点的出度链和入读链，即可直到相应顶点的出度和入读。

2.2.1代码

//边表
typedef struct ArcNode
{
	int tailvex,headvex;//弧尾tail弧头head     弧尾（起点）->弧头（终点） 
	struct ArcNode *hlink,*tlink;//指针域，即出度指针域为弧头，入读指针域为弧尾，先连接弧头指针域，出度、再连接弧尾指针域 
	char info;//存储信息的指针 
}ArcNode; 
//顶点表
typedef struct VNode
{
	AreNode *firstin,*firstout;//出度入读头指针 
	int data;//顶点信息 
	
}VNode;
//十字链表
typedef struct GLGraph 
{
	VNode xlist[vertice_num];//顶点表 
	int vexnum,edgenum;//顶点数和边数 
	
}GLGraph;  

2.3邻接多重表

简介：邻接多重表仅适用于无向图，是邻接表中无向图，的优化，邻接表中无向图，会重复多连，2*总边数，而邻接多重表节约，为E。

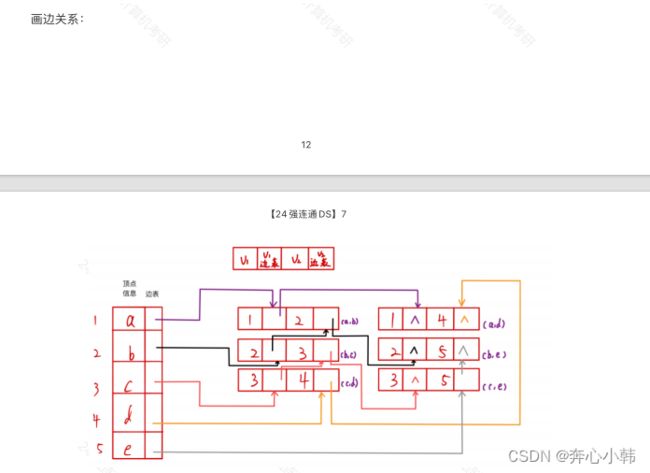
画法：先画出顶点表和边表，边表中为与最左边顶点表中顶点相关的顶点，即边，为边的起点和边的终点，并有两个相关的指针域。第一步，先标记好相应的数值，自上而下画，下方顶点，若有重复的边，则不画。

//强连通机构的例题——不想自己画了，偷个懒

第二步，串链，由左边顶点表中的顶点出发，找右边边表中，与该顶点相同的指针域，连接上即可，如b的下标是2，从b出发，找右边边表中2的指针域。2的指针域第一行有一个，第二行有两个，给这三个串上即可。

2.3.1代码：

//邻接多重表-无向图
//边表
typedef struct AreNode
{
		int mark; //标记是否串过
		int ivex,jvex;//表示弧的两个顶点
		struct AreNode *ilink,*jlink;
		char info;//其他信息	
}AreNode;
//顶点表
typedef struct VNode
{
	int data;//顶点信息 
	AreNode *first;//指向边表中第一个挨着该顶点的结点 
	
}VNode;
//邻接多重表
typedef struct  AMLGraph
{
	VNode xlist[vertice_num];//顶点表 
	int vexnum,edgenum;//总边数和总结点数 
}AMLGraph;