基于夹角余弦计算轨迹相似度
目录
- 背景
- 预备知识
- 算法流程图
- 核心代码
- 优缺点
背景
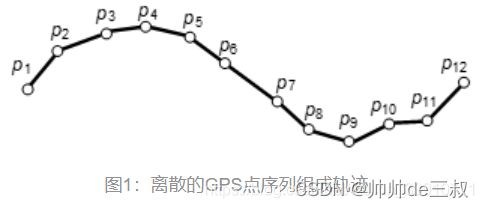
同一个司机同一辆车跑同一个运单,结果来自中交兴路定位和来自手机app的定位画出的两条轨迹形同陌路,有时候你会觉得就是一车辆在不同时间的位置,几乎在一条曲线上,如图1所示,有时候你又会觉得根本就是两辆车的轨迹,如图2所示,来自中交兴路和手机app的两者轨迹是否存在亲近关系呢?如果存在,亲近关系又是多少?该如何科学合理度量?
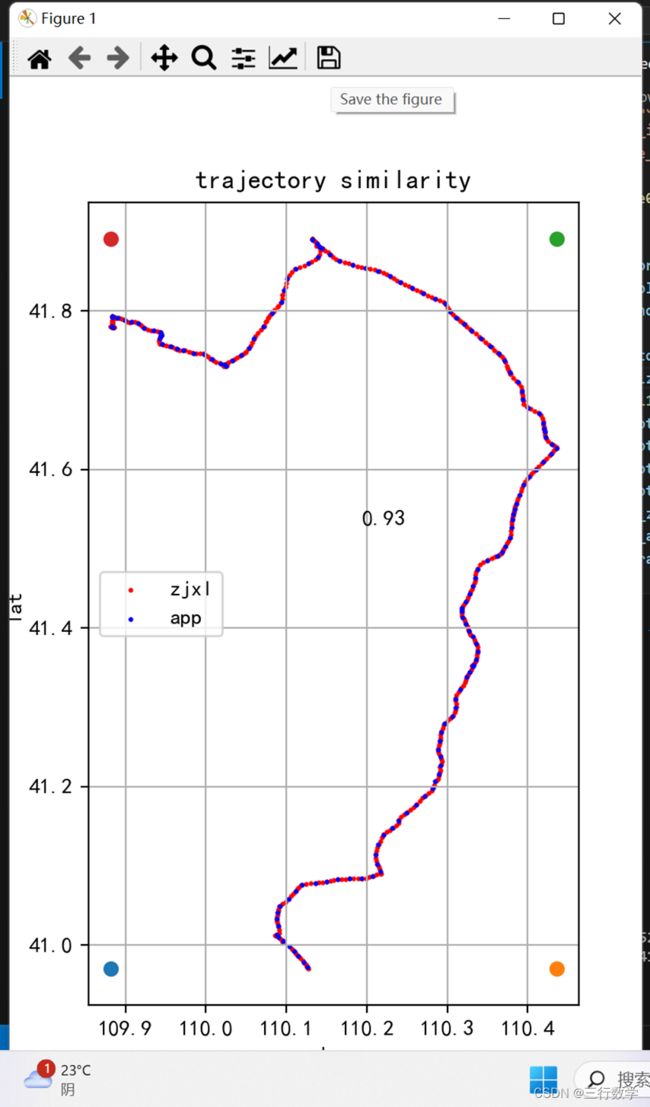 图1 轨迹1 图1 轨迹1
|
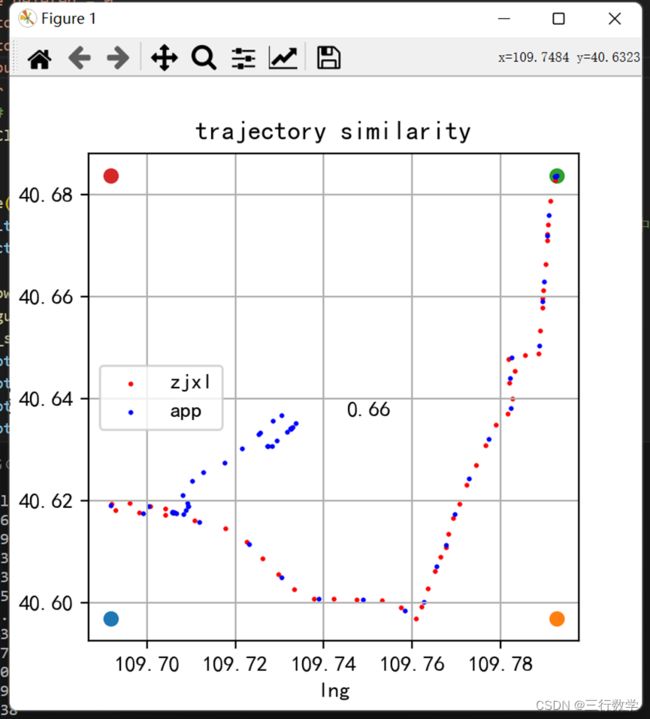 图2 轨迹2 图2 轨迹2
|
预备知识
- 轨迹
物理学把物体运动所形成的几何对象做成的集合称为轨迹,用以刻画物体运动的时空变化,轨迹具有时空特性,是一种时空数据,在物联网如何如此发达的今天,我们人类各种各样的的设备无时无刻不在生成轨迹,如微信轨迹,跑步app记录轨迹,车载GPS设备记录,Carplay,Carlife等手机导航软件轨迹等,轨迹通常可以表示为有一些经纬度构成的时间序列
| updatetime | lng | lat |
|---|---|---|
| 2023-07-22 00:08:16 | 109.77707386212175 | 40.64164611778668 |
| 2023-07-22 00:08:26 | 109.77707386212175 | 40.64164611778668 |
| 2023-07-22 00:20:56 | 109.7769681408526 | 40.64316816811425 |
| 2023-07-22 00:35:56 | 109.7769681408526 | 40.64316816811425 |
| … | … | … |
| 2023-07-22 01:10:16 | 109.776924186014 | 40.64319521851351 |
其中,updatetime表示轨迹点记录的时间,是有先后顺序,lng表示该设备在对应时刻所在的经度,lat表示该设备在对应时刻的纬度,任何一条轨迹可以用如下数学表达式表示
L = [ p 1 , p 2 , ⋯ , p n ] L = [p_1,p_2, \cdots, p_n] L=[p1,p2,⋯,pn]
其中, p i ( 1 ≤ i ≤ n ) p_i(1\leq i\leq n) pi(1≤i≤n)表示第i个轨迹点的位置信息 p i = [ l n g i , l a t i ] p_i=[lng_i, lat_i] pi=[lngi,lati],这样,一条轨迹可以描述成由一些经纬度构成的轨迹点构成的时序集合,再考虑不同设备采集频率,信号传递等因素,所以在轨迹相似度计算的时候应该尽量使用与轨迹点直接关系的测度,如轨迹点的数目等,而不应该使用有轨迹点组合而成的几何对象,如线,面,多边形等。
现在,为了刻画两条轨迹的相似度,我们需要为任意两个轨迹定义出一个相似函数,可以依循从一般到特殊再到一般的思路进行,先来看一下相似函数应该具备哪些性质
- 相似函数性质
数学上往往喜欢用距离等公式来刻画两个对象的相似性,根据距离性质我们可以约定相似函数应该具备对称性,具体的,对任意两条轨迹 L i , L j L_i, L_j Li,Lj,如果有
S i m ( L j , L i ) = S i m ( L i , L j ) Sim(L_j, L_i) = Sim(L_i, L_j) Sim(Lj,Li)=Sim(Li,Lj)
则称相似函数Sim满足对称性。
- 两个向量的相似度
数学上常用夹角余弦函数来刻画2个向量的相似度,假设 α = ( x 1 , y 1 ) \alpha =(x_1, y_1) α=(x1,y1), β = ( x 2 , y 2 ) \beta =(x_2, y_2) β=(x2,y2) 是平面上的两个向量,现在定义 α , β \alpha, \beta α,β的相似度如下
C o s S i m ( α , β ) = C o s ( α , β ) CosSim(\alpha,\beta) = Cos(\alpha, \beta) CosSim(α,β)=Cos(α,β)
其中, C o s ( α , β ) Cos(\alpha, \beta) Cos(α,β) 表示 α , β \alpha, \beta α,β的余弦相似度,现在用坐标表示
C o s S i m ( α , β ) = ( α , β ) ∣ α ∣ ∣ β ∣ = x 1 x 2 + y 1 y 2 x 1 2 + y 1 2 x 2 2 + y 2 2 CosSim(\alpha, \beta) = \frac{(\alpha, \beta)}{|\alpha||\beta|} = \frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}} CosSim(α,β)=∣α∣∣β∣(α,β)=x12+y12x22+y22x1x2+y1y2
很容易证明夹角余弦具有对称性,取值位于-1到1之间。
- 两个向量组的相似度
在知道如何计算两个向量相似度之后,如何计算两个向量组的相似度呢?我们来考察如下两个向量组
α = ( α 1 , α 2 , ⋯ , α n ) \alpha = (\alpha_1, \alpha_2, \cdots, \alpha_n) α=(α1,α2,⋯,αn)
β = ( β 1 , β 2 , ⋯ , β n ) \beta = (\beta_1, \beta_2, \cdots, \beta_n) β=(β1,β2,⋯,βn)
其中, α i \alpha_i αi表示第i个向量 , β j \beta_j βj表示第j个向量, α , β \alpha, \beta α,β的余弦函数为
C o s S i m ( α , β ) = ( α , β ) ∣ ∣ α ∣ ∣ ∣ ∣ β ∣ ∣ = ∑ i = 1 n α i β i ∑ i = 1 n α i 2 ∑ i = 1 n β i 2 CosSim(\alpha, \beta) = \frac{(\alpha, \beta)}{||\alpha||||\beta||} = \frac{\sum\limits_{i=1}^n \alpha_i\beta_i}{\sqrt{\sum\limits_{i=1}^n \alpha_i^2}\sqrt{\sum\limits_{i=1}^n \beta_i^2}} CosSim(α,β)=∣∣α∣∣∣∣β∣∣(α,β)=i=1∑nαi2i=1∑nβi2i=1∑nαiβi
- 两条轨迹的相似度函数构造
在知道相似函数的性质以及向量组的相似度刻画后,现在,我们可以来定义两条由同样数目的轨迹点构成的轨迹的相似函数,设另一条轨迹
Q = [ q 1 , q 2 , ⋯ , q n ] Q = [q_1,q_2, \cdots, q_n] Q=[q1,q2,⋯,qn]
其中, q i = ( l n g i ′ , l a t i ′ ) ( 1 ≤ i ≤ n ) q_i=(lng_i', lat_i')(1\leq i\leq n) qi=(lngi′,lati′)(1≤i≤n)表示第i个轨迹点的位置信息。现在,来计算轨迹 L , Q L, Q L,Q的相似度,为此,先对 L , Q L, Q L,Q的向量化
L = [ p 1 , p 2 , ⋯ , p n ] = [ p 1 p 2 → , ⋯ , p n − 1 p n → ] = [ ( l n g 2 − l n g 1 , l a t 2 − l a t 1 ) , ⋯ , ( l n g n − l n g n − 1 , l a t n − l a t n − 1 ) ] = [ ( Δ l n g 1 , Δ l a t 1 ) , … , ( Δ l n g n − 1 , Δ l a t n − 1 ) ] \begin{aligned} L =& [p_1,p_2, \cdots, p_n] \\ =& [\overrightarrow {p_1p_2},\cdots, \overrightarrow {p_{n-1}p_n}]\\ =& [(lng_2-lng_1, lat_2-lat_1), \cdots, (lng_n-lng_{n-1}, lat_n- lat_{n-1})]\\ =& [(\Delta lng_1,\Delta lat_1), \dots, (\Delta lng_{n-1}, \Delta lat_{n-1})] \end{aligned} L====[p1,p2,⋯,pn][p1p2,⋯,pn−1pn][(lng2−lng1,lat2−lat1),⋯,(lngn−lngn−1,latn−latn−1)][(Δlng1,Δlat1),…,(Δlngn−1,Δlatn−1)]
Q = [ q 1 , q 2 , ⋯ , q n ] = [ q 1 q 2 → , ⋯ , q n − 1 q n → ] = [ ( l n g 2 ′ − l n g 1 ′ , l a t 2 ′ − l a t 1 ′ ) , ⋯ , ( l n g n ′ − l n g n − 1 ′ , l a t n ′ − l a t n − 1 ′ ) ] = [ ( Δ l n g 1 ′ , Δ l a t 1 ′ ) , … , ( Δ l n g n − 1 ′ , Δ l a t n − 1 ′ ) ] \begin{aligned} Q =& [q_1,q_2, \cdots, q_n] \\ =& [\overrightarrow {q_1q_2},\cdots, \overrightarrow {q_{n-1}q_n}]\\ =& [(lng_2'-lng_1', lat_2'-lat_1'), \cdots, (lng_n'-lng_{n-1}', lat_n'- lat_{n-1}')]\\ =& [(\Delta lng_1',\Delta lat_1'), \dots, (\Delta lng_{n-1}', \Delta lat_{n-1}')]\\ \end{aligned} Q====[q1,q2,⋯,qn][q1q2,⋯,qn−1qn][(lng2′−lng1′,lat2′−lat1′),⋯,(lngn′−lngn−1′,latn′−latn−1′)][(Δlng1′,Δlat1′),…,(Δlngn−1′,Δlatn−1′)]
接着,计算 L , Q L, Q L,Q的余弦相似度
C o s S i m ( L , Q ) = ( L , Q ) ∥ L ∥ ∥ Q ∥ = ( ( Δ l n g 1 , Δ l a t 1 ) , … , ( Δ l n g n − 1 , Δ l a t n − 1 ) ) , ( ( Δ l n g 1 ′ , Δ l a t 1 ′ ) , … , ( Δ l n g n − 1 ′ , Δ l a t n − 1 ′ ) ) ∥ ( ( Δ l n g 1 , Δ l a t 1 ) , … , ( Δ l n g n − 1 , Δ l a t n − 1 ) ) ∥ ⋅ ∥ ( ( Δ l n g 1 ′ , Δ l a t 1 ′ ) , … , ( Δ l n g n − 1 ′ , Δ l a t n − 1 ′ ) ) ∥ = ∑ i = 1 n Δ l n g i Δ l n g i ′ + ∑ i = 1 n Δ l a t i Δ l a t i ′ ∑ i = 1 n ( Δ l n g i 2 + Δ l a t i 2 ) ∑ i = 1 n ( Δ l n g i ′ 2 + Δ l a t i ′ 2 ) \begin{aligned} CosSim(L, Q) &= \frac{(L, Q)}{\lVert L\rVert \lVert Q\rVert} \\ &= \frac{((\Delta lng_1,\Delta lat_1), \dots, (\Delta lng_{n-1}, \Delta lat_{n-1})),((\Delta lng_1',\Delta lat_1'), \dots, (\Delta lng_{n-1}', \Delta lat_{n-1}'))}{\lVert((\Delta lng_1,\Delta lat_1), \dots, (\Delta lng_{n-1}, \Delta lat_{n-1}))\rVert·\lVert((\Delta lng_1',\Delta lat_1'), \dots, (\Delta lng_{n-1}', \Delta lat_{n-1}'))\rVert}\\ &= \frac{\sum\limits_{i=1}^n \Delta lng_i\Delta lng_i' + \sum\limits_{i=1}^n \Delta lat_i\Delta lat_i'} {\sqrt{\sum\limits_{i=1}^n ( \Delta lng_i^2+\Delta lat_i^2)}\sqrt{\sum\limits_{i=1}^n (\Delta lng_i'^2+\Delta lat_i'^2)}} \end{aligned} CosSim(L,Q)=∥L∥∥Q∥(L,Q)=∥((Δlng1,Δlat1),…,(Δlngn−1,Δlatn−1))∥⋅∥((Δlng1′,Δlat1′),…,(Δlngn−1′,Δlatn−1′))∥((Δlng1,Δlat1),…,(Δlngn−1,Δlatn−1)),((Δlng1′,Δlat1′),…,(Δlngn−1′,Δlatn−1′))=i=1∑n(Δlngi2+Δlati2)i=1∑n(Δlngi′2+Δlati′2)i=1∑nΔlngiΔlngi′+i=1∑nΔlatiΔlati′
算法流程图
1,传入中交兴路轨迹和手机app轨迹两条轨迹数据;
2,分别对两者轨迹数据按照经纬度去重;
3,初步比较两者轨迹,包括长度,完整度;
5,比较两个轨迹点的长度大小,取较小的那个长度作为较长的那条轨迹聚类参数k;
6,对较长的那条轨迹按参数k进行kmeans聚类成新的轨迹, 使得聚类后的新轨迹与原来那条较短的轨迹具有相同的轨迹点数,从而达到数据对齐,因为夹角余弦计算需要用到向量内积,必须对齐;
7,计算较短的那条轨迹和较长的那条聚类后的轨迹两者的夹角余弦;
核心代码
# -*- encoding: utf-8 -*-
'''
@Project : trajectorySimilarity
@Desc : 轨迹相似度计算
@Time : 2023/08/23 13:55:37
@Author : 帅帅de三叔,[email protected]
'''
def trajectoryCluster(trajectory, k): # 使用KMeans, DBSCAN聚类算法进行路段划分
####先kmeans首次聚类,为每一个轨迹点分配一个类
locations = np.array(trajectory[['lat','lng']]) #位置数据
kmeans = KMeans(n_clusters = k)
kmeans.fit(locations)
labels = kmeans.labels_ #
score = silhouette_score(locations, labels, metric='euclidean') #轮廓系数
# print("一共聚了{}类, 轮廓系数为{}".format(labels.max() - labels.min(), score))
cluster_label = pd.DataFrame({"cluster_label": labels})
trajectory.reset_index(drop=True, inplace=True)
cluster_label.reset_index(drop=True, inplace=True)
cluster_data = pd.concat([trajectory, cluster_label], axis = 1, ignore_index=True) #带标签的行驶记录
cluster_data.columns= ['lng', 'lat', 'cluster_label']
cluster_data['cluster_label'] = [str(i) for i in cluster_data['cluster_label']]
#####对每一个聚合出来的类,找出类代表,从而减少轨迹数量
rep_trajectory = pd.pivot_table(cluster_data, index =['cluster_label'], values={'lng':'np.mean', 'lat':'np.mean'})
rep_trajectory = rep_trajectory[['lng', 'lat']]
# print("轨迹点代表\n", rep_trajectory)
return rep_trajectory
def calDistance(point1, point2): #计算两点之间的曼哈顿距离
manhattan_distance = np.abs(point1[0] - point2[0]) + np.abs(point1[1]-point2[1])
return manhattan_distance
def trajectorySort(trajectory, init_point): #对无序的轨迹点进行排序得出路径
# print("初始位置", trajectory[0])
num_points = len(trajectory) #总轨迹点数
visited = [False]*num_points
path = [] #用来存放整理后的轨迹点
current_point = init_point #trajectory[0] #当前轨迹点
path.append(current_point) #把当前轨迹点追加近路径
visited[0] = True
while len(path)< num_points:
min_distance = float('inf')
nearest_point = None
for i, point in enumerate(trajectory):
if not visited[i]:
distance = calDistance(current_point, point)
if distance < min_distance:
min_distance = distance
nearest_point = point
if nearest_point is not None:
path.append(nearest_point)
visited[trajectory.index(nearest_point)] = True
current_point = nearest_point
# path.append(path[0]) #形成回路
return path
def cosinValue(traj1, traj2): #两条轨迹的夹角余弦
vector1_lng = [traj1[i+1][0] - traj1[i][0] for i in range(len(traj1)-1)] #轨迹1的经度分量
vector1_lat = [traj1[i+1][1] - traj1[i][1] for i in range(len(traj1)-1)] #轨迹1的纬度分量
vector2_lng = [traj2[i+1][0] - traj2[i][0] for i in range(len(traj2)-1)] #轨迹2的经度分量
vector2_lat = [traj2[i+1][1] - traj2[i][1] for i in range(len(traj2)-1)] #轨迹2的纬度分量
# print(vector1_lng, scale(vector1_lng), StandardScaler().fit_transform(np.array(vector1_lng).reshape(-1, 1)))
# vector1 = [(i, j) for i,j in zip(vector1_lng, vector1_lat)]
# vector2 = [(i, j) for i,j in zip(vector2_lng, vector2_lat)]
a = float(np.dot(vector1_lng, vector2_lng)) + float(np.dot(vector1_lat, vector2_lat)) # 向量点乘
b = np.sqrt(np.dot(vector1_lng, vector1_lng) + np.dot(vector1_lat, vector1_lat)) * np.sqrt(np.dot(vector2_lng, vector2_lng) + np.dot(vector2_lat, vector2_lat))
cosin_value = a/b
return cosin_value
def CosinSimilarity(traj1, traj2):#计算两条轨迹相似度
traj1_len = len(traj1)
traj2_len = len(traj2)
if traj1_len >= traj2_len: #如果轨迹1的长度比轨迹2的长度多,则把轨迹1聚类成轨迹2等长
rep_traj1 = trajectoryCluster(traj1, k = traj2_len)
traj1_points = list(zip(rep_traj1['lng'], rep_traj1['lat']))
path1 = trajectorySort(traj1_points, init_point = (traj1['lng'][0], traj1['lat'][0]))
path2 = list(zip(traj2['lng'], traj2['lat']))
# print("整理后轨迹1\n", path1)
# print("整理后轨迹2\n", path2)
cosin_sim_value = cosinValue(path1, path2)
if traj2_len>traj1_len: #如果轨迹2的长度比轨迹1的长度多,则把轨迹2聚类成轨迹1等长
rep_traj2 = trajectoryCluster(traj2, k = traj1_len)
traj2_points = list(zip(rep_traj2['lng'], rep_traj2['lat']))
path2 = trajectorySort(traj2_points, init_point=(traj2['lng'][0], traj2['lat'][0]))
path1 = list(zip(traj1['lng'], traj1['lat']))
# print("整理后轨迹1\n", len(path1))
# print("整理后轨迹2\n", len(path2))
cosin_sim_value = cosinValue(path1, path2)
print("余弦相似度", cosin_sim_value)
return cosin_sim_value
优缺点
1,利用夹角余弦来刻画轨迹相似度,好构造好计算,直观好理解,可以作为一个baseline;
2,前期数据对齐比较难把握,会丢失部分重要信息;
3,对两者数据量均衡性要求比较高,如果一方远远大于另一方,则容易出现极大极小值,如下图所示;
4,稳定性不够难以复现,这个可以通过轨迹点数目对齐算法来优化;