位运算 |(按位或) &(按位与) ^(按位异或)
目录
文章目录:本章讲解的主要是刷题系列
1:首先会介绍 I & ^这三个操作符的作用,性质
2:三道使用位运算操作符的经典 笔试题(来自剑指offer)
题目链接如下:
1:136. 只出现一次的数字 - 力扣(LeetCode)
2:剑指 Offer 15. 二进制中1的个数 - 力扣(LeetCode)
3:剑指 Offer 56 - I. 数组中数字出现的次数 - 力扣(LeetCode)
文章正式开始~~~
1:位运算符 ^(按位异或) &(按位与) |(按位或)
首先我们得理解位运算符中这个位的含意:这个位其实就是我们平常所说的二进制位,所以位运算符是用来针对二进制位(只含有0和1)进行的运算操作符。
&:这个操作符的名字叫做按位与,不要将他与&&(逻辑或)这个操作符弄混淆了,&的作用是将两个操作数二进制位全为1的才是1,其他的位如果有0或1就会将他变成0.(简单的理解就是:全1才为1,否则这一位的值为0).
比如说:3&5
3&5
假设在32位平台下
3的二进制位:00000000 00000000 00000000 00000011
5的二进制位:00000000 00000000 00000000 00000101
3&5 00000000 00000000 00000000 00000001
全1才为1,其它都为0 |(按位或):这个操作符与上面的操作符有异曲同工之妙,只是它的作用与&相反,二进制位上全0才为0,有1就为1.
3|5的结果如下:
3|5
假设在32位平台下
3的二进制位:00000000 00000000 00000000 00000011
5的二进制位: 00000000 00000000 00000000 00000101
3|5的结果 00000000 00000000 00000000 00000111^按位异或:二进制位相同的为0,相异的为1 ,与此同时^操作符具有交换律与结合律的特点,比如说:a^a=0 因为二进制位全部相同 a^0=a; 0不会改变它原有的位 a^ b^a=b,这里就体现了它的性质,相当于a^a^ b .
知识点已经铺垫完毕,让我们进入习题的讲解吧。
2:经典笔试题(位运算)
题目的难度是由简单到难的哦!
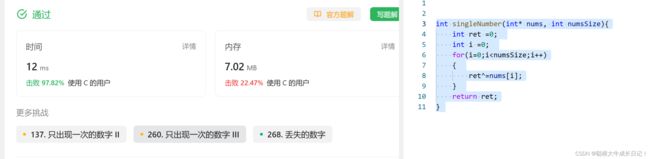
1: 136. 只出现一次的数字 - 力扣(LeetCode)
这道题也可以称作单身狗问题(dog)
首先这个题目的意思就是:给我们一个数组,然后数组中有一个数只出现了1次,其它的数均出现了2次。
这里我们就可以联想到我们上面所讲的^操作符的性质:a^a=0; 0^a=a;
因为数组中有数字出现了2次,那么我们使用^之后就可以消除这两个相同的数了,到最后数组中留下的数字就是那个唯一出现1次的数字
代码:
int singleNumber(int* nums, int numsSize){
int ret =0;
int i =0;
for(i=0;i这道题就很巧妙的使用了^操作符,当然这个题可能还有其它的算法,比如说排序加计数,哈希表...都可以用来实现这个算法。但是我们因为讲的是位操作符,所以就使用了位运算操作符。
2:剑指 Offer 15. 二进制中1的个数
这道题我会用两种解法来讲解这道题:
方法一:移位操作符 加上 &运算符 +计数
思路:假设我们知道一个数因为1的二进制位只有最右边的1位为1其它的位都为0,所以我们将所需要计算数的二进制位的每1位都与1进行&运算
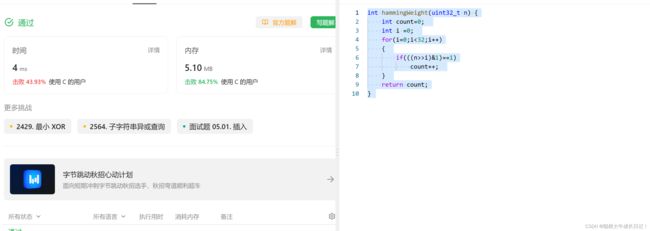
代码:
int hammingWeight(uint32_t n) {
int count=0;
int i =0;
for(i=0;i<32;i++)
{
if(((n>>i)&1)==1)
count++;
}
return count;
} 方法2:将我们所需要求的数的最后一位的1消除,循环进行下去。
方法2:将我们所需要求的数的最后一位的1消除,循环进行下去。
思路:n=n&(n-1);
我们举个列子来讲解:
int hammingWeight(uint32_t n) {
int count=0;
while(n)
{
count++;
n=n&(n-1);
}
return count;
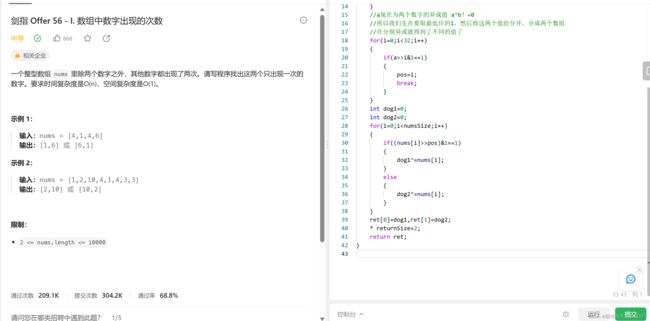
}3:剑指 Offer 56 - I. 数组中数字出现的次数 - 力扣(LeetCode)
这道题相对于前面两道题就有一定的难度了,并没有上面两道题那么直接:
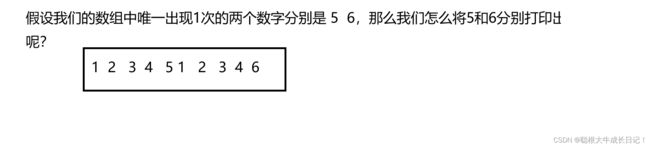
我们通过实际的列子来进行讲解
那么什么又叫分组异或呢?
比如说我们可以把 1 1 3 3 5放在一个数组 把2 2 4 4 6放在另外一个数组,这样我们对每一个数组进行异或就可以得到 5 和6 了。
那么我们如何进行分组呢?
首先我们将数组中的所有数字进行异或得到 5^6,又因为两个数字不可能相等所以异或起来肯定不为1,那么结果中的数二进制位中肯定有一位为1,那么我们就可以利用这个1来进行分组了。
比如5^6
因为5与6在这一位的不同,所以我们将在这一位与5相同的数放进一个组,与5不相同的数我们放到另外的一个数组中,然后分别异或就可以得到答案了。
那么如何找到5与6哪一位不同呢?
首先我们异或整个数组得到5与6的^值,然后将这个值的每一位与1进行&运算,如果找到1位&的结果为1那么我们就可以将这个位置给标记出来,然后再让我们原数组中的每个值移动pos位如果与它&等于1,我们用dog1将它^起来,不等于1那么我们用dog2将它^起来
所以最终我们的dog1为其中的一个值,dog2为其中的第二个值。
代码:
int* singleNumbers(int* nums, int numsSize, int* returnSize){
int*ret=(int*)malloc(sizeof(int)*2);
int i =0;
int pos=0;
int a=0;
for(i=0;i>i&1==1)
{
pos=i;
break;
}
}
int dog1=0;
int dog2=0;
//根据pos位置分为两个数组,直接异或就是我们所需要的答案了
for(i=0;i>pos)&1==1)
{
dog1^=nums[i];
}
else
{
dog2^=nums[i];
}
}
ret[0]=dog1,ret[1]=dog2;
* returnSize=2;
return ret;
}
如果觉得对你有用的话,可以点个赞哦!!