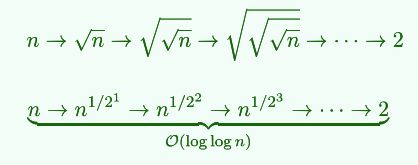数据结构（c++）学习笔记--向量

---

一、抽象数据类型

1、接口与实现

1.1 抽象数据类型=数据模型+定义在该模型上的一组模型

• 抽象定义-外部的逻辑特性-操作&语义

• 一种定义-不考虑时间复杂度-不涉及数据的存储方式

1.2 数据结构=基于某种特定语言，实现ADT的一整套算法

• 具体实现-内部的表现与实现-完整的算法

• 多种实现-与复杂度密切相关-要考虑数据的具体存储机制

1.3 在数据结构的具体实现与实际应用之间，ADT就分工与接口制定了统一的规范

• 实现: 高效实现数据结构的ADT接口操作

• 应用: 便捷地通过操作接口使用数据结构

1.4 按照ADT规范

• 高层算法设计者可与底层数据结构实现者高效地分工协作

• 不同的算法与数据结构可以便捷组合借用

• 每种操作接口只需统一地实现一次，代码篇幅缩短，安全性加强，软件复用度提高

2.从数组到向量

2.1 循秩访问

• 向量是数组的抽象与泛化，由一组元素按线性次序封装而成

  • 各元素与[0, n)内的秩（rank）一一对应

  • 操作、管理维护更加简化、统一与安全

  • 元素类型可灵活选取，便于定制复杂数据结构

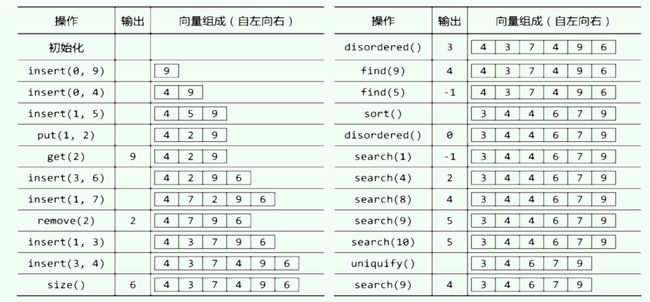
2.2 向量ADT接口

操作	功能	适用对象
size()	报告向量当前的规模（元素总数）	向量
get®	获取秩为r的元素	向量
put(r, e)	用e替换秩为r元素的数值	向量
insert(r, e)	e作为秩为r元素插入，原后继依次后移	向量
remove®	删除秩为r的元素，返回该元素原值	向量
disordered()	判断所有元素是否已按非降序排列	向量
sort()	调整各元素的位置，使之按非降序排列	向量
find(e)	查找目标元素e	向量
search(e)	查找e，返回不大于e且秩最大的元素	有序向量
deduplicate(), uniquify()	剔除重复元素	向量/有序向量
traverse()	遍历向量并统一处理所有元素	向量

2.3 ADT操作实例

#include<iostream> 
#include<vector>

using namespace std; 

int main(){
    vector v; 
    vector s( 43, 47 );
    s.insert( s.begin() + 2, 2022 ); 
    s.erase( s.end() - 40, s.end() ); 
    for ( i = 0; i < s.size(); i++ ) cout << s[i] << endl;
    return 0;
}

3.模板类

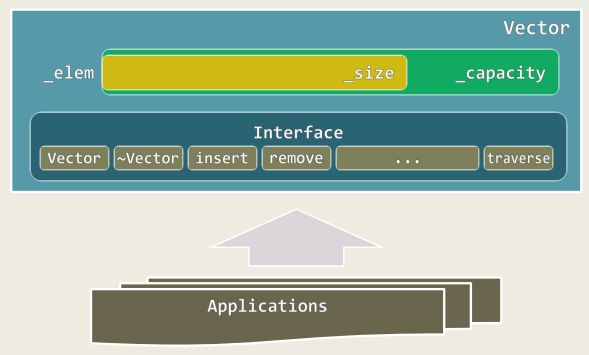
3.1 向量模板类

template<typename T> class Vector {
    private: 
        Rank _size; Rank _capacity; T* _elem; //规模、容量、数据区
    protected: 
        /* ... 内部函数 */构造 + 析构：重载
    public: 
        /* ... 构造函数 */ 
        /* ... 析构函数 */ 
        /* ... 只读接口 */ 
        /* ... 可写接口 */ 
        /* ... 遍历接口 */ 
        /* ... 遍历接口 */
}；

3.2 构造 + 析构：重载

#define DEFAULT_CAPACITY 3 //默认初始容量（实际应用中可设置为更大） 
Vector( int c = DEFAULT_CAPACITY ) 
{ _elem = new T[ _capacity = c ]; _size = 0; } //默认构造 
Vector( T const * A, Rank lo, Rank hi ) //数组区间复制 
{ copyFrom( A, lo, hi ); } 
Vector( Vector const & V, Rank lo, Rank hi ) //向量区间复制 
{ copyFrom( V._elem, lo, hi ); } 
Vector( Vector const & V ) //向量整体复制 
{ copyFrom( V._elem, 0, V._size ); }
~Vector() { delete [] _elem; } //释放内部空间

3.3 基于复制的构造

template<typename T> //T为基本类型，或已重载赋值操作符'=' 
void Vector::copyFrom( T const * A, Rank lo, Rank hi ){  
    _elem = new T[ _capacity = max( DEFAULT_CAPACITY, 2*(hi − lo) ) ];  
    for ( _size = 0; lo < hi; _size++, lo++ ) 
        _elem[ _size ] = A[ lo ];  
} //O(hi – lo) = O(n)

二、可扩充向量

1.算法

1.1 静态空间管理

• 开辟内部数组_elem[]并使用一段地址连续的物理空间

  • _capacity：总容量

  • _size：当前的实际规模n

• 若采用静态空间管理策略，容量_capacity固定，则有明显的不足

  • 上溢/overflow：_elem[]不足以存放所有元素，尽管此时系统往往仍有足够的空间

  • 下溢/underflow：_elem[]中的元素寥寥无几

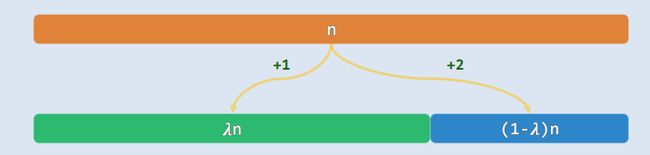
  • 装填因子：λ = _size/_capacity << 50%

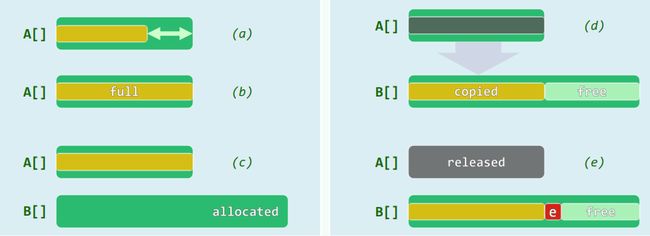
1.2 动态空间管理

• 向量：在即将上溢时，适当扩大内部数组的容量
  

1.3 扩容算法

template void Vector::expand() { //向量空间不足时扩容 
    if ( _size < _capacity ) return; //尚未满员时，不必扩容 
    _capacity = max( _capacity, DEFAULT_CAPACITY ); //不低于最小容量 
    T* oldElem = _elem; _elem = new T[ _capacity <<= 1 ]; //容量加倍 
    for ( Rank i = 0; i < _size; i++ ) //复制原向量内容 
        _elem[i] = oldElem[i]; //T为基本类型，或已重载赋值操作符'=' 
    delete [] oldElem; //释放原空间 
}

2.分摊

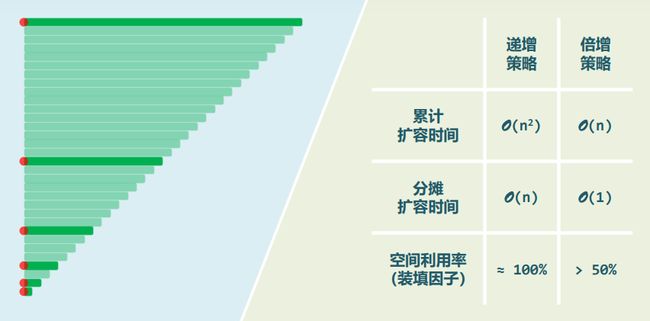
2.1 容量递增策略

• T* oldElem = _elem; _elem = new T[ _capacity += INCREMENT ]; 追加固定增量

• 最坏情况：在初始容量0的空向量中，连续插入n=m·I>>2个元素，而无删除操作
  

• 在不计申请空间操作的情况下，各次扩容过程中复制原向量的时间成本依次为0，I，2I，3I，…，(m-1)I(算术级数)，总体耗时=O($n^2$)，每次操作的分摊成本为O(n)

2.2 容量加倍策略

• T* oldElem = _elem; _elem = new T[ _capacity <<= 1 ]; 容量加倍

• 最坏情况：在初始容量1的满向量中，连续插入n=$2^m$>>2个元素，而无删除操作

• 各次扩容过程中复制原向量的时间成本依次为$1，2，4，8，16，...，2^{m-1},2^m=n$(几何级数)，总体耗时=O(n)，每次操作的分摊成本为O(1)

2.3 对比

2.4 平均分析vs分摊分析

• 平均：根据各种操作出现概率的分布，将对应的成本加权平均

  • 各种可能的操作，作为独立事件分别考查

  • 割裂了操作之间的相关性和连贯性

  • 往往不能准确地评判数据结构和算法的真实性能

• 分摊：连续实施的足够多次操作，所需总体成本摊还至单次操作

  • 从实际可行的角度，对一系列操作做整体的考量

  • 更加忠实地刻画了可能出现的操作序列

  • 更为精准地评判数据结构和算法的真实性能

三、无序向量

1.元素访问

template<typename T> 

//可作为左值：
V[r] = (T) (2*x + 3) T & Vector::operator[]( Rank r ) { 
    return _elem[ r ]; 
}
//仅限于右值
const T & Vector::operator[]( Rank r ) const { 
    return _elem[ r ]; 
}

2.插入

template<typename T> Rank Vector::insert( Rank r, T const & e ) { 
    expand(); //若有必要，扩容 
    for ( Rank i = _size; r < i; i-- ) //自后向前 
           _elem[i] = _elem[i - 1]; 
    elem[r] = e; _size++; 
    return r;  //置入新元素，更新容量，返回秩
}

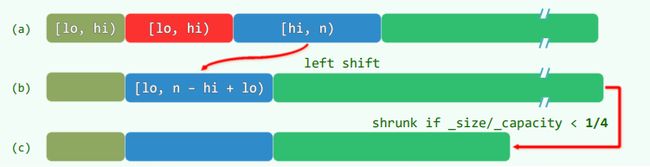
3.区间删除

template int Vector::remove( Rank lo, Rank hi ) { //0<=lo<=hi<=n 
    if ( lo == hi ) return 0; //出于效率考虑，单独处理退化情况 
    while ( hi < _size ) _elem[ lo ++ ] = _elem[ hi ++ ]; 
    _size = lo; 
    shrink(); //更新规模，若有必要则缩容 
    return hi - lo; //返回被删除元素的数目
}

4.单元素删除

template T Vector::remove( Rank r ) { 
    T e = _elem[r]; //备份 
    remove( r, r+1 );  //将单元素视作区间的特例
    return e; //返回被删除元素 
} //O(n-r)

• 每次循环耗时，正比于删除区间的后缀长度n - hi = O(n),而循环次数等于区间宽度 hi - lo = O(n),如此，将导致总体O(n2)的复杂度

5.查找

• 无序向量：判等器

//词条模板类 
template struct Entry { 
    K key; V value; //关键码、数值 
    Entry ( K k = K(), V v = V() ) : key ( k ), value ( v ) {}; //默认构造函数 
    Entry ( Entry const& e ) : key ( e.key ), value ( e.value ) {}; //克隆 
    bool operator== ( Entry const& e ) { return key == e.key; } 
    bool operator!= ( Entry const& e ) { return key != e.key; }   
}

• 有序向量：比较器

template struct Entry {  
    K key; V value; 
    Entry ( K k = K(), V v = V() ) : key ( k ), value ( v ) {}; 
    Entry ( Entry const& e ) : key ( e.key ), value ( e.value ) {}; 
    bool operator== ( Entry const& e ) { return key == e.key; } 
    bool operator!= ( Entry const& e ) { return key != e.key; }  
    bool operator< ( Entry const& e ) { return key < e.key; } 
    bool operator> ( Entry const& e ) { return key > e.key; } 
};

• 得益于比较器和判等器，从此往后，不必严格区分词条及其对应的关键码

• 顺序查找

template Rank Vector:: //O(hi - lo) = O(n) 
find( T const & e, Rank lo, Rank hi ) const { 
    while ( (lo < hi--) && (e != _elem[hi]) ); //逆向查找 
    return hi; //返回值小于lo即意味着失败；否则即命中者的秩（有多个时，返回最大者） 
}

6. 去重（唯一化）

template Rank Vector::deduplicate() { 
    Rank oldSize = _size; 
    for ( Rank i = 1; i < _size; ) 
        if ( find( _elem[i], 0, i ) < 0 ) i++; 
        else remove(i); 
    return oldSize - _size; 
}

7.遍历

• 遍历：对向量中的每一元素，统一实施visit()操作

//函数指针，只读或局部性修改
template<typename T>
void Vector::traverse( void ( * visit )( T & ) ) { 
    for ( Rank i = 0; i < _size; i++ ) visit( _elem[i] ); 
} 
//函数对象，全局性修改更便捷
template<typename T> template<typename VST>  
void Vector::traverse( VST & visit ) { 
    for ( Rank i = 0; i < _size; i++ ) visit( _elem[i] ); 
}

四、有序向量

1.唯一化

1.1 有序性及其甄别

• 有序/无序序列中，任何/总有一对相邻元素顺序/逆序，相邻逆序对的数目，可在一定程度上度量向量的紊乱程度

template void checkOrder ( Vector & V ) { 
    int unsorted = 0; 
    V.traverse( CheckOrder(unsorted, V[0]) ); //统计紧邻逆序对 
    if ( 0 < unsorted ) printf ( "Unsorted with %d adjacent inversion(s)\n", unsorted ); 
    else printf ( "Sorted\n" );
}

• 无序向量经预处理转换为有序向量之后，相关算法多可优化

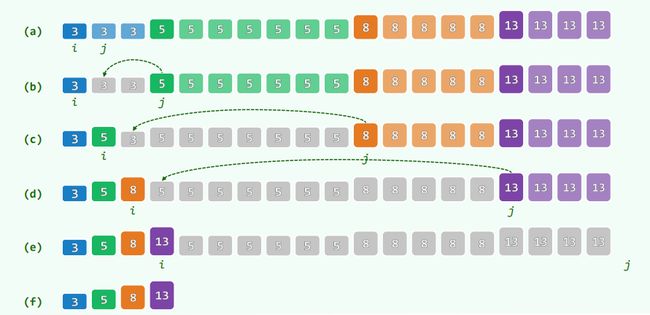
1.2 高效算法

template int Vector::uniquify() { 
    Rank i = 0, j = 0; 
    while ( ++j < _size ) 
        if ( _elem[ i ] != _elem[ j ] ) _elem[ ++i ] = _elem[ j ]; 
    _size = ++i; 
    shrink(); 
    return j - i; 
}

2.二分查找A

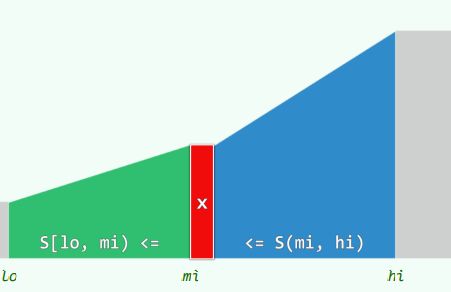
2.1 有序向量中，每个元素都是轴点

• 以任一元素 x = S[mi] 为界，都可将待查找区间[lo,hi)分为三部分,S[lo,mi)≤S[mi]≤S(mi,ho)

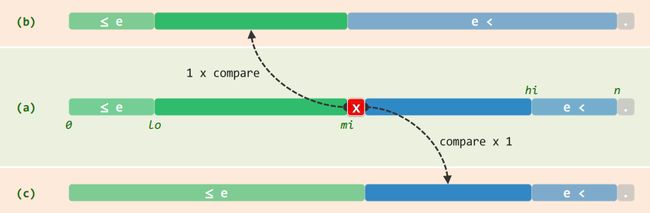
2.2 减而治之

• e < x：则e若存在必属于左侧子区间，故可（减除S[mi,hi)并）递归深入S[lo, mi)

• x < e：则e若存在必属于右侧子区间，亦可（减除S[lo,mi]并）递归深入S(mi, hi)

• e = x：已在此处命中，可随即返回

template<typename T>
static Rank binSearch( T * S, T const & e, Rank lo, Rank hi ) {
    while ( lo < hi ) { //每步迭代可能要做两次比较判断，有三个分支 
        Rank mi = ( lo + hi ) >> 1; //轴点居中（区间宽度折半，等效于其数值右移一位） 
        if ( e < S[mi] ) hi = mi; 
        else if ( S[mi] < e ) lo = mi + 1;  
        else return mi; 
    } 
    return -1; //失败
}

2.3 复杂度

• 线性“递归”:$T(n)=T(n/2)+O(1)=O(\log n)$，大大优于顺序查找

• “递归”跟踪：轴点总能取到中点，递归深度$O(\log n)$；各递归实例仅耗s时O(1)

2.4 关键码的比较次数 ~ 查找长度

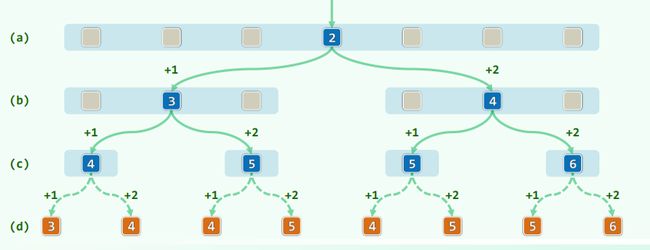
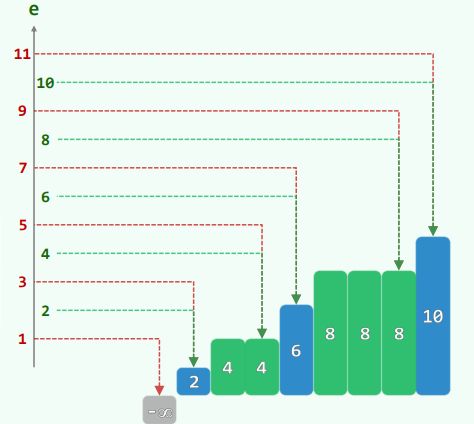
• 成功情况共7种，查找长度分别为 { 4, 3, 5, 2, 5, 4, 6 },等概率情况下，平均 = 29 / 7 = 4.14

• 失败情况共8种，查找长度分别为 {3, 4, 4, 5, 4, 5, 5, 6},等概率情况下，平均 = 36 / 8 = 4.50

3.Fibonacci查找

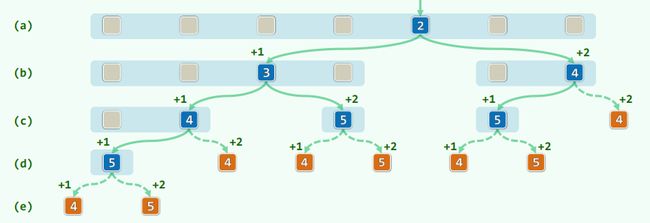
3.1 构思

• 版本A：转向左、右分支前的关键码比较次数不等，而递归深度却相同，通过递归深度的不均衡对转向成本的不均衡做补偿，平均查找长度应能进一步缩短

• 在任何区间[0,n)内，总是选取[λ·n]作为轴点，这类查找算法的渐近复杂度为$\alpha (\lambda )\cdot {\log }_{2}n=O(\log n)$

• 递推式: $\alpha (\lambda )\cdot {\log }_{2}n=\lambda [1+\alpha (\lambda )\cdot {\log }_2(\lambda n)]+(1-\lambda )[2+\alpha (\lambda )\cdot {\log }_2((1-\lambda )n)]$

• 整理后：$$\frac{-\ln 2}{\alpha (\lambda )}$$=$$\frac{\lambda \cdot \ln \lambda +(1-\lambda )\cdot \ln (1-\lambda )}{2-\lambda }$$

• 解：当λ=ϕ=$(\sqrt{5}-1)/2$时，α(λ)=1.440420…达到最小

template<typename T> 
static Rank fibSearch( T * S, T const & e, Rank lo, Rank hi ) { 
    for ( Fib fib(hi - lo); lo < hi; ) { //Fib数列制表备查 
        while ( hi - lo < fib.get() ) fib.prev(); //自后向前顺序查找轴点（分摊O(1)） 
        Rank mi = lo + fib.get() - 1; //确定形如Fib(k) - 1的轴点 
        if ( e < S[mi] ) hi = mi; 
        else if ( S[mi] < e ) lo = mi + 1; 
        else return mi; 
    } 
    return -1; 
}

3.2 复杂度

• 成功情况共7种：(5 + 4 + 3 + 5 + 2 + 5 + 4) / 7 = 28/7 = 4.00

• 失败情况共8种：(4 + 5 + 4 + 4 + 5 + 4 + 5 + 4) / 8 = 35 / 8 = 4.38

4.二分查找B

4.1 改进思路

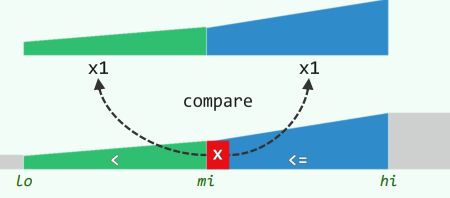
• 二分查找中左、右分支转向代价不平衡的问题，也可直接解决，比如每次迭代仅做1次关键码比较；如此，所有分支只有2个方向，而不再是3个

• 同样地，轴点mi取作中点，则查找每深入一层，问题规模依然会缩减一半

  • e < x：则深入左侧的[lo, mi)

  • x <= e：则深入右侧的[mi, hi)

• 但是直到 hi - lo = 1，才明确判断是否命中，相对于版本A，最好（坏）情况下更坏（好），整体性能更趋均衡
  返回值的语义扩充

4.2 返回值的语义扩充

• 约定总是返回 m = search(e) = M-1 (-∞≤m=max{k|[k]≤e}，min{k|e<[k]}=M≤+∞)

• 实例：V.insert(1+V.search(e),e)

  • 当有多个命中元素时，必须返回最靠后（秩最大）值

  • 失败时，应返回小于e的最大值（含哨兵[lo-1]）

template<typename T> 
static Rank binSearch( T * S, T const & e, Rank lo, Rank hi ) {
    while ( 1 < hi - lo ) { //有效查找区间的宽度缩短至1时，算法才终止 
        Rank mi = (lo + hi) >> 1; 
        e < S[mi] ? hi = mi : lo = mi; 
    } //出口时hi = lo + 1 
    return e == S[lo] ? lo : -1 ;
}

5.二分查找C

template<typename T>
static Rank binSearch( T * S, T const & e, Rank lo, Rank hi ) {
    while ( lo < hi ) {
        Rank mi = (lo + hi) >> 1; 
        e < S[mi] ? hi = mi : lo = mi + 1; /
    } //出口时，区间宽度缩短至0，且必有S[lo = hi] = M 
    return lo - 1; //故，S[lo-1] = m 
}

5.1 与版本B的差异

• 待查找区间宽度缩短至0而非1时，算法才结束

• 转入右侧子向量时，左边界取做mi+1而非mi

• 无论成功与否，返回的秩严格符合接口的语义约定

5.2 正确性

• 不变性：A[0,lo)≤e

• 初始时，lo=0且hi=n，A[0,lo)=A[hi,n)=∅，自然成立

6.插值查找

6.1 原理与算法

• 大数定律：越长的序列，元素的分布越有规律

• [lo, hi]内各元素应大致呈线性趋势增长

  $$\frac{mi-lo}{hi-lo}$$≈$$\frac{e-A[lo]}{A[hi]-A[lo]}$$
  $mi\approx lo+(hi-lo)\cdot \frac{e-A[lo]}{A[hi]-A[lo]}$

6.2 性能

• 最坏：hi-lo=O(n)

• 平均：每经一次比较，待查找区间宽度由n缩至$\sqrt{n}$
  

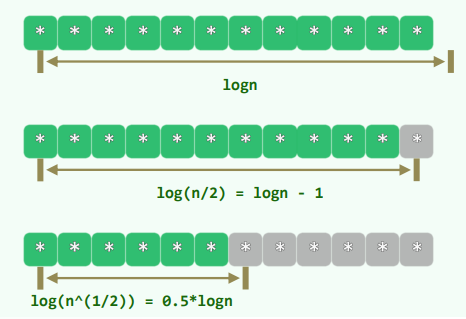
• 每经一次比较,查找区间宽度的数值n开方，有效字长logn减半

  • 插值查找 = 在字长意义上的折半查找
  • 二分查找 = 在字长意义上的顺序查找

6.3 综合评价

• 从O($\log n$)到O($\log \log n$)，优势并不明显（除非查找表极长，或比较操作成本极高）

  • 比如，n = 2⁽²5) = 2^32 = 4G时，log2(n) = 32 - log2(log2(n)) =5

• 须引入乘法、除法运算

• 易受畸形分布的干扰和“蒙骗”

• 实际可行的方法

  • 首先通过插值查找 迅速将查找范围缩小到一定的尺度
  • 然后再进行二分查找 进一步缩小范围
  • 最后（当数据项只有200～300时），使用顺序查找

五、起泡排序

1.构思

• 观察：有序/无序序列中，任何/总有一对相邻元素顺序/逆序

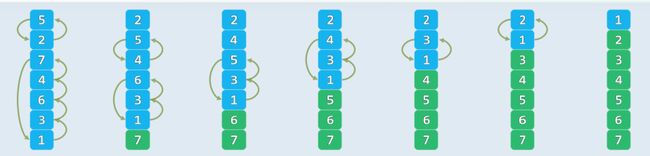
• 扫描交换：依次比较每一对相邻元素；如有必要，交换之，直至某趟扫描后，确认相邻元素均已顺序

template<typename T>
void Vector::bubbleSort( Rank lo, Rank hi ) { 
    while( lo < --hi ) 
        for( Rank i = lo; i < hi; i++ ) 
            if( _elem[i] > _elem[i + 1] ) 
                swap( _elem[i], _elem[i + 1] ); 
}

2.提前终止版

• 有些序列后面部分排序好

template<typename T> void Vector::bubbleSort( Rank lo, Rank hi ) { 
    for( bool sorted = false; sorted = !sorted; hi-- ) 
        for( Rank i = lo + 1; i < hi; i++ ) 
            if( _elem[i-1] > _elem[i] ) 
                swap( _elem[i-1], _elem[i] ), 
                sorted = false; //意味着尚未整体有序
}

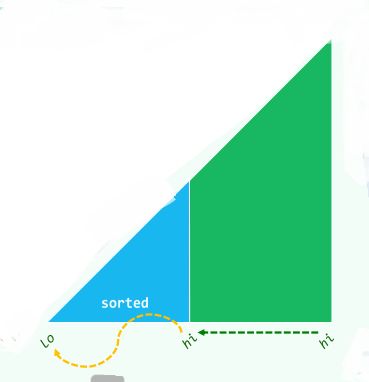
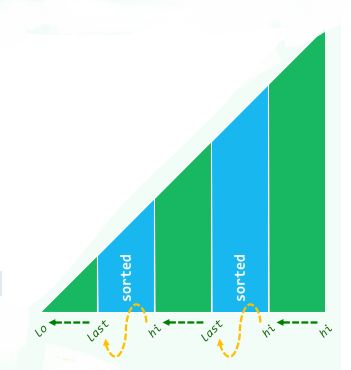
3.跳跃版

• 有些序列已有部分排序好
  

template<typename T> 
void Vector::bubbleSort( Rank lo, Rank hi ) { 
    for( Rank last; lo < hi; hi = last ) 
        for( Rank i = (last = lo) + 1; i < hi; i++ ) 
            if( _elem[i-1] > _elem[i] ) 
                swap( _elem[i-1], _elem[last = i] );
}

4.综合评价

• 时间效率：最好O(n)，最坏O(n2)

• 输入含重复元素时，算法的稳定性（stability）是更为细致的要求

• 起泡排序算法是稳定的,在起泡排序中，唯有相邻元素才可交换

  • 输入： 6, 7a, 3, 2, 7b, 1, 5, 8, 7c, 4
  • 输出： 1, 2, 3, 4, 5, 6, 7a, 7b, 7c, 8

六、归并排序

1.分而治之

template<typename T> 
void Vector::mergeSort( Rank lo, Rank hi ) { 
    if ( hi - lo < 2 ) return; 
    int mi = (lo + hi) >> 1; //O(1)
    mergeSort( lo, mi ); //对前半段排序 T(n/2)
    mergeSort( mi, hi ); //对后半段排序 T(n/2)
    merge( lo, mi, hi ); //归并 O(n)
}

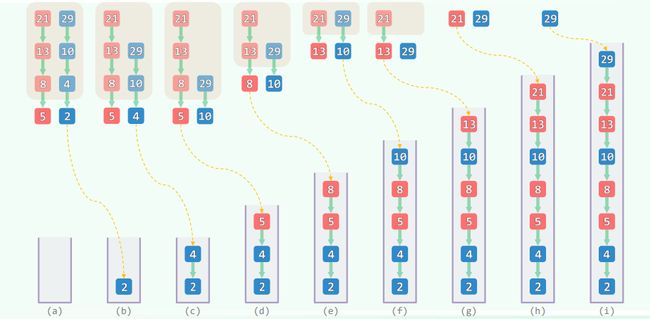
2.二路归并

template<typename T> 
void Vector::merge( Rank lo, Rank mi, Rank hi ) { 
    Rank i = 0; T* A = _elem + lo; 
    Rank j = 0, lb = mi - lo; T* B = new T[lb];
    for ( Rank i = 0; i < lb; i++ ) B[i] = A[i]; //复制自A的前缀 
    Rank k = 0, lc = hi - mi; 
    T* C = _elem + mi;
    while ( ( j < lb ) && ( k < lc ) ) //反复地比较B、C的首元素 
        A[i++] = ( B[j] <= C[k] ) ? B[j++] : C[k++]; //小者优先归入A中 
    while ( j < lb ) A[i++] = B[j++];  //若C先耗尽，则将B残余的后缀归入A中
    delete [] B;
}

3.复杂度

3.1 运行时间

• 二路归并中，两个while循环每迭代一步,i都会递增；j或k中之一也会随之递增。故累计迭代步数 <= lb + lc = n 二路归并只需O(n)时间

• 归并排序的时间复杂度为O(n$\log n$)

3.2 综合评价

• 优点

  • 实现最坏情况下最优 性能的第一个排序算法
  • 不需随机读写，完全顺序访问——尤其适用于列表之类的序列、磁带之类的设备
  • 只要实现恰当，可保证稳定——出现雷同元素时，左侧子向量优先
  • 可扩展性极佳，十分适宜于外部排序——海量网页搜索结果的归并
  • 易于并行化

• 缺点

  • 非就地，需要对等规模的辅助空间
  • 即便输入已是完全（或接近）有序，仍需Ω(n$\log n$)时间

七、位图

1.数据结构

1.1 有限整数组

• ∀0≤k≤U:
  • bool test(int k) k∈S?
  • void set(int k) S∪{k}
  • void clear(int k) S{k}

1.2 结构

class Bitmap { 
private: 
    int N; 
    unsigned char * M; 
    
public: 
    Bitmap( int n = 8 ) { 
        M = new unsigned char[ N = (n+7)/8 ]; 
        memset( M, 0, N ); 
    } 
    ~Bitmap() { 
        delete [] M; 
        M = NULL; 
    } 
    
    void set( int k ); 
    void clear( int k ); 
    bool test( int k ); 
}；

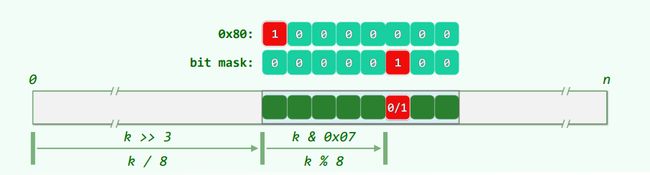
1.3 实现

bool test( int k ) { 
    return M[ k >> 3 ] & ( 0x80 >> (k & 0x07) ); 
} 

void set( int k ) { 
    expand( k ); M[ k >> 3 ] |= ( 0x80 >> (k & 0x07) ); 
} 

void clear( int k ) { 
    expand( k ); M[ k >> 3 ] &= ~( 0x80 >> (k & 0x07) ); 
}

2.典型应用

• 筛法：思路
  

• 筛法：实现

void Eratosthenes( int n, char * file ) { 
    Bitmap B( n ); 
    B.set( 0 ); 
    B.set( 1 ); 
    for ( int i = 2; i < n; i++ ) 
        if ( ! B.test( i ) ) 
            for ( int j = 2*i; j < n; j += i ) 
                B.set( j ); 
    B.dump( file );
}

3.快速初始化

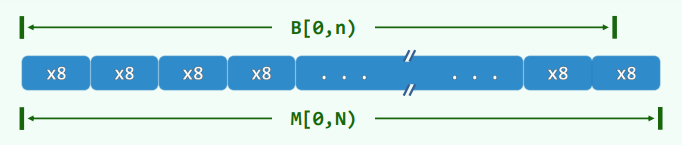
3.1 初始化

• Bitmap的构造函数中，通过 memset(M,0,N) 统一清零，这一步仍等效于诸位清零，时间O(N) = O(n)

• 有时，对于大规模的散列表，初始化的效率直接影响到实际性能

• 有时，甚至会影响到算法的整体渐近复杂度

• 若能省去Bitmap的初始化，则只需 O(n) 时间

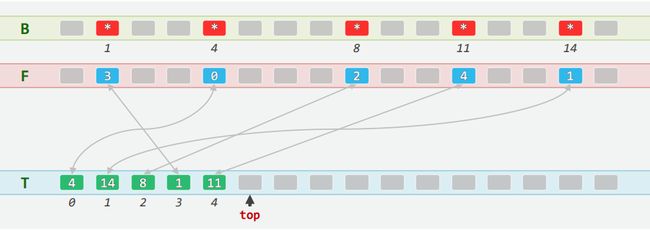
3.2 结构：检验环

• 将B[]拆分成一队等长的Rank型向量，有效位均满足：T[F[k]]=k,F[T[k]]=k
  • Rank F[m]; Form
  • Rank T[m] Rank top=0 To及其栈顶指示