- C语言开发以及维护用到的工具简介
812503533
蓦然回首---再看C语言c语言编辑器开发语言
C语言作为一门经典的编程语言,广泛应用于系统编程、嵌入式开发、操作系统内核等领域。经过第一部分的介绍,已经可以实现一些最简单的功能了,比如文字版本的计算器,猜数字小游戏,通过调整输出格式从而输出优美的图形等等,那么在未来的实际使用中,使用一些什么工具去进行c语言的编辑,查看,编译,运行等等,本文将做简单的介绍,后续再慢慢完善相关的内容。1、编辑器所有语言在编写的时候使用的工具就叫做编辑器,C语言程
- C 语言中的数组详解
812503533
c语言java开发语言
在C语言中,数组是一种非常基础且常用的数据结构。数组是存储一组相同类型元素的集合,允许我们以统一的方式访问和操作这些元素。C语言中的数组不仅在编程中使用广泛,而且它的灵活性和效率使得它成为了许多算法实现的基础。本篇文章将深入分析C语言中的一维数组,包括定义、存储方式、操作方式、常见问题等等,所有的数据结构都可以从这几个方面来学习。1.数组的定义与存储方式1.1一维数组的定义数组的定义方式包括数组大
- C语言回调函数
812503533
c语言java开发语言
前文函数指针中说到了,函数指针的一个重要作用就是实现回调函数,那么什么是回调函数,回调函数有什么作用,在那些场景下使用,具体应该怎么使用,本文就分享下这块的知识。1、回调函数简介回调函数(CallbackFunction)是指将一个函数作为参数传递给另一个函数,然后在适当的时候由被调用的函数执行该回调函数。回调函数是实现事件驱动编程、异步编程和灵活接口设计的核心工具。回调函数通常用于实现高阶函数,
- 暮然回首--再看C语言--常量与宏定义
812503533
蓦然回首---再看C语言c语言
常量与宏定义在C语言中,常量和宏定义是非常重要的概念。它们有助于提高程序的可读性、可维护性,并且能够避免重复代码。常量是指在程序运行期间其值不发生变化的变量,而宏定义是一种预处理指令,用于定义常量或代码片段,在编译阶段进行替换。一、常量常量是指在程序执行过程中其值不可改变的量。在C语言中,我们可以使用const关键字来声明常量。常量分为以下几种类型:常量整数:例如constinta=5;常量浮点数
- C++随机数
宁玉AC
c学习c++开发语言
目录一、名著参考二、详解1.rand()函数2.time(0)3.srand(time(0))4.获取指定范围内的随机数(含指定位数)一、名著参考可以使用cstdlib头文件中的rand()函数来获得随机整数;这个函数返回0~RAND_MAX之间的随机整数;rand()函数生成的是伪随机数。即每次在同一个系统上执行这个函数的时候,rand()函数生成同一序列的数。rand()函数的算法使用一个叫种
- 【C语言】八进制、十六进制
Octopus2077
c语言开发语言算法visualstudio
前言在我们日常生活中使用的数往往是十进制的,而当我们学习C语言后我们会接触到许多不同的进制并且时常需要去思考与使用这些不同的进制(尤其是2的幂相关的进制,因为这种计数系统比十进制更接近于计算机的二进制系统),所以学习和掌握这些不同进制是非常重要的。本文将对八进制和十六进制(8和16都为2的幂)进行一些讲解。通常情况C语言都假定整型常量是十进制的数,但在表达与计算机相关的值时,八进制和十六进制却十分
- 三种优化算法
旅者时光
算法算法python开发语言
本文将总结遗传算法、粒子群算法、模拟退火三种优化算法的核心思路,并使用python完整实现。实际上,越来越多的优秀算法已经被封装为一个易用的接口。很多时候,一行代码就能实现我们的需求。但了解这些算法的基本逻辑,能够使用最基本的代码实现它。无论对于提升我们的编程能力还是解决问题的能力,都会大有裨益。甚至,改变我们思考问题的方式。1、遗传算法遗传算法,顾名思义,就是借鉴了生物通过遗传变异来逐渐适应环境
- 蓝桥杯冲击省一必刷题单(一)
小咖拉眯
蓝桥杯蓝桥杯java算法数据结构
此题单为算法基础精选题单,包含蓝桥杯常考考点以及各种经典算法,可以帮助你打牢基础,查漏补缺。本题单目标是冲击蓝桥杯省一国一,团体程序天梯赛个人国三、XCPC区域赛铜/银奖前言本次题单重点关注日期问题,进制转换问题,排序问题,其中日期问题和进制转换问题,几乎是必考题,几乎每年蓝桥杯都能看到,大家需要重点掌握。日期问题:蓝桥杯热门考点,基本每年省赛必考。进制转换问题:与日期一样蓝桥杯热门考点,基本每年
- Vue3 基础教程:从入门到实践 (保姆级教学)
前段技术人
学习前端vue.jsvue
一、Vue3简介Vue.js是一款用于构建用户界面的JavaScript框架,而Vue3作为其最新的主要版本,带来了诸多令人瞩目的改进与新特性,使其在前端开发领域备受青睐。(一)Vue3的优势性能提升:Vue3重写了虚拟DOM算法,显著提高了挂载、更新和渲染的速度。在处理大型列表或频繁数据更新的场景时,Vue3的表现更为出色,能够为用户带来更流畅的交互体验。例如,一个包含大量商品信息的电商产品列表
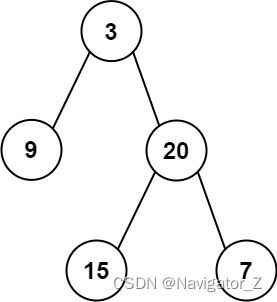
- 刷题前必学!二叉树!用JavaScript学数据结构与算法
JavaScript算法与数据结构-HowieCong务必要熟悉JavaScript使用再来学!一、树是什么?数据结构中的树,对于现实世界中的树简化——树根抽象为“根节点”,树枝抽象为“边”,树枝的两个端点抽象为“结点”,树叶抽象为“叶子结点”计算机中的树如下:二、树的重点树的层次计算规则:根结点所在的那一层为第一层,其子节点为第二层,以此类推结点和树的高度计算规则:叶子结点高度为1,每向上一层
- c语言:操作符
LG.YDX
c语言开发语言
操作符一.算术操作符:+-*%/1.除了%操作符之外,其他的几个操作符可以作用与整数和浮点数,如:5%2.0//error.2.对于操作符,如果两个操作数都为整数,执行整数除法而只要有浮点数执行的就是浮点数除法。3.%操作符的两个操作数必须为整数。二.移位操作符:>1.>右移操作符(移动的是二进制位)右移操作符有两种移动:(1).算术右移,移动的是补码,右边丢弃,左边以和符号位一样的数字进行补位:
- MySQL进阶—— 视图(详解)
1加1等于
MySQLsqlmysql
本文全面介绍Mysql视图相关的核心知识。包括介绍视图定义,基于查询结果的虚拟表,有简化查询、保障安全、解耦逻辑等作用。讲解创建、修改、删除视图的操作,以及及视图可更新条件、安全性控制及性能优化方法。本文目录一、视图的定义与作用定义作用二、视图的创建与管理创建视图修改视图方式1:覆盖原有视图方式2:ALTERVIEW删除视图三、视图两种算法MERGE(默认)TEMPTABLE四、视图的可更新性可更
- Python通过YOLO格式TXT标签文件在图像中画框
CHERISH_KDX
pythonYOLO人工智能
使用场景检测数据集标注是否有误:在目标检测算法中需要标注自己的数据集,为了更加方便的检查数据集标注是否有误,可以使用该工具将标注结果绘制在图像中并查看。美化识别结果中的检测框:在一些目标检测场景中,YOLO检测算法原始的检测框绘制会导致重叠、颜色冲突、字体过大等问题。可以使用该工具进行修改。代码importosimportcv2classcheck_label:def__init__(self,c
- 机器学习之KMeans算法
Mr终游
机器学习机器学习算法kmeans
目录一、KMeans的核心思想二、KMeans算法流程三、KMeans的关键点1.优点:2.缺点:四、如何确定最佳k值1.肘部法则2.轮廓系数五、Kmeans的典型应用场景六、代码示例KMeans是一种广泛使用的无监督学习算法,主要用于聚类分析(Clustering)。它的目标是将数据集划分为K个互不重叠的子集(簇,Cluster),使得同一簇内的数据点尽可能相似,不同簇之间的数据点尽可能差异显著
- 太翌氏文化产业: AGI架构部署
太翌修仙笔录
deepseek第三代人工智能agi架构人工智能
在之前RGOA-重力算法等基础上,分析春秋历日盘排盘驱动行为的ai模式,是否达到AGI标准春秋历日盘排盘驱动行为的AI模式与AGI标准的对比分析一、RGOA-重力算法与春秋历日盘排盘的核心逻辑RGOA算法原理RGOA(GravitationalSearchAlgorithm)是一种基于物理引力定律的优化算法,通过模拟粒子在引力场中的运动来寻找最优解。其核心公式为:Fij=GmimjRij2+ϵ和a
- 聚类分析|k-means聚类方法及其Python实现
皖山文武
数据挖掘商务智能kmeans聚类python数据挖掘机器学习
k-means聚类方法及其Python实现0.k-means算法简介1.k-means算法工作原理2.k-means算法流程3.k–means算法的Python实现0.k-means算法简介k-means算法由MacQueen在1967年提出。是一种经典的基于划分的聚类方法。划分方法(PartitioningMethod)是基于距离判断样本相似度,通过不断迭代将含有多个样本的数据集划分成若干个簇,
- C语言_数据结构总结7:顺序队列(循环队列)
*.✧屠苏隐遥(ノ◕ヮ◕)ノ*.✧
C语言—数据结构数据结构c语言开发语言算法visualstudiovisualstudio
纯C语言实现,不涉及C++队列简称队,也是一种操作受限的线性表。只允许表的一端进行插入,表的另一端进行删除特性:先进先出针对顺序队列存在的“假溢出”问题,引出的循环队列概念。循环队列将顺序队列臆造为一个环状的空间,即把存储队列元素的表从逻辑上视为一个环。当队首指针Q->front=MaxSize-1后,再前进一个位置就自动到0,这可以利用除法取余运算(%)来实现。循环队列中的判空和判满条件分析:显
- 【实战ES】实战 Elasticsearch:快速上手与深度实践-6.2.2GDPR数据脱敏处理
言析数智
实战elasticsearch大数据搜索引擎
点击关注不迷路点击关注不迷路点击关注不迷路文章大纲6.2.2GDPR数据脱敏处理深度实践指南1.GDPR核心要求映射1.1关键条款与技术要求1.2`数据类型与脱敏策略`2.全链路脱敏配置2.1`动态脱敏管道`2.2静态脱敏模板3.`脱敏算法性能对比`3.1算法性能矩阵3.2存储成本分析4.企业级合规方案4.1金融行业案例4.2医疗行业方案5.合规性验证方案5.1自动化检查脚本5.2审计检查清单6.
- C语言--正弦、余弦函数
坚持学习每一天
刘汝佳--算法竞赛入门经典c语言
#include#include#includeintmain(){constdoublepi=acos(-1.0);intn;scanf("%d",&n);printf("%lf%lf",sin(n/180.0*pi),cos(n/180.0*pi));}sin()函数和cos()函数的参数是弧度原型:doublesin(doublex);doublecos(doubley);
- 【贪心算法2】
m0_46150269
贪心算法算法
力扣122.买卖股票最佳时机Ⅱ链接:link思路要求最大利润,可以分解成子问题求解,在最低价格买入,最高价格卖出。假如第0天价格最低,第3天价格最高,利润=prices[3]-pricnes[0],可以将利润公式拆解成(prices[3]-prices[2])+(prices[2]-prices[1])+(prices[1]-prices[0])最终变成了求相邻两天的利润,所以可以得到一个关于利润
- 【贪心算法】柠檬水找零
I_Am_Me_
贪心算法贪心算法算法
1.题目解析860.柠檬水找零-力扣(LeetCode)2.讲解算法原理分情况讨论5---》直接收下10---》找五元,收下20----》10+5△----》5+5+5由于5元更有用,则尽可能保留5元3.代码classSolution{publicbooleanlemonadeChange(int[]bills){intfive=0,ten=0;for(intx:bills){if(x==5){f
- leetcode 贪心算法
gufly-
leetcode贪心算法算法
刷题记录以局部最优推出整体最优,且想不到反例,则可以尝试贪心算法455.分发饼干从后向前遍历孩子数组,用大饼干满足胃口大,并统计满足小孩数量classSolution(object):deffindContentChildren(self,g,s):g.sort()s.sort()res=0ind=len(s)-1foriinrange(len(g)-1,-1,-1):ifind>=0ands[i
- python贪心算法几个经典例子_贪心算法经典例子
weixin_39637979
一、定义什么是贪心算法呢?所谓贪心算法是指,在对问题求解时,总是做出在当前看来最好的选择。也就是说,不从整体最优解出发来考虑,它所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题都能产生整体最优解或整体最优解的近似解。贪心算法的基本思路如下:1.建立数学模型来描述问题。2.把求解的问题分成若干个子问题。3.对每个子问题求解,得到每个子问题的局
- python贪心算法几个经典例子_贪心算法及几个经典例子
weixin_39786850
一、定义什么是贪心算法呢?所谓贪心算法是指,在对问题求解时,总是做出在当前看来最好的选择。也就是说,不从整体最优解出发来考虑,它所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题都能产生整体最优解或整体最优解的近似解。贪心算法的基本思路如下:1.建立数学模型来描述问题。2.把求解的问题分成若干个子问题。3.对每个子问题求解,得到每个子问题的局
- 简单区分 五大算法分析策略(分治、动态规划、贪心、回溯、分支限界)
土味儿~
数据结构与算法数据结构与算法
一、分治法1、设计思想将一个难以直接解决的大问题,分割成k个规模较小的子问题,这些子问题相互独立,且与原问题相同,然后各个击破,分而治之。2、递归算法分治法常常与递归结合使用:通过反复应用分治,可以使子问题与原问题类型一致而规模不断缩小,最终使子问题缩小到很容易求出其解,由此自然导致递归算法。3、子问题规模根据分治法的分割原则,应把原问题分割成多少个子问题才比较适宜?每个子问题是否规模相同或怎样才
- 贪心算法
tzc_fly
白景屹-算法栈贪心算法
贪心算法框架贪心算法(greedyalgorithm)是一个容易想象但难以证明的算法,算法框架包括:可选对象集合S,S是全集;已选对象集合T;判断解是否合法的函数isValid(T);评价解的函数payoff(T);目标:从S中选出T,使isValid(T)为True,同时,满足payoff(T)最大;做法:从空集开始,每次增加一个元素使当前payoff最大最后求解完成需要验证是不是全局最优贪心算
- LeetCode刷题实战522:最长特殊序列 II
编程IT圈
字符串算法leetcodejava数据结构
算法的重要性,我就不多说了吧,想去大厂,就必须要经过基础知识和业务逻辑面试+算法面试。所以,为了提高大家的算法能力,这个公众号后续每天带大家做一道算法题,题目就从LeetCode上面选!今天和大家聊的问题叫做最长特殊序列II,我们先来看题面:https://leetcode-cn.com/problems/longest-uncommon-subsequence-ii/Givenanarrayof
- 贪心算法及几个经典例子
G11176593
贪心算法算法动态规划
贪心算法一、基本概念:所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性,即某个状态以后的过程不会影响以前的状态,只与当前状态有关。所以对所采用的贪心策略一定要仔细
- LeetCode刷题实战:删除字符串中的所有相邻重复项(栈的经典应用)
sprite_雪碧
leetcode算法数据结构
题目描述题目链接:1047.删除字符串中的所有相邻重复项-力扣(LeetCode)给定一个由小写字母组成的字符串s,重复项删除操作会选择两个相邻且相同的字符并删除它们。此操作反复进行,直到无法继续删除。返回最终的字符串。答案保证唯一。输入:s="abbaca"输出:"ca"解释:删除"bb"得到"aaca",再删除"aa"得到"ca"。问题分析与解法思路暴力解法的缺陷最直观的暴力解法是重复扫描字符
- 贪心算法解题框架+经典反例分析,效率提升300%
Reese_Cool
洛谷贪心算法算法c++蓝桥杯
贪心算法是一种在每一步选择中都采取当前状态下的最优决策,从而希望最终达到全局最优解的算法策略。以下从其定义、特点、一般步骤、应用场景及实例等方面进行讲解:定义与基本思想•贪心算法在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解。它通常以自顶向下的方式进行,每一步都选择当前的最优解,而不考虑之前或之后的步骤。特点•无后效性:即
- jsonp 常用util方法
hw1287789687
jsonpjsonp常用方法jsonp callback
jsonp 常用java方法
(1)以jsonp的形式返回:函数名(json字符串)
/***
* 用于jsonp调用
* @param map : 用于构造json数据
* @param callback : 回调的javascript方法名
* @param filters : <code>SimpleBeanPropertyFilter theFilt
- 多线程场景
alafqq
多线程
0
能不能简单描述一下你在java web开发中需要用到多线程编程的场景?0
对多线程有些了解,但是不太清楚具体的应用场景,能简单说一下你遇到的多线程编程的场景吗?
Java多线程
2012年11月23日 15:41 Young9007 Young9007
4
0 0 4
Comment添加评论关注(2)
3个答案 按时间排序 按投票排序
0
0
最典型的如:
1、
- Maven学习——修改Maven的本地仓库路径
Kai_Ge
maven
安装Maven后我们会在用户目录下发现.m2 文件夹。默认情况下,该文件夹下放置了Maven本地仓库.m2/repository。所有的Maven构件(artifact)都被存储到该仓库中,以方便重用。但是windows用户的操作系统都安装在C盘,把Maven仓库放到C盘是很危险的,为此我们需要修改Maven的本地仓库路径。
- placeholder的浏览器兼容
120153216
placeholder
【前言】
自从html5引入placeholder后,问题就来了,
不支持html5的浏览器也先有这样的效果,
各种兼容,之前考虑,今天测试人员逮住不放,
想了个解决办法,看样子还行,记录一下。
【原理】
不使用placeholder,而是模拟placeholder的效果,
大概就是用focus和focusout效果。
【代码】
<scrip
- debian_用iso文件创建本地apt源
2002wmj
Debian
1.将N个debian-506-amd64-DVD-N.iso存放于本地或其他媒介内,本例是放在本机/iso/目录下
2.创建N个挂载点目录
如下:
debian:~#mkdir –r /media/dvd1
debian:~#mkdir –r /media/dvd2
debian:~#mkdir –r /media/dvd3
….
debian:~#mkdir –r /media
- SQLSERVER耗时最长的SQL
357029540
SQL Server
对于DBA来说,经常要知道存储过程的某些信息:
1. 执行了多少次
2. 执行的执行计划如何
3. 执行的平均读写如何
4. 执行平均需要多少时间
列名 &
- com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil
7454103
eclipse
今天eclipse突然报了com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil 错误,并且工程文件打不开了,在网上找了一下资料,然后按照方法操作了一遍,好了,解决方法如下:
错误提示信息:
An error has occurred.See error log for more details.
Reason:
com/genuitec/
- 用正则删除文本中的html标签
adminjun
javahtml正则表达式去掉html标签
使用文本编辑器录入文章存入数据中的文本是HTML标签格式,由于业务需要对HTML标签进行去除只保留纯净的文本内容,于是乎Java实现自动过滤。
如下:
public static String Html2Text(String inputString) {
String htmlStr = inputString; // 含html标签的字符串
String textSt
- 嵌入式系统设计中常用总线和接口
aijuans
linux 基础
嵌入式系统设计中常用总线和接口
任何一个微处理器都要与一定数量的部件和外围设备连接,但如果将各部件和每一种外围设备都分别用一组线路与CPU直接连接,那么连线
- Java函数调用方式——按值传递
ayaoxinchao
java按值传递对象基础数据类型
Java使用按值传递的函数调用方式,这往往使我感到迷惑。因为在基础数据类型和对象的传递上,我就会纠结于到底是按值传递,还是按引用传递。其实经过学习,Java在任何地方,都一直发挥着按值传递的本色。
首先,让我们看一看基础数据类型是如何按值传递的。
public static void main(String[] args) {
int a = 2;
- ios音量线性下降
bewithme
ios音量
直接上代码吧
//second 几秒内下降为0
- (void)reduceVolume:(int)second {
KGVoicePlayer *player = [KGVoicePlayer defaultPlayer];
if (!_flag) {
_tempVolume = player.volume;
- 与其怨它不如爱它
bijian1013
选择理想职业规划
抱怨工作是年轻人的常态,但爱工作才是积极的心态,与其怨它不如爱它。
一般来说,在公司干了一两年后,不少年轻人容易产生怨言,除了具体的埋怨公司“扭门”,埋怨上司无能以外,也有许多人是因为根本不爱自已的那份工作,工作完全成了谋生的手段,跟自已的性格、专业、爱好都相差甚远。
- 一边时间不够用一边浪费时间
bingyingao
工作时间浪费
一方面感觉时间严重不够用,另一方面又在不停的浪费时间。
每一个周末,晚上熬夜看电影到凌晨一点,早上起不来一直睡到10点钟,10点钟起床,吃饭后玩手机到下午一点。
精神还是很差,下午像一直野鬼在城市里晃荡。
为何不尝试晚上10点钟就睡,早上7点就起,时间完全是一样的,把看电影的时间换到早上,精神好,气色好,一天好状态。
控制让自己周末早睡早起,你就成功了一半。
有多少个工作
- 【Scala八】Scala核心二:隐式转换
bit1129
scala
Implicits work like this: if you call a method on a Scala object, and the Scala compiler does not see a definition for that method in the class definition for that object, the compiler will try to con
- sudoku slover in Haskell (2)
bookjovi
haskellsudoku
继续精简haskell版的sudoku程序,稍微改了一下,这次用了8行,同时性能也提高了很多,对每个空格的所有解不是通过尝试算出来的,而是直接得出。
board = [0,3,4,1,7,0,5,0,0,
0,6,0,0,0,8,3,0,1,
7,0,0,3,0,0,0,0,6,
5,0,0,6,4,0,8,0,7,
- Java-Collections Framework学习与总结-HashSet和LinkedHashSet
BrokenDreams
linkedhashset
本篇总结一下两个常用的集合类HashSet和LinkedHashSet。
它们都实现了相同接口java.util.Set。Set表示一种元素无序且不可重复的集合;之前总结过的java.util.List表示一种元素可重复且有序
- 读《研磨设计模式》-代码笔记-备忘录模式-Memento
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
/*
* 备忘录模式的功能是,在不破坏封装性的前提下,捕获一个对象的内部状态,并在对象之外保存这个状态,为以后的状态恢复作“备忘”
- 《RAW格式照片处理专业技法》笔记
cherishLC
PS
注意,这不是教程!仅记录楼主之前不太了解的
一、色彩(空间)管理
作者建议采用ProRGB(色域最广),但camera raw中设为ProRGB,而PS中则在ProRGB的基础上,将gamma值设为了1.8(更符合人眼)
注意:bridge、camera raw怎么设置显示、输出的颜色都是正确的(会读取文件内的颜色配置文件),但用PS输出jpg文件时,必须先用Edit->conv
- 使用 Git 下载 Spring 源码 编译 for Eclipse
crabdave
eclipse
使用 Git 下载 Spring 源码 编译 for Eclipse
1、安装gradle,下载 http://www.gradle.org/downloads
配置环境变量GRADLE_HOME,配置PATH %GRADLE_HOME%/bin,cmd,gradle -v
2、spring4 用jdk8 下载 https://jdk8.java.
- mysql连接拒绝问题
daizj
mysql登录权限
mysql中在其它机器连接mysql服务器时报错问题汇总
一、[running]
[email protected]:~$mysql -uroot -h 192.168.9.108 -p //带-p参数,在下一步进行密码输入
Enter password: //无字符串输入
ERROR 1045 (28000): Access
- Google Chrome 为何打压 H.264
dsjt
applehtml5chromeGoogle
Google 今天在 Chromium 官方博客宣布由于 H.264 编解码器并非开放标准,Chrome 将在几个月后正式停止对 H.264 视频解码的支持,全面采用开放的 WebM 和 Theora 格式。
Google 在博客上表示,自从 WebM 视频编解码器推出以后,在性能、厂商支持以及独立性方面已经取得了很大的进步,为了与 Chromium 现有支持的編解码器保持一致,Chrome
- yii 获取控制器名 和方法名
dcj3sjt126com
yiiframework
1. 获取控制器名
在控制器中获取控制器名: $name = $this->getId();
在视图中获取控制器名: $name = Yii::app()->controller->id;
2. 获取动作名
在控制器beforeAction()回调函数中获取动作名: $name =
- Android知识总结(二)
come_for_dream
android
明天要考试了,速速总结如下
1、Activity的启动模式
standard:每次调用Activity的时候都创建一个(可以有多个相同的实例,也允许多个相同Activity叠加。)
singleTop:可以有多个实例,但是不允许多个相同Activity叠加。即,如果Ac
- 高洛峰收徒第二期:寻找未来的“技术大牛” ——折腾一年,奖励20万元
gcq511120594
工作项目管理
高洛峰,兄弟连IT教育合伙人、猿代码创始人、PHP培训第一人、《细说PHP》作者、软件开发工程师、《IT峰播》主创人、PHP讲师的鼻祖!
首期现在的进程刚刚过半,徒弟们真的很棒,人品都没的说,团结互助,学习刻苦,工作认真积极,灵活上进。我几乎会把他们全部留下来,现在已有一多半安排了实际的工作,并取得了很好的成绩。等他们出徒之日,凭他们的能力一定能够拿到高薪,而且我还承诺过一个徒弟,当他拿到大学毕
- linux expect
heipark
expect
1. 创建、编辑文件go.sh
#!/usr/bin/expect
spawn sudo su admin
expect "*password*" { send "13456\r\n" }
interact
2. 设置权限
chmod u+x go.sh 3.
- Spring4.1新特性——静态资源处理增强
jinnianshilongnian
spring 4.1
目录
Spring4.1新特性——综述
Spring4.1新特性——Spring核心部分及其他
Spring4.1新特性——Spring缓存框架增强
Spring4.1新特性——异步调用和事件机制的异常处理
Spring4.1新特性——数据库集成测试脚本初始化
Spring4.1新特性——Spring MVC增强
Spring4.1新特性——页面自动化测试框架Spring MVC T
- idea ubuntuxia 乱码
liyonghui160com
1.首先需要在windows字体目录下或者其它地方找到simsun.ttf 这个 字体文件。
2.在ubuntu 下可以执行下面操作安装该字体:
sudo mkdir /usr/share/fonts/truetype/simsun
sudo cp simsun.ttf /usr/share/fonts/truetype/simsun
fc-cache -f -v
- 改良程序的11技巧
pda158
技巧
有很多理由都能说明为什么我们应该写出清晰、可读性好的程序。最重要的一点,程序你只写一次,但以后会无数次的阅读。当你第二天回头来看你的代码 时,你就要开始阅读它了。当你把代码拿给其他人看时,他必须阅读你的代码。因此,在编写时多花一点时间,你会在阅读它时节省大量的时间。
让我们看一些基本的编程技巧:
尽量保持方法简短
永远永远不要把同一个变量用于多个不同的
- 300个涵盖IT各方面的免费资源(下)——工作与学习篇
shoothao
创业免费资源学习课程远程工作
工作与生产效率:
A. 背景声音
Noisli:背景噪音与颜色生成器。
Noizio:环境声均衡器。
Defonic:世界上任何的声响都可混合成美丽的旋律。
Designers.mx:设计者为设计者所准备的播放列表。
Coffitivity:这里的声音就像咖啡馆里放的一样。
B. 避免注意力分散
Self Co
- 深入浅出RPC
uule
rpc
深入浅出RPC-浅出篇
深入浅出RPC-深入篇
RPC
Remote Procedure Call Protocol
远程过程调用协议
它是一种通过网络从远程计算机程序上请求服务,而不需要了解底层网络技术的协议。RPC协议假定某些传输协议的存在,如TCP或UDP,为通信程序之间携带信息数据。在OSI网络通信模型中,RPC跨越了传输层和应用层。RPC使得开发