- 密码学,算法在人工智能的实战利用
china—hbaby
人工智能密码学
在人工智能(AI)的快速发展中,数据安全和隐私保护成为了核心议题。密码学,作为保护信息安全的基石,其在AI领域的应用显得尤为重要。本文将探讨密码学在AI中的利用,并提供一些代码示例来展示其实际应用。密码学的概述即常用加密方式密码学(Cryptography)是数学和计算机科学的一个分支,它涉及保护信息的安全性和隐私性。密码学的主要目标是确保信息在传输过程中不被未授权的第三方读取或篡改,以及确保信息
- 力扣算法ing(35 / 100)
菥菥爱嘻嘻
小白学习算法算法leetcodetypescriptjavascript
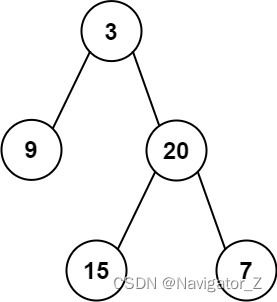
3.22104.二叉树的最大深度我的思路:dfs,深度优先搜索或者说能不能先根搜索,根层数3192nullmax=2202153nullmax=373nullmax=3我的代码:if(head.next===null)maxreturnfunctionmaxDepth(root:TreeNode|null):number{functionfindMax(root:TreeNode|null,dep
- 力扣算法ing(30 / 100)
菥菥爱嘻嘻
小白学习算法算法leetcodetypescriptjavascript
3.1719.删除链表的倒数第n个结点给你一个链表,删除链表的倒数第n个结点,并且返回链表的头结点。示例1:输入:head=[1,2,3,4,5],n=2输出:[1,2,3,5]示例2:输入:head=[1],n=1输出:[]示例3:输入:head=[1,2],n=1输出:[1]删除指定的节点,给出头节点逆转链表,寻找第n个,删除不行不行,逆转录又要反转回去后面我想到了一个解决办法:利用数组计算总
- 力扣算法ing(9/100)
菥菥爱嘻嘻
小白学习算法算法leetcode数据库typescript
2.26438.找到字符串中所有字母的异位词438.找到字符串中所有字母异位词给定两个字符串s和p,找到s中所有p的异位词的子串,返回这些子串的起始索引。不考虑答案输出的顺序。示例1:输入:s="cbaebabacd",p="abc"输出:[0,6]解释:起始索引等于0的子串是"cba",它是"abc"的异位词。起始索引等于6的子串是"bac",它是"abc"的异位词。示例2:输入:s="abab
- 【C/C++】在排序数组中查找元素的第一个和最后一个位置(leetcode T34)
勇士小蓝0727
c语言c++leetcode开发语言算法数据结构蓝桥杯
核心考点:法一双指针法;法二二分查找法题目描述:给你一个按照非递减顺序排列的整数数组nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值target,返回[-1,-1]。你必须设计并实现时间复杂度为O(logn)的算法解决此问题。(示例见文末)答案详解:方法一:双指针法vectorsearchRange(vector&nums,inttarge
- 【C语言初学】C语言中表示次方与开根
JAMJAM_NoName
Cc语言开发语言后端
开根:doublesqrt(doublex)(对x开根)次方:doublepow(doublex,doubley)(计算x^y)上述两个函数都属于math库中使用前要将预处理命令#include包含进源文件中两个例题:1.输入三角形的三边长,求三角形的面积已知三条边长a,b,c三角形面积公式:#include#includeintmain(){doublea,b,c;scanf("%lf%lf%l
- 每日算法题-Nim 游戏 - 台阶
晚夜微雨问海棠呀
算法游戏
给定一个台阶数n,玩家每次可以选择跳跃1到m个台阶,最后一个台阶到达者获胜。假设两位玩家都采取最优策略,判断先手玩家是否会获胜。输入格式一行包含两个整数n和m(1≤n,m≤10^9)。输出格式如果先手玩家能获胜,输出"Yes";否则输出"No"。n,m=map(int,input().split())ifnm时,若n%(m+1)≠0,先手可以通过策略使剩余台阶数变为(m+1)的倍数,将必败态转移给
- 算法每日一练 (17)
张胤尘
算法每日一练算法数据结构
欢迎来到张胤尘的技术站技术如江河,汇聚众志成。代码似星辰,照亮行征程。开源精神长,传承永不忘。携手共前行,未来更辉煌文章目录算法每日一练(17)打家劫舍题目描述解题思路解题代码`c/c++``golang``lua`官方站点:力扣Leetcode算法每日一练(17)打家劫舍题目地址:打家劫舍题目描述你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的
- 算法每日一练 (16)
张胤尘
算法每日一练算法数据结构
欢迎来到张胤尘的技术站技术如江河,汇聚众志成。代码似星辰,照亮行征程。开源精神长,传承永不忘。携手共前行,未来更辉煌文章目录算法每日一练(16)使用最小花费爬楼梯题目描述解题思路解题代码`c/c++``golang``lua`官方站点:力扣Leetcode算法每日一练(16)使用最小花费爬楼梯题目地址:使用最小花费爬楼梯题目描述给你一个整数数组cost,其中cost[i]是从楼梯第i个台阶向上爬需
- 目标检测领域总结:从传统方法到 Transformer 时代的革新
DoYangTan
目标检测系列目标检测transformer人工智能
目标检测领域总结:从传统方法到Transformer时代的革新目标检测是计算机视觉领域的一个核心任务,它的目标是从输入图像中识别并定位出目标物体。随着深度学习的兴起,目标检测方法已经取得了显著的进展。从最早的传统方法到现如今基于Transformer的先进算法,目标检测的发展经历了多个重要的阶段。本文将详细总结目标检测领域的演进,涵盖传统方法、两阶段检测方法、单阶段检测方法和基于Transform
- 2024MathorCup数学建模之——MathorCup奖杯”获得者经验思路分享
美赛数学建模
数学建模
一、经验分享1.工具选择:顺手即可。Matlab和Python都是比较主流的选择,二者的应用场合各有不同。Python在数据分析、深度学习方面的优势愈发明显,而Matlab更适合进行物理仿真和数值计算。不过随着Python社区不断发展,其功能也愈发全面与强大,因此我们比较推荐学有余力的情况下可以更早接触Python。2.模型算法:多多益善。不一定要精通所有的算法,但是手上至少要准备一些常用的算法(
- 1.✨学习系统浅探
*TQK*
自我认知规划(不让别人看)认知提升
不要过于苛求完美,允许自己偶尔放松,保持积极心态。长期坚持比短期高强度更重要,尤其是为三年后的考研做准备,需要持续的努力而不是一时的冲刺。定期复盘,调整计划。如果某天状态不好,可以适当减少任务量,保持弹性。同时,保证足够的睡眠和运动,这对维持多巴胺水平和整体精力很重要。一、系统构建一Deepseek指令我的大一下学期已经开始了,这一学期我又有新的计算机课程。上一学期我学了C语言,基础知识掌握的还可
- AI人工智能软件开发方案:开启智能时代的创新钥匙
广州硅基技术官方
人工智能
一、引言:AI浪潮下的软件开发新机遇近年来,人工智能(AI)技术的迅猛发展如同一股汹涌澎湃的浪潮,席卷了全球各个领域。从最初的概念提出到如今的广泛应用,AI历经了漫长的发展历程,终于迎来了属于它的黄金时代。回首过去,AI的发展并非一帆风顺,早期由于计算能力和算法的限制,经历了多次起伏。但随着大数据、云计算、机器学习、深度学习等技术的不断突破,AI迎来了爆发式增长。如今,AI已经深入到人们生活和工作
- 燃爆!程序员如何借助 AI 大模型冲破编程效率枷锁?(以DeepSeek,ChatGPT为例)
羑悻的小杀马特.
AI学习chatgptdeepseekAI大模型开发语言
AI大模型已成为程序员提升效率的有力助手。本文聚焦DeepSeek和ChatGPT,探讨程序员如何借其冲破编程效率枷锁。在代码编写阶段,它们能快速生成基础框架、实现特定功能及复杂算法代码;调试时,精准分析错误并给出优化建议;文档生成方面,为函数、类及项目文档助力。程序员需掌握高效交互技巧,结合自身经验,合理利用AI大模型,全面提升编程效率,开启高效编程新境界。目录一·本篇背景:二、AI大模型简介2
- Pytorch深度学习教程_9_nn模块构建神经网络
tRNA做科研
深度学习保姆教程深度学习pytorch神经网络
欢迎来到《深度学习保姆教程》系列的第九篇!在前面的几篇中,我们已经介绍了Python、numpy及pytorch的基本使用,进行了梯度及神经网络的实践并学习了激活函数和激活函数,在上一个教程中我们学习了优化算法。今天,我们将开始使用pytorch构建我们自己的神经网络。欢迎订阅专栏进行系统学习:深度学习保姆教程_tRNA做科研的博客-CSDN博客目录1.理解nn模块:(1)使用nn.Sequent
- 【机器学习】算法分类
CH3_CH2_CHO
什么?!是机器学习!!机器学习算法有监督学习无监督学习半监督学习强化学习
1、有监督学习1.1定义使用带标签的数据训练模型。有监督学习是机器学习中最常见的一种类型,它利用已知的输入特征和对应的输出标签来训练模型,使模型能够学习到特征与标签之间的映射关系。在训练过程中,模型会不断地调整自身的参数,以最小化预测值与真实标签之间的误差,从而提高预测的准确性。1.2回归问题1.2.1目标预测连续值。回归问题的目标是预测一个连续的数值结果,模型的输出是一个实数值。1.2.2解释回
- # LeetCode题解:最大正方形面积
小学仔
java动态规划算法leetcode矩阵
##题目描述在一个由`'0'`和`'1'`组成的二维矩阵中,找到只包含`'1'`的最大正方形,并返回其面积。**示例**:```输入:matrix=[["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]输出:4```解释:最大正方形的边长为2,面积为4。---##解题思路##
- LeetCode剑指offer题目记录4
t.y.Tang
LeetCode记录leetcodepython矩阵
leetcode刷题开始啦,每天记录几道题.目录剑指offer07.重建二叉树题目描述示例思路python改进剑指offer09.用两个栈实现队列题目描述示例思路python剑指offer10-1.斐波那契数列题目描述思路pythonC++剑指offer10-2.青蛙跳台阶问题问题描述思路C++剑指offer07.重建二叉树题目描述输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节
- 数据结构——链表专项
seven——seven
linuxmailbox之线程邮箱数据结构链表算法
数据结构的总结1.定义一组用来保存一种或者多种特定关系的数据的集合(组织和存储数据)程序的设计:将现实中大量而复杂的问题以特定的数据类型和特定的存储结构存储在内存中,并在此基础上实现某个特定的功能的操作;程序=数据结构+算法高内聚,低耦合2.数据与数据之间的关系数据的逻辑结构:数据元素与元素之间的关系集合:关系平等线性结构:元素之间一对一的关系(表,队列。栈。。。)树型结构:元素之间一对多的关系(
- Linux内核中的数据结构与算法(三)哈希链表
木木0o0欧尼
Linux链表数据结构linux
四,哈希链表谈到链表就不得不谈Linux内核中另外一个重要的结构,哈希链表。讨论这个结构前,你需要对哈希的最基本的概念要清楚哦,由于我们已经讲过Linux内核中的普通链表的结构,这里我们对比他们的区别来了解哈希链表会直观一些。Linux链表认为双指针表头双循环链表对于HASH表来说过于浪费,因而设计了一套用于HASH表的hlist的数据结构,单指针表头双循环链表。hlish表头仅有一个指向首节点的
- 多种方法判断一个数是否为素数的实现与优化
徐浪老师
徐浪老师大讲堂数据结构算法
素数,又称质数,是一个在数学和计算机科学中非常重要的概念。它是大于1的自然数中,除了1和它本身,不能被其他数整除的数。本文将从最基础的方法讲解到优化算法,并提供完整的实现代码,帮助您高效地判断一个数是否为素数。一、素数的基础知识1.1素数的定义素数:一个大于1的正整数,只有两个正因子:1和它本身。例如:2、3、5、7、11等。非素数:大于1的数中,可以被除1和本身以外的数整除的数。例如:4、6、8
- 代码随想录算法训练营DAY59|110.字符串接龙、105.有向图的完全可达性、106. 岛屿的周长
阿緑
代码随想录打卡算法
110.字符串接龙fromcollectionsimportdequedeffindshortestpath(strlist,beginstr,endstr):que=deque()visited={}que.append(beginstr)visited[beginstr]=1result=0whileque:cur=que.popleft()result=visited[cur]foriinr
- 字符串作为数组和用指针指向的字符串的区别
kfhj
c语言
字符串作为数组和用指针指向的字符串在C语言(以及类似语言如C++)中都有各自的用途和特点。以下是它们之间的主要区别:定义和声明•字符串作为数组:字符串数组是一个字符数组,其中最后一个字符是空字符(’\0’),用于标识字符串的结束。例如:charstr[]=“Hello,World!”;这里,str是一个字符数组,包含了字符串"Hello,World!"和它的结尾空字符。•用指针指向的字符串:字符串
- 基于NanoDet的无人机交通违规监控系统设计与实现
深度学习&目标检测实战项目
NanoDet无人机目标检测人工智能计算机视觉深度学习
1.引言随着无人机技术的发展,无人机在交通监控领域的应用逐渐增多。无人机能够提供空中视角,具有更高的视野覆盖范围,能够帮助交通管理部门实时监控交通违规行为。本博客将介绍如何使用NanoDet模型实现无人机交通违规监控系统,并结合PyQt5设计一个UI界面来实时展示检测结果。通过该系统,能够检测交通违规行为并做出实时预警,确保交通安全。本博客详细介绍了数据集的构建、模型的训练与推理、碰撞检测算法的实
- P3375 【模板】KMP
好好学习^按时吃饭
算法
题目来自洛谷网站:思路:从题目名字知道这是KMP模板题目,对于KMP算法,就两步,1、构造next数组。2、在s1中找到s2出现的位置。KMP代码:#includeusingnamespacestd;constintN=1e6+10;chars1[N],s2[N];//全局变量名字不能定义为next//C++标准库中有一个函数名字是nextintnext1[N];//ne数组intmain(){/
- 代码训练day7哈希表2
徵686
散列表数据结构
1.四数相加IIleetcode454哈希表判断是否存在classSolution{//四数相加ii统计个数publicintfourSumCount(int[]nums1,int[]nums2,int[]nums3,int[]nums4){HashMapmap=newHashMapmagazine.length())returnfalse;//java字符串长度s.length()for(cha
- 机器学习——分类、回归、聚类、LASSO回归、Ridge回归(自用)
代码的建筑师
模型学习模型训练机器学习机器学习分类回归正则化项LASSORidge朴素
纠正自己的误区:机器学习是一个大范围,并不是一个小的方向,比如:线性回归预测、卷积神经网络和强化学都是机器学习算法在不同场景的应用。机器学习最为关键的是要有数据,也就是数据集名词解释:数据集中的一行叫一条样本或者实例,列名称为特征或者属性。样本的数量称为数据量,特征的数量称为特征维度机器学习常用库:Numpy和sklearn朴素的意思是特征的各条件都是相互独立的机器学习(模型、策略、算法)损失函数
- 量化交易系统中如何处理机器学习模型的训练和部署?
openwin_top
量化交易系统开发机器学习人工智能量化交易
microPythonPython最小内核源码解析NI-motion运动控制c语言示例代码解析python编程示例系列python编程示例系列二python的Web神器Streamlit如何应聘高薪职位量化交易系统中,机器学习模型的训练和部署需要遵循一套严密的流程,以确保模型的可靠性、性能和安全性。以下是详细描述以及相关的示例:1.数据收集和预处理数据收集在量化交易中,数据是最重要的资产。收集的数
- 异步编程中的并发编程优化
AI天才研究院
架构师必知必会系列自然语言处理人工智能语言模型编程实践开发语言架构设计
文章目录1.简介2.基本概念术语说明什么是异步编程?为什么要异步编程?浅谈异步编程模型基于事件驱动的模型基于消息队列的模型基于协程的模型为什么要进行并发优化?3.基本算法原理和具体操作步骤1.串行执行2.并行执行3.任务分片4.超时重试5.异步回调6.消息队列7.缓存8.异步框架9.模型选择4.具体代码实例和解释说明模块划分1.串行执行2.并行执行3.任务分片4.超时重试5.异步回调6.消息队列7
- 算法训练(leetcode)第四十六天 | 110. 字符串接龙、105. 有向图的完全可达性、106. 岛屿的周长
Star Patrick
刷题日记算法leetcode职场和发展
刷题记录*110.字符串接龙105.有向图的完全可达性邻接矩阵邻接表106.岛屿的周长深搜简化代码*110.字符串接龙题目地址使用广搜。本题相当于求最短路径,因此使用广搜。如何应用广搜是一个难点,因为题目给的是字符串而非图的表示(邻接矩阵、邻接表),因此需要自行构建连接关系。题目要求每一步只能修改一个字符,因此从起始字符串开始,对字符串中的每一个字符进行修改,修改后在输入的字符串列表中查找是否存在
- scala的option和some
矮蛋蛋
编程scala
原文地址:
http://blog.sina.com.cn/s/blog_68af3f090100qkt8.html
对于学习 Scala 的 Java™ 开发人员来说,对象是一个比较自然、简单的入口点。在 本系列 前几期文章中,我介绍了 Scala 中一些面向对象的编程方法,这些方法实际上与 Java 编程的区别不是很大。我还向您展示了 Scala 如何重新应用传统的面向对象概念,找到其缺点
- NullPointerException
Cb123456
androidBaseAdapter
java.lang.NullPointerException: Attempt to invoke virtual method 'int android.view.View.getImportantForAccessibility()' on a null object reference
出现以上异常.然后就在baidu上
- PHP使用文件和目录
天子之骄
php文件和目录读取和写入php验证文件php锁定文件
PHP使用文件和目录
1.使用include()包含文件
(1):使用include()从一个被包含文档返回一个值
(2):在控制结构中使用include()
include_once()函数需要一个包含文件的路径,此外,第一次调用它的情况和include()一样,如果在脚本执行中再次对同一个文件调用,那么这个文件不会再次包含。
在php.ini文件中设置
- SQL SELECT DISTINCT 语句
何必如此
sql
SELECT DISTINCT 语句用于返回唯一不同的值。
SQL SELECT DISTINCT 语句
在表中,一个列可能会包含多个重复值,有时您也许希望仅仅列出不同(distinct)的值。
DISTINCT 关键词用于返回唯一不同的值。
SQL SELECT DISTINCT 语法
SELECT DISTINCT column_name,column_name
F
- java冒泡排序
3213213333332132
java冒泡排序
package com.algorithm;
/**
* @Description 冒泡
* @author FuJianyong
* 2015-1-22上午09:58:39
*/
public class MaoPao {
public static void main(String[] args) {
int[] mao = {17,50,26,18,9,10
- struts2.18 +json,struts2-json-plugin-2.1.8.1.jar配置及问题!
7454103
DAOspringAjaxjsonqq
struts2.18 出来有段时间了! (貌似是 稳定版)
闲时研究下下! 貌似 sruts2 搭配 json 做 ajax 很吃香!
实践了下下! 不当之处请绕过! 呵呵
网上一大堆 struts2+json 不过大多的json 插件 都是 jsonplugin.34.jar
strut
- struts2 数据标签说明
darkranger
jspbeanstrutsservletScheme
数据标签主要用于提供各种数据访问相关的功能,包括显示一个Action里的属性,以及生成国际化输出等功能
数据标签主要包括:
action :该标签用于在JSP页面中直接调用一个Action,通过指定executeResult参数,还可将该Action的处理结果包含到本页面来。
bean :该标签用于创建一个javabean实例。如果指定了id属性,则可以将创建的javabean实例放入Sta
- 链表.简单的链表节点构建
aijuans
编程技巧
/*编程环境WIN-TC*/ #include "stdio.h" #include "conio.h"
#define NODE(name, key_word, help) \ Node name[1]={{NULL, NULL, NULL, key_word, help}}
typedef struct node { &nbs
- tomcat下jndi的三种配置方式
avords
tomcat
jndi(Java Naming and Directory Interface,Java命名和目录接口)是一组在Java应用中访问命名和目录服务的API。命名服务将名称和对象联系起来,使得我们可以用名称
访问对象。目录服务是一种命名服务,在这种服务里,对象不但有名称,还有属性。
tomcat配置
- 关于敏捷的一些想法
houxinyou
敏捷
从网上看到这样一句话:“敏捷开发的最重要目标就是:满足用户多变的需求,说白了就是最大程度的让客户满意。”
感觉表达的不太清楚。
感觉容易被人误解的地方主要在“用户多变的需求”上。
第一种多变,实际上就是没有从根本上了解了用户的需求。用户的需求实际是稳定的,只是比较多,也比较混乱,用户一般只能了解自己的那一小部分,所以没有用户能清楚的表达出整体需求。而由于各种条件的,用户表达自己那一部分时也有
- 富养还是穷养,决定孩子的一生
bijian1013
教育人生
是什么决定孩子未来物质能否丰盛?为什么说寒门很难出贵子,三代才能出贵族?真的是父母必须有钱,才能大概率保证孩子未来富有吗?-----作者:@李雪爱与自由
事实并非由物质决定,而是由心灵决定。一朋友富有而且修养气质很好,兄弟姐妹也都如此。她的童年时代,物质上大家都很贫乏,但妈妈总是保持生活中的美感,时不时给孩子们带回一些美好小玩意,从来不对孩子传递生活艰辛、金钱来之不易、要懂得珍惜
- oracle 日期时间格式转化
征客丶
oracle
oracle 系统时间有 SYSDATE 与 SYSTIMESTAMP;
SYSDATE:不支持毫秒,取的是系统时间;
SYSTIMESTAMP:支持毫秒,日期,时间是给时区转换的,秒和毫秒是取的系统的。
日期转字符窜:
一、不取毫秒:
TO_CHAR(SYSDATE, 'YYYY-MM-DD HH24:MI:SS')
简要说明,
YYYY 年
MM 月
- 【Scala六】分析Spark源代码总结的Scala语法四
bit1129
scala
1. apply语法
FileShuffleBlockManager中定义的类ShuffleFileGroup,定义:
private class ShuffleFileGroup(val shuffleId: Int, val fileId: Int, val files: Array[File]) {
...
def apply(bucketId
- Erlang中有意思的bug
bookjovi
erlang
代码中常有一些很搞笑的bug,如下面的一行代码被调用两次(Erlang beam)
commit f667e4a47b07b07ed035073b94d699ff5fe0ba9b
Author: Jovi Zhang <
[email protected]>
Date: Fri Dec 2 16:19:22 2011 +0100
erts:
- 移位打印10进制数转16进制-2008-08-18
ljy325
java基础
/**
* Description 移位打印10进制的16进制形式
* Creation Date 15-08-2008 9:00
* @author 卢俊宇
* @version 1.0
*
*/
public class PrintHex {
// 备选字符
static final char di
- 读《研磨设计模式》-代码笔记-组合模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
abstract class Component {
public abstract void printStruct(Str
- 利用cmd命令将.class文件打包成jar
chenyu19891124
cmdjar
cmd命令打jar是如下实现:
在运行里输入cmd,利用cmd命令进入到本地的工作盘符。(如我的是D盘下的文件有此路径 D:\workspace\prpall\WEB-INF\classes)
现在是想把D:\workspace\prpall\WEB-INF\classes路径下所有的文件打包成prpall.jar。然后继续如下操作:
cd D: 回车
cd workspace/prpal
- [原创]JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
comsci
eclipse设计模式算法工作swing
JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
&nb
- SecureCRT右键粘贴的设置
daizj
secureCRT右键粘贴
一般都习惯鼠标右键自动粘贴的功能,对于SecureCRT6.7.5 ,这个功能也已经是默认配置了。
老版本的SecureCRT其实也有这个功能,只是不是默认设置,很多人不知道罢了。
菜单:
Options->Global Options ...->Terminal
右边有个Mouse的选项块。
Copy on Select
Paste on Right/Middle
- Linux 软链接和硬链接
dongwei_6688
linux
1.Linux链接概念Linux链接分两种,一种被称为硬链接(Hard Link),另一种被称为符号链接(Symbolic Link)。默认情况下,ln命令产生硬链接。
【硬连接】硬连接指通过索引节点来进行连接。在Linux的文件系统中,保存在磁盘分区中的文件不管是什么类型都给它分配一个编号,称为索引节点号(Inode Index)。在Linux中,多个文件名指向同一索引节点是存在的。一般这种连
- DIV底部自适应
dcj3sjt126com
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- Centos6.5使用yum安装mysql——快速上手必备
dcj3sjt126com
mysql
第1步、yum安装mysql
[root@stonex ~]# yum -y install mysql-server
安装结果:
Installed:
mysql-server.x86_64 0:5.1.73-3.el6_5 &nb
- 如何调试JDK源码
frank1234
jdk
相信各位小伙伴们跟我一样,想通过JDK源码来学习Java,比如collections包,java.util.concurrent包。
可惜的是sun提供的jdk并不能查看运行中的局部变量,需要重新编译一下rt.jar。
下面是编译jdk的具体步骤:
1.把C:\java\jdk1.6.0_26\sr
- Maximal Rectangle
hcx2013
max
Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing all ones and return its area.
public class Solution {
public int maximalRectangle(char[][] matrix)
- Spring MVC测试框架详解——服务端测试
jinnianshilongnian
spring mvc test
随着RESTful Web Service的流行,测试对外的Service是否满足期望也变的必要的。从Spring 3.2开始Spring了Spring Web测试框架,如果版本低于3.2,请使用spring-test-mvc项目(合并到spring3.2中了)。
Spring MVC测试框架提供了对服务器端和客户端(基于RestTemplate的客户端)提供了支持。
&nbs
- Linux64位操作系统(CentOS6.6)上如何编译hadoop2.4.0
liyong0802
hadoop
一、准备编译软件
1.在官网下载jdk1.7、maven3.2.1、ant1.9.4,解压设置好环境变量就可以用。
环境变量设置如下:
(1)执行vim /etc/profile
(2)在文件尾部加入:
export JAVA_HOME=/home/spark/jdk1.7
export MAVEN_HOME=/ho
- StatusBar 字体白色
pangyulei
status
[[UIApplication sharedApplication] setStatusBarStyle:UIStatusBarStyleLightContent];
/*you'll also need to set UIViewControllerBasedStatusBarAppearance to NO in the plist file if you use this method
- 如何分析Java虚拟机死锁
sesame
javathreadoracle虚拟机jdbc
英文资料:
Thread Dump and Concurrency Locks
Thread dumps are very useful for diagnosing synchronization related problems such as deadlocks on object monitors. Ctrl-\ on Solaris/Linux or Ctrl-B
- 位运算简介及实用技巧(一):基础篇
tw_wangzhengquan
位运算
http://www.matrix67.com/blog/archives/263
去年年底写的关于位运算的日志是这个Blog里少数大受欢迎的文章之一,很多人都希望我能不断完善那篇文章。后来我看到了不少其它的资料,学习到了更多关于位运算的知识,有了重新整理位运算技巧的想法。从今天起我就开始写这一系列位运算讲解文章,与其说是原来那篇文章的follow-up,不如说是一个r
- jsearch的索引文件结构
yangshangchuan
搜索引擎jsearch全文检索信息检索word分词
jsearch是一个高性能的全文检索工具包,基于倒排索引,基于java8,类似于lucene,但更轻量级。
jsearch的索引文件结构定义如下:
1、一个词的索引由=分割的三部分组成: 第一部分是词 第二部分是这个词在多少