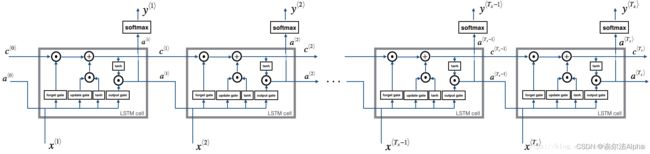
无框架的底层代码实现普通RNN、LSTM的正反向传播过程及应用

1.准备

首先导入所需要的包rnn_utils.py:

import numpy as np

def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum(axis=0)


def sigmoid(x):
    return 1 / (1 + np.exp(-x))

'''
def initialize_adam(parameters) :
    """
    Initializes v and s as two python dictionaries with:
                - keys: "dW1", "db1", ..., "dWL", "dbL" 
                - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
    
    Arguments:
    parameters -- python dictionary containing your parameters.
                    parameters["W" + str(l)] = Wl
                    parameters["b" + str(l)] = bl
    
    Returns: 
    v -- python dictionary that will contain the exponentially weighted average of the gradient.
                    v["dW" + str(l)] = ...
                    v["db" + str(l)] = ...
    s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
                    s["dW" + str(l)] = ...
                    s["db" + str(l)] = ...

    """
    
    L = len(parameters) // 2 # number of layers in the neural networks
    v = {}
    s = {}
    
    # Initialize v, s. Input: "parameters". Outputs: "v, s".
    for l in range(L):
    ### START CODE HERE ### (approx. 4 lines)
        v["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
        v["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
        s["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
        s["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
    ### END CODE HERE ###
    
    return v, s

'''
    
def initialize_adam(parameters):
    """
    初始化v和s，它们都是字典类型的变量，都包含了以下字段：
        - keys: "dW1", "db1", ..., "dWL", "dbL" 
        - values：与对应的梯度/参数相同维度的值为零的numpy矩阵

    参数：
        parameters - 包含了以下参数的字典变量：
            parameters["W" + str(l)] = Wl
            parameters["b" + str(l)] = bl
    返回：
        v - 包含梯度的指数加权平均值，字段如下：
            v["dW" + str(l)] = ...
            v["db" + str(l)] = ...
        s - 包含平方梯度的指数加权平均值，字段如下：
            s["dW" + str(l)] = ...
            s["db" + str(l)] = ...

    """

    L = len(parameters) // 2
    v = {}
    s = {}

    for l in range(L):
        v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])

        s["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
        s["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])

    return (v,s)

'''
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
                                beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8):
    """
    Update parameters using Adam
    
    Arguments:
    parameters -- python dictionary containing your parameters:
                    parameters['W' + str(l)] = Wl
                    parameters['b' + str(l)] = bl
    grads -- python dictionary containing your gradients for each parameters:
                    grads['dW' + str(l)] = dWl
                    grads['db' + str(l)] = dbl
    v -- Adam variable, moving average of the first gradient, python dictionary
    s -- Adam variable, moving average of the squared gradient, python dictionary
    learning_rate -- the learning rate, scalar.
    beta1 -- Exponential decay hyperparameter for the first moment estimates 
    beta2 -- Exponential decay hyperparameter for the second moment estimates 
    epsilon -- hyperparameter preventing division by zero in Adam updates

    Returns:
    parameters -- python dictionary containing your updated parameters 
    v -- Adam variable, moving average of the first gradient, python dictionary
    s -- Adam variable, moving average of the squared gradient, python dictionary
    """
    
    L = len(parameters) // 2                 # number of layers in the neural networks
    v_corrected = {}                         # Initializing first moment estimate, python dictionary
    s_corrected = {}                         # Initializing second moment estimate, python dictionary
    
    # Perform Adam update on all parameters
    for l in range(L):
        # Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".
        ### START CODE HERE ### (approx. 2 lines)
        v["dW" + str(l+1)] = beta1 * v["dW" + str(l+1)] + (1 - beta1) * grads["dW" + str(l+1)] 
        v["db" + str(l+1)] = beta1 * v["db" + str(l+1)] + (1 - beta1) * grads["db" + str(l+1)] 
        ### END CODE HERE ###

        # Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".
        ### START CODE HERE ### (approx. 2 lines)
        v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)] / (1 - beta1**t)
        v_corrected["db" + str(l+1)] = v["db" + str(l+1)] / (1 - beta1**t)
        ### END CODE HERE ###

        # Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".
        ### START CODE HERE ### (approx. 2 lines)
        s["dW" + str(l+1)] = beta2 * s["dW" + str(l+1)] + (1 - beta2) * (grads["dW" + str(l+1)] ** 2)
        s["db" + str(l+1)] = beta2 * s["db" + str(l+1)] + (1 - beta2) * (grads["db" + str(l+1)] ** 2)
        ### END CODE HERE ###

        # Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".
        ### START CODE HERE ### (approx. 2 lines)
        s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)] / (1 - beta2 ** t)
        s_corrected["db" + str(l+1)] = s["db" + str(l+1)] / (1 - beta2 ** t)
        ### END CODE HERE ###

        # Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".
        ### START CODE HERE ### (approx. 2 lines)
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * v_corrected["dW" + str(l+1)] / np.sqrt(s_corrected["dW" + str(l+1)] + epsilon)
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * v_corrected["db" + str(l+1)] / np.sqrt(s_corrected["db" + str(l+1)] + epsilon)
        ### END CODE HERE ###

    return parameters, v, s

'''
def update_parameters_with_adam(parameters,grads,v,s,t,learning_rate=0.01,beta1=0.9,beta2=0.999,epsilon=1e-8):
    """
    使用Adam更新参数

    参数：
        parameters - 包含了以下字段的字典：
            parameters['W' + str(l)] = Wl
            parameters['b' + str(l)] = bl
        grads - 包含了梯度值的字典，有以下key值：
            grads['dW' + str(l)] = dWl
            grads['db' + str(l)] = dbl
        v - Adam的变量，第一个梯度的移动平均值，是一个字典类型的变量
        s - Adam的变量，平方梯度的移动平均值，是一个字典类型的变量
        t - 当前迭代的次数
        learning_rate - 学习率
        beta1 - 动量，超参数,用于第一阶段，使得曲线的Y值不从0开始（参见天气数据的那个图）
        beta2 - RMSprop的一个参数，超参数
        epsilon - 防止除零操作（分母为0）

    返回：
        parameters - 更新后的参数
        v - 第一个梯度的移动平均值，是一个字典类型的变量
        s - 平方梯度的移动平均值，是一个字典类型的变量
    """
    L = len(parameters) // 2
    v_corrected = {} #偏差修正后的值
    s_corrected = {} #偏差修正后的值

    for l in range(L):
        #梯度的移动平均值,输入："v , grads , beta1",输出：" v "
        v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * grads["dW" + str(l + 1)]
        v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads["db" + str(l + 1)]

        #计算第一阶段的偏差修正后的估计值，输入"v , beta1 , t" , 输出："v_corrected"
        v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - np.power(beta1,t))
        v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1,t))

        #计算平方梯度的移动平均值，输入："s, grads , beta2"，输出："s"
        s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * np.square(grads["dW" + str(l + 1)])
        s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.square(grads["db" + str(l + 1)])

        #计算第二阶段的偏差修正后的估计值，输入："s , beta2 , t"，输出："s_corrected"
        s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2,t))
        s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2,t))

        #更新参数，输入: "parameters, learning_rate, v_corrected, s_corrected, epsilon". 输出: "parameters".
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * (v_corrected["dW" + str(l + 1)] / np.sqrt(s_corrected["dW" + str(l + 1)] + epsilon))
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * (v_corrected["db" + str(l + 1)] / np.sqrt(s_corrected["db" + str(l + 1)] + epsilon))

    return (parameters,v,s)

2.RNN

2.1 RNN单元的构建

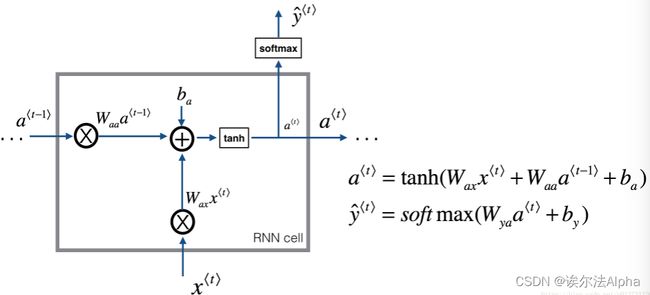
如图为一个RNN单元，通过当前时间步的输入与上一个单元输出的激活值得到本次时间步的预测输出与激活值。通常每个单元还有个cache$(a^{⟨t⟩},a^{⟨t⟩-1},x^{⟨t⟩},parameters)$在反向传播的梯度更新时作为参数使用，与CNN的过程类似。
下面为构建一个Rnn单元的代码：
我们将向量化$m$个样本，因此，$x^{⟨t⟩}$的维度为$(n_x,m)$，$a^{⟨t⟩}$的维度为$(n_a,m)$

mport numpy as np
import rnn_utils


def rnn_cell_forward(xt, a_prev, parameters):
    """
    根据上图实现RNN单元的单步前向传播
    
    参数：
        xt -- 时间步“t”输入的数据，维度为（n_x, m）
        a_prev -- 时间步“t - 1”的隐藏隐藏状态，维度为（n_a, m）
        parameters -- 字典，包含了以下内容:
                        Wax -- 矩阵，输入乘以权重，维度为（n_a, n_x）
                        Waa -- 矩阵，隐藏状态乘以权重，维度为（n_a, n_a）
                        Wya -- 矩阵，隐藏状态与输出相关的权重矩阵，维度为（n_y, n_a）
                        ba  -- 偏置，维度为（n_a, 1）
                        by  -- 偏置，隐藏状态与输出相关的偏置，维度为（n_y, 1）
    
    返回：
        a_next -- 下一个隐藏状态，维度为（n_a， m）
        yt_pred -- 在时间步“t”的预测，维度为（n_y， m）
        cache -- 反向传播需要的元组，包含了(a_next, a_prev, xt, parameters)
    """
    
    # 从“parameters”获取参数
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]
    
    # 使用上面的公式计算下一个激活值
    a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
    
    # 使用上面的公式计算当前单元的输出
    yt_pred = rnn_utils.softmax(np.dot(Wya, a_next) + by)
    
    # 保存反向传播需要的值
    cache = (a_next, a_prev, xt, parameters)
    
    return a_next, yt_pred, cache

随机生成输入值进行测试：

np.random.seed(1)
xt = np.random.randn(3,10)
a_prev = np.random.randn(5,10)
Waa = np.random.randn(5,5)
Wax = np.random.randn(5,3)
Wya = np.random.randn(2,5)
ba = np.random.randn(5,1)
by = np.random.randn(2,1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}

a_next, yt_pred, cache = rnn_cell_forward(xt, a_prev, parameters)
print("a_next[4] = ", a_next[4])  # 随机输出一个查看
print("a_next.shape = ", a_next.shape)
print("yt_pred[1] =", yt_pred[1])
print("yt_pred.shape = ", yt_pred.shape)

测试结果：

a_next[4] =  [ 0.59584544  0.18141802  0.61311866  0.99808218  0.85016201  0.99980978
 -0.18887155  0.99815551  0.6531151   0.82872037]
a_next.shape =  (5, 10)
yt_pred[1] = [0.9888161  0.01682021 0.21140899 0.36817467 0.98988387 0.88945212
 0.36920224 0.9966312  0.9982559  0.17746526]
yt_pred.shape =  (2, 10)

2.2 RNN的前向传播

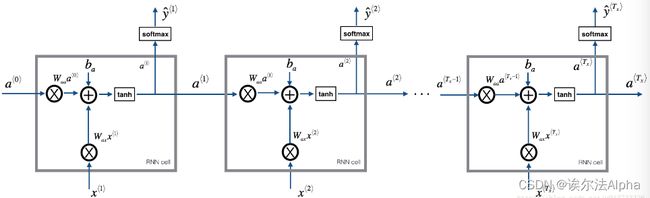
基本的RNN，序列 $x=(x^{⟨1⟩},x^{⟨2⟩},...,x^{⟨T_x⟩})$ 输入$T_x$时间步，输出 $y=(y^{⟨1⟩},y^{⟨2⟩},...,y^{⟨T_x⟩})$。
因为是将多个单元连在一起，所以输入数据x样本单个单元的输入多了一个单元数的维度T_x(n_x, m, T_x)。

def rnn_forward(x, a0, parameters):
    """
    根据上图来实现循环神经网络的前向传播

    参数：
        x -- 输入的全部数据，维度为(n_x, m, T_x)
        a0 -- 初始化隐藏状态，维度为 (n_a, m)
        parameters -- 字典，包含了以下内容:
                        Wax -- 矩阵，输入乘以权重，维度为（n_a, n_x）
                        Waa -- 矩阵，隐藏状态乘以权重，维度为（n_a, n_a）
                        Wya -- 矩阵，隐藏状态与输出相关的权重矩阵，维度为（n_y, n_a）
                        ba  -- 偏置，维度为（n_a, 1）
                        by  -- 偏置，隐藏状态与输出相关的偏置，维度为（n_y, 1）

    返回：
        a -- 所有时间步的隐藏状态，维度为(n_a, m, T_x)
        y_pred -- 所有时间步的预测，维度为(n_y, m, T_x)
        caches -- 为反向传播的保存的元组，维度为（【列表类型】cache, x)
    """

    # 初始化“caches”，它将以列表类型包含所有的cache
    caches = []

    # 获取 x 与 Wya 的维度信息
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wya"].shape

    # 使用0来初始化“a” 与“y”
    a = np.zeros([n_a, m, T_x])
    y_pred = np.zeros([n_y, m, T_x])

    # 初始化“next”
    a_next = a0

    # 遍历所有时间步
    for t in range(T_x):
        ## 1.使用rnn_cell_forward函数来更新“next”隐藏状态与cache。
        # 这里的a_next，在=右边其实是a，在=左边是a，用一个变量名代替
        a_next, yt_pred, cache = rnn_cell_forward(x[:, :, t], a_next, parameters)

        ## 2.使用 a 来保存“next”隐藏状态（第 t ）个位置。
        a[:, :, t] = a_next

        ## 3.使用 y 来保存预测值。
        y_pred[:, :, t] = yt_pred

        ## 4.把cache保存到“caches”列表中。
        caches.append(cache)

    # 保存反向传播所需要的参数
    caches = (caches, x)

    return a, y_pred, caches

进行测试：

np.random.seed(1)
x = np.random.randn(3, 10, 4)
a0 = np.random.randn(5, 10)
Waa = np.random.randn(5, 5)
Wax = np.random.randn(5, 3)
Wya = np.random.randn(2, 5)
ba = np.random.randn(5, 1)
by = np.random.randn(2, 1)
parameters = {"Waa": Waa, "Wax": Wax, "Wya": Wya, "ba": ba, "by": by}

a, y_pred, caches = rnn_forward(x, a0, parameters)
print("a[4][1] = ", a[4][1])  # 取所有时间步的随机一个样本的随机一个激活值
print("a.shape = ", a.shape)
print("y_pred[1][3] =", y_pred[1][3])   # 取所有时间步的随机一个样本的随机一个预测值
print("y_pred.shape = ", y_pred.shape)
print("caches[1][1][3] =", caches[1][1][3])    # 取所有时间步的随机一个样本的随机一个样本值
print("len(caches) = ", len(caches))

输出结果：

a[4][1] =  [-0.99999375  0.77911235 -0.99861469 -0.99833267]
a.shape =  (5, 10, 4)
y_pred[1][3] = [0.79560373 0.86224861 0.11118257 0.81515947]
y_pred.shape =  (2, 10, 4)
caches[1][1][3] = [-1.1425182  -0.34934272 -0.20889423  0.58662319]
len(caches) =  2

普通的RNN还可能存在梯度消失的问题，可以用LSTM（长短期忆）解决。

2.3 RNN的反向传播

基本上在各大框架中只需要实现前向传播就可以，框架会自动实现微积分前向传播的式子来实现反向传播，但是也可以自己代码实现一遍看一下他的实现过程也无妨，主要是求导公式比较复杂。

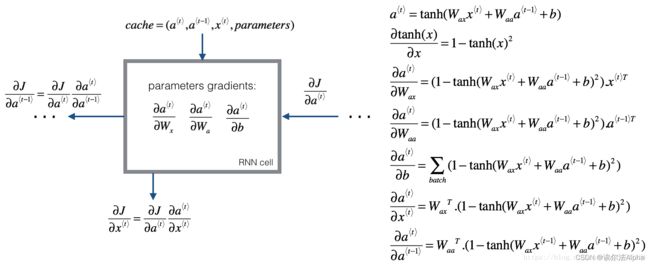
代价函数$J$(loss)的导数通过遵循链式规则从RNN进行反向传播，链式法则也用于计算$(\frac{\partial J}{\partial W_{ax}},\frac{\partial J}{\partial W_{aa}},\frac{\partial J}{\partial b})$来更新参数$(W_{ax},W_{aa})$。tanh(x)的导数是$1-\tanh (x{)}^2$，类似的，对于$(\frac{\partial J}{\partial W_{ax}},\frac{\partial J}{\partial W_{aa}},\frac{\partial J}{\partial b})$而言，$\tanh (u)$的导数是 $(1-\tanh (u{)}^2)du$。
首先构建一个单元的反向传播的实现：

def rnn_cell_backward(da_next, cache):
    """
    实现基本的RNN单元的单步反向传播

    参数：
        da_next -- 关于下一个隐藏状态的损失的梯度。
        cache -- 字典类型，rnn_step_forward()的输出

    返回：
        gradients -- 字典，包含了以下参数：
                        dx -- 输入数据的梯度，维度为(n_x, m)
                        da_prev -- 上一隐藏层的隐藏状态，维度为(n_a, m)
                        dWax -- 输入到隐藏状态的权重的梯度，维度为(n_a, n_x)
                        dWaa -- 隐藏状态到隐藏状态的权重的梯度，维度为(n_a, n_a)
                        dba -- 偏置向量的梯度，维度为(n_a, 1)
    """
    # 获取cache 的值
    a_next, a_prev, xt, parameters = cache

    # 从 parameters 中获取参数
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]

    # 计算tanh相对于a_next的梯度.
    dtanh = (1 - np.square(a_next)) * da_next

    # 计算关于Wax损失的梯度
    dxt = np.dot(Wax.T, dtanh)
    dWax = np.dot(dtanh, xt.T)

    # 计算关于Waa损失的梯度
    da_prev = np.dot(Waa.T, dtanh)
    dWaa = np.dot(dtanh, a_prev.T)

    # 计算关于b损失的梯度
    dba = np.sum(dtanh, keepdims=True, axis=-1)

    # 保存这些梯度到字典内
    gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba}

    return gradients

测试代码：

np.random.seed(1)
xt = np.random.randn(3, 10)
a_prev = np.random.randn(5, 10)
Wax = np.random.randn(5, 3)
Waa = np.random.randn(5, 5)
Wya = np.random.randn(2, 5)
ba = np.random.randn(5, 1)
by = np.random.randn(2, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}

a_next, yt, cache = rnn_cell_forward(xt, a_prev, parameters)

da_next = np.random.randn(5, 10)
gradients = rnn_cell_backward(da_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)

测试结果：

gradients["dxt"][1][2] = -1.3872130506020925
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = -0.15239949377395495
gradients["da_prev"].shape = (5, 10)
gradients["dWax"][3][1] = 0.4107728249354584
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = 1.1503450668497135
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [0.20023491]
gradients["dba"].shape = (5, 1)

接下来就实现整个RNN的反向传播：

def rnn_backward(da, caches):
    """
    在整个输入数据序列上实现RNN的反向传播

    参数：
        da -- 所有隐藏状态的梯度，维度为(n_a, m, T_x)
        caches -- 包含向前传播的信息的元组

    返回：
        gradients -- 包含了梯度的字典：
                        dx -- 关于输入数据的梯度，维度为(n_x, m, T_x)
                        da0 -- 关于初始化隐藏状态的梯度，维度为(n_a, m)
                        dWax -- 关于输入权重的梯度，维度为(n_a, n_x)
                        dWaa -- 关于隐藏状态的权值的梯度，维度为(n_a, n_a)
                        dba -- 关于偏置的梯度，维度为(n_a, 1)
    """
    # 从caches中获取第一个cache（t=1）的值
    caches, x = caches
    a1, a0, x1, parameters = caches[0]

    # 获取da与x1的维度信息
    n_a, m, T_x = da.shape
    n_x, m = x1.shape

    # 初始化梯度
    dx = np.zeros([n_x, m, T_x])
    dWax = np.zeros([n_a, n_x])
    dWaa = np.zeros([n_a, n_a])
    dba = np.zeros([n_a, 1])
    da0 = np.zeros([n_a, m])
    da_prevt = np.zeros([n_a, m])

    # 处理所有时间步
    for t in reversed(range(T_x)):
        # 计算时间步“t”时的梯度
        gradients = rnn_cell_backward(da[:, :, t] + da_prevt, caches[t])

        # 从梯度中获取导数
        dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients[
            "dWaa"], gradients["dba"]

        # 通过在时间步t添加它们的导数来增加关于全局导数的参数
        dx[:, :, t] = dxt
        dWax += dWaxt
        dWaa += dWaat
        dba += dbat

    # 将 da0设置为a的梯度，该梯度已通过所有时间步骤进行反向传播
    da0 = da_prevt

    # 保存这些梯度到字典内
    gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa, "dba": dba}

    return gradients

测试代码：

np.random.seed(1)
x = np.random.randn(3, 10, 4)
a0 = np.random.randn(5, 10)
Wax = np.random.randn(5, 3)
Waa = np.random.randn(5, 5)
Wya = np.random.randn(2, 5)
ba = np.random.randn(5, 1)
by = np.random.randn(2, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}
a, y, caches = rnn_forward(x, a0, parameters)
da = np.random.randn(5, 10, 4)
gradients = rnn_backward(da, caches)

print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWax\"].shape =", gradients["dWax"].shape)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWaa\"].shape =", gradients["dWaa"].shape)
print("gradients[\"dba\"][4] =", gradients["dba"][4])
print("gradients[\"dba\"].shape =", gradients["dba"].shape)

测试结果：

gradients["dx"][1][2] = [-2.07101689 -0.59255627  0.02466855  0.01483317]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.31494237512664996
gradients["da0"].shape = (5, 10)
gradients["dWax"][3][1] = 11.264104496527777
gradients["dWax"].shape = (5, 3)
gradients["dWaa"][1][2] = 2.303333126579893
gradients["dWaa"].shape = (5, 5)
gradients["dba"][4] = [-0.74747722]
gradients["dba"].shape = (5, 1)

3.LSTM

3.1 LSTM单元的构建

每个LSTM单元有长时间存储记忆的cell：$c^{⟨t⟩}$。

遗忘门：${\Gamma }_f^{⟨t⟩}=\sigma (W_f[a^{⟨t-1⟩},x^{⟨t⟩}]+b_f)$，由第4个公式$c^{⟨t⟩}$的计算式可得，当${\Gamma }_f^{⟨t⟩}$≈1时当前输出的记忆cell≈上一个记忆cell，即不更新。
更新门：${\Gamma }_u^{⟨t⟩}=\sigma (W_u[a^{⟨t-1⟩},x^{⟨t⟩}]+b_u)$，当${\Gamma }_u^{⟨t⟩}$≈1时当前输出的记忆cell被更新单元${\tilde{c}}^{⟨t⟩}$所代替，即作出更新。
最终输出的$c^{⟨t⟩}$由更新门和遗忘门作为权重（都为0～1）来决定的。
输出门：${\Gamma }_o^{⟨t⟩}=\sigma (W_o[a^{⟨t-1⟩},x^{⟨t⟩}]+b_o)$决定了输出的激活值，从而决定了输出的预测值。
把$a^{⟨t-1⟩},x^{⟨t⟩}$连接起来变为一个矩阵：$contact=\left[\begin{array}{c}{a}^{⟨t-1⟩}\\ x^{⟨t⟩}\end{array}\right]$

def lstm_cell_forward(xt, a_prev, c_prev, parameters):
    """
    根据图4实现一个LSTM单元的前向传播。

    参数：
        xt -- 在时间步“t”输入的数据，维度为(n_x, m)
        a_prev -- 上一个时间步“t-1”的隐藏状态，维度为(n_a, m)
        c_prev -- 上一个时间步“t-1”的记忆状态，维度为(n_a, m)
        parameters -- 字典类型的变量，包含了：
                        Wf -- 遗忘门的权值，维度为(n_a, n_a + n_x)
                        bf -- 遗忘门的偏置，维度为(n_a, 1)
                        Wi -- 更新门的权值，维度为(n_a, n_a + n_x)
                        bi -- 更新门的偏置，维度为(n_a, 1)
                        Wc -- 第一个“tanh”的权值，维度为(n_a, n_a + n_x)
                        bc -- 第一个“tanh”的偏置，维度为(n_a, n_a + n_x)
                        Wo -- 输出门的权值，维度为(n_a, n_a + n_x)
                        bo -- 输出门的偏置，维度为(n_a, 1)
                        Wy -- 隐藏状态与输出相关的权值，维度为(n_y, n_a)
                        by -- 隐藏状态与输出相关的偏置，维度为(n_y, 1)
    返回：
        a_next -- 下一个隐藏状态，维度为(n_a, m)
        c_next -- 下一个记忆状态，维度为(n_a, m)
        yt_pred -- 在时间步“t”的预测，维度为(n_y, m)
        cache -- 包含了反向传播所需要的参数，包含了(a_next, c_next, a_prev, c_prev, xt, parameters)

    注意：
        ft/it/ot表示遗忘/更新/输出门，cct表示候选值(c tilda)，c表示记忆值。
    """

    # 从“parameters”中获取相关值
    Wf = parameters["Wf"]
    bf = parameters["bf"]
    Wi = parameters["Wi"]
    bi = parameters["bi"]
    Wc = parameters["Wc"]
    bc = parameters["bc"]
    Wo = parameters["Wo"]
    bo = parameters["bo"]
    Wy = parameters["Wy"]
    by = parameters["by"]

    # 获取 xt 与 Wy 的维度信息
    n_x, m = xt.shape
    n_y, n_a = Wy.shape

    # 1.连接 a_prev 与 xt
    contact = np.zeros([n_a + n_x, m])
    # 将a和x赋值到contact
    contact[: n_a, :] = a_prev
    contact[n_a:, :] = xt

    # 2.根据公式计算ft、it、cct、c_next、ot、a_next
    ## 遗忘门，公式1
    ft = rnn_utils.sigmoid(np.dot(Wf, contact) + bf)

    ## 更新门，公式2
    it = rnn_utils.sigmoid(np.dot(Wi, contact) + bi)

    ## 更新单元，公式3
    cct = np.tanh(np.dot(Wc, contact) + bc)

    ## 最终的更新单元，公式4
    # c_next = np.multiply(ft, c_prev) + np.multiply(it, cct)
    c_next = ft * c_prev + it * cct
    ## 输出门，公式5
    ot = rnn_utils.sigmoid(np.dot(Wo, contact) + bo)

    ## 输出激活值，公式6
    # a_next = np.multiply(ot, np.tan(c_next))
    a_next = ot * np.tanh(c_next)

    # 3.计算LSTM单元的预测值
    yt_pred = rnn_utils.softmax(np.dot(Wy, a_next) + by)

    # 保存包含了反向传播所需要的参数
    cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters)

    return a_next, c_next, yt_pred, cache

测试代码正确性：

np.random.seed(1)
xt = np.random.randn(3, 10)
a_prev = np.random.randn(5, 10)
c_prev = np.random.randn(5, 10)
Wf = np.random.randn(5, 5 + 3)
bf = np.random.randn(5, 1)
Wi = np.random.randn(5, 5 + 3)
bi = np.random.randn(5, 1)
Wo = np.random.randn(5, 5 + 3)
bo = np.random.randn(5, 1)
Wc = np.random.randn(5, 5 + 3)
bc = np.random.randn(5, 1)
Wy = np.random.randn(2, 5)
by = np.random.randn(2, 1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)
print("a_next[4] = ", a_next[4])  # 取所有样本的随机一个激活值
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])  # 取所有样本的随机一个记忆状态值
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])  # 取所有样本的随机一个与预测值
print("yt.shape = ", yt.shape)
print("cache[1][3] =", cache[1][2])  # 取c_next[2]
print("len(cache) = ", len(cache))

这里的Wf、Wi、Wo、Wc等其实都是一个合并式子，如下图所示（以Wf来举例）：

Wf是Wfa和Wfx的横向叠加，所以Wf的维度在代码中是(5, 5 + 3)即($n_f$, $n_a$ + $n_x$)
测试结果：

a_next[4] =  [-0.66408471  0.0036921   0.02088357  0.22834167 -0.85575339  0.00138482
  0.76566531  0.34631421 -0.00215674  0.43827275]
a_next.shape =  (5, 10)
c_next[2] =  [ 0.63267805  1.00570849  0.35504474  0.20690913 -1.64566718  0.11832942
  0.76449811 -0.0981561  -0.74348425 -0.26810932]
c_next.shape =  (5, 10)
yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
 0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape =  (2, 10)
cache[1][3] = [ 0.63267805  1.00570849  0.35504474  0.20690913 -1.64566718  0.11832942
  0.76449811 -0.0981561  -0.74348425 -0.26810932]
len(cache) =  10

3.2 LSTM的前向传播

def lstm_forward(x, a0, parameters):
    """
    根据图5来实现LSTM单元组成的的循环神经网络

    参数：
        x -- 所有时间步的输入数据，维度为(n_x, m, T_x)
        a0 -- 初始化隐藏状态，维度为(n_a, m)
        parameters -- python字典，包含了以下参数：
                        Wf -- 遗忘门的权值，维度为(n_a, n_a + n_x)
                        bf -- 遗忘门的偏置，维度为(n_a, 1)
                        Wi -- 更新门的权值，维度为(n_a, n_a + n_x)
                        bi -- 更新门的偏置，维度为(n_a, 1)
                        Wc -- 第一个“tanh”的权值，维度为(n_a, n_a + n_x)
                        bc -- 第一个“tanh”的偏置，维度为(n_a, n_a + n_x)
                        Wo -- 输出门的权值，维度为(n_a, n_a + n_x)
                        bo -- 输出门的偏置，维度为(n_a, 1)
                        Wy -- 隐藏状态与输出相关的权值，维度为(n_y, n_a)
                        by -- 隐藏状态与输出相关的偏置，维度为(n_y, 1)

    返回：
        a -- 所有时间步的隐藏状态，维度为(n_a, m, T_x)
        y -- 所有时间步的预测值，维度为(n_y, m, T_x)
        caches -- 为反向传播的保存的元组，维度为（【列表类型】cache, x)）
    """

    # 初始化“caches”
    caches = []

    # 获取 xt 与 Wy 的维度信息
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wy"].shape

    # 使用0来初始化“a”、“c”、“y”
    a = np.zeros([n_a, m, T_x])
    c = np.zeros([n_a, m, T_x])
    y = np.zeros([n_y, m, T_x])

    # 初始化“a_next”、“c_next”
    a_next = a0
    c_next = np.zeros([n_a, m])

    # 遍历所有的时间步
    for t in range(T_x):
        # 更新下一个隐藏状态，下一个记忆状态，计算预测值，获取cache
        # a_next, c_next在=右边为a_t-1, c_t-1，在=左边为a_t, c_t
        a_next, c_next, yt_pred, cache = lstm_cell_forward(x[:, :, t], a_next, c_next, parameters)

        # 保存新的下一个隐藏状态到变量a中
        a[:, :, t] = a_next

        # 保存预测值到变量y中
        y[:, :, t] = yt_pred

        # 保存下一个单元状态到变量c中
        c[:, :, t] = c_next

        # 把cache添加到caches中
        caches.append(cache)

    # 保存反向传播需要的参数
    caches = (caches, x)

    return a, y, c, caches

测试代码：

np.random.seed(1)
x = np.random.randn(3, 10, 7)
a0 = np.random.randn(5, 10)
Wf = np.random.randn(5, 5 + 3)
bf = np.random.randn(5, 1)
Wi = np.random.randn(5, 5 + 3)
bi = np.random.randn(5, 1)
Wo = np.random.randn(5, 5 + 3)
bo = np.random.randn(5, 1)
Wc = np.random.randn(5, 5 + 3)
bc = np.random.randn(5, 1)
Wy = np.random.randn(2, 5)
by = np.random.randn(2, 1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a, y, c, caches = lstm_forward(x, a0, parameters)
print("a[4][3][6] = ", a[4][3][6])  # 取第7个时间步的第4个样本的第5个隐藏值
print("a.shape = ", a.shape)
print("y[1][4][3] =", y[1][4][3])  # 取第4个时间步的第5个样本的第2个预测值
print("y.shape = ", y.shape)
print("caches[1][1[1]] =", caches[1][1][1])  # 取caches中的输入值的所有时间步的第2个样本的第2个值
print("c[1][2][1]", c[1][2][1])  # 取第2个时间步的第3个样本的第2个记忆状态值
print("len(caches) = ", len(caches))

输出结果：

a[4][3][6] =  0.17211776753291672
a.shape =  (5, 10, 7)
y[1][4][3] = 0.9508734618501101
y.shape =  (2, 10, 7)
caches[1][1[1]] = [ 0.82797464  0.23009474  0.76201118 -0.22232814 -0.20075807  0.18656139
  0.41005165]
c[1][2][1] -0.8555449167181981
len(caches) =  2

3.3LSTM的反向传播

门的导数:
$$d{\Gamma }_o^{⟨t⟩}=d{a}_{next}\ast \tanh (c_{next})\ast {\Gamma }_o^{⟨t⟩}\ast (1-{\Gamma }_o^{⟨t⟩})\text{\hspace{1em}(1)}$$
$$d{\tilde{c}}^{⟨t⟩}=d{c}_{next}\ast {\Gamma }_i^{⟨t⟩}+{\Gamma }_o^{⟨t⟩}(1-\tanh (c_{next}{)}^2)\ast i_t\ast d{a}_{next}\ast {\tilde{c}}^{⟨t⟩}\ast (1-\tanh (\tilde{c}{)}^2)\text{\hspace{1em}(2)}$$
$$d{\Gamma }_u^{⟨t⟩}=d{c}_{next}\ast {\tilde{c}}^{⟨t⟩}+{\Gamma }_o^{⟨t⟩}(1-\tanh (c_{next}{)}^2)\ast {\tilde{c}}^{⟨t⟩}\ast d{a}_{next}\ast {\Gamma }_u^{⟨t⟩}\ast (1-{\Gamma }_u^{⟨t⟩})\text{\hspace{1em}(3)}$$
$$d{\Gamma }_f^{⟨t⟩}=d{c}_{next}\ast {\tilde{c}}_{prev}+{\Gamma }_o^{⟨t⟩}(1-\tanh (c_{next}{)}^2)\ast c_{prev}\ast d{a}_{next}\ast {\Gamma }_f^{⟨t⟩}\ast (1-{\Gamma }_f^{⟨t⟩})\text{\hspace{1em}(4)}$$
参数的导数:
$$d{W}_f=d{\Gamma }_f^{⟨t⟩}\ast {\left(\begin{array}{c}{a}_{prev}\\ x_t\end{array}\right)}^T\text{\hspace{1em}(5)}$$
$$d{W}_u=d{\Gamma }_u^{⟨t⟩}\ast {\left(\begin{array}{c}{a}_{prev}\\ x_t\end{array}\right)}^T\text{\hspace{1em}(6)}$$
$$d{W}_c=d{\tilde{c}}^{⟨t⟩}\ast {\left(\begin{array}{c}{a}_{prev}\\ x_t\end{array}\right)}^T\text{\hspace{1em}(7)}$$
$$d{W}_o=d{\Gamma }_o^{⟨t⟩}\ast {\left(\begin{array}{c}{a}_{prev}\\ x_t\end{array}\right)}^T\text{\hspace{1em}(8)}$$
为了计算$b_f,d{b}_u,d{b}_c,d{b}_o$我们需要在$d{\Gamma }_f^{⟨t⟩},d{\Gamma }_u^{⟨t⟩},d{\tilde{c}}^{⟨t⟩},d{\Gamma }_o^{⟨t⟩}$上使用(axis = 1)来进行求和，需要注意的事情是要使用keep_dims = True。
我们将计算关于先前隐藏状态、先前记忆状态和输入的导数。
$$d{a}_{prev}=W_f^T\ast d{\Gamma }_f^{⟨t⟩}+W_u^T\ast d{\Gamma }_u^{⟨t⟩}+W_c^T\ast d{\tilde{c}}^{⟨t⟩}+W_o^T\ast d{\Gamma }_o^{⟨t⟩}\text{\hspace{1em}(9)}$$
这里，方程13的权重是第一个 n_a, (比如$W_f=W_f[:n_a,:]$等等)

$$d{c}_{prev}=d{c}_{next}{\Gamma }_f^{⟨t⟩}+{\Gamma }_o^{⟨t⟩}\ast (1-\tanh (c_{next}{)}^2)\ast {\Gamma }_f^{⟨t⟩}\ast d{a}_{next}\text{\hspace{1em}(10)}$$

$$d{x}^{⟨t⟩}=W_f^T\ast d{\Gamma }_f^{⟨t⟩}+W_u^T\ast d{\Gamma }_u^{⟨t⟩}+W_c^T\ast d{\tilde{c}}_t+W_o^T\ast d{\Gamma }_o^{⟨t⟩}\text{\hspace{1em}(11)}$$
方程15的权值从n_a到结尾， (比如$W_f=W_f[n_a:,:]$等等)
首先实现单步的反向传播：

def lstm_cell_backward(da_next, dc_next, cache):
    """
    实现LSTM的单步反向传播

    参数：
        da_next -- 下一个隐藏状态的梯度，维度为(n_a, m)
        dc_next -- 下一个单元状态的梯度，维度为(n_a, m)
        cache -- 来自前向传播的一些参数

    返回：
        gradients -- 包含了梯度信息的字典：
                        dxt -- 输入数据的梯度，维度为(n_x, m)
                        da_prev -- 先前的隐藏状态的梯度，维度为(n_a, m)
                        dc_prev -- 前的记忆状态的梯度，维度为(n_a, m, T_x)
                        dWf -- 遗忘门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbf -- 遗忘门的偏置的梯度，维度为(n_a, 1)
                        dWi -- 更新门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbi -- 更新门的偏置的梯度，维度为(n_a, 1)
                        dWc -- 第一个“tanh”的权值的梯度，维度为(n_a, n_a + n_x)
                        dbc -- 第一个“tanh”的偏置的梯度，维度为(n_a, n_a + n_x)
                        dWo -- 输出门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbo -- 输出门的偏置的梯度，维度为(n_a, 1)
    """
    # 从cache中获取信息
    (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache

    # 获取xt与a_next的维度信息
    n_x, m = xt.shape
    n_a, m = a_next.shape

    # 根据公式1-4来计算门的导数
    dot = da_next * np.tanh(c_next) * ot * (1 - ot)
    dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
    dit = (dc_next * cct + ot * (1 - np.square(np.tanh(c_next))) * cct * da_next) * it * (1 - it)
    dft = (dc_next * c_prev + ot * (1 - np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1 - ft)

    # 根据公式5-8计算参数的导数
    concat = np.concatenate((a_prev, xt), axis=0).T
    dWf = np.dot(dft, concat)
    dWi = np.dot(dit, concat)
    dWc = np.dot(dcct, concat)
    dWo = np.dot(dot, concat)
    dbf = np.sum(dft, axis=1, keepdims=True)
    dbi = np.sum(dit, axis=1, keepdims=True)
    dbc = np.sum(dcct, axis=1, keepdims=True)
    dbo = np.sum(dot, axis=1, keepdims=True)

    # 使用公式9-11计算洗起来了隐藏状态、先前记忆状态、输入的导数。
    da_prev = np.dot(parameters["Wf"][:, :n_a].T, dft) + np.dot(parameters["Wc"][:, :n_a].T, dcct) + np.dot(
        parameters["Wi"][:, :n_a].T, dit) + np.dot(parameters["Wo"][:, :n_a].T, dot)

    dc_prev = dc_next * ft + ot * (1 - np.square(np.tanh(c_next))) * ft * da_next

    dxt = np.dot(parameters["Wf"][:, n_a:].T, dft) + np.dot(parameters["Wc"][:, n_a:].T, dcct) + np.dot(
        parameters["Wi"][:, n_a:].T, dit) + np.dot(parameters["Wo"][:, n_a:].T, dot)

    # 保存梯度信息到字典
    gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf, "dbf": dbf, "dWi": dWi, "dbi": dbi,
                 "dWc": dWc, "dbc": dbc, "dWo": dWo, "dbo": dbo}

    return gradients

测试代码：

np.random.seed(1)
xt = np.random.randn(3, 10)
a_prev = np.random.randn(5, 10)
c_prev = np.random.randn(5, 10)
Wf = np.random.randn(5, 5 + 3)
bf = np.random.randn(5, 1)
Wi = np.random.randn(5, 5 + 3)
bi = np.random.randn(5, 1)
Wo = np.random.randn(5, 5 + 3)
bo = np.random.randn(5, 1)
Wc = np.random.randn(5, 5 + 3)
bc = np.random.randn(5, 1)
Wy = np.random.randn(2, 5)
by = np.random.randn(2, 1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a_next, c_next, yt, cache = lstm_cell_forward(xt, a_prev, c_prev, parameters)

da_next = np.random.randn(5, 10)
dc_next = np.random.randn(5, 10)
gradients = lstm_cell_backward(da_next, dc_next, cache)
print("gradients[\"dxt\"][1][2] =", gradients["dxt"][1][2])
print("gradients[\"dxt\"].shape =", gradients["dxt"].shape)
print("gradients[\"da_prev\"][2][3] =", gradients["da_prev"][2][3])
print("gradients[\"da_prev\"].shape =", gradients["da_prev"].shape)
print("gradients[\"dc_prev\"][2][3] =", gradients["dc_prev"][2][3])
print("gradients[\"dc_prev\"].shape =", gradients["dc_prev"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)

测试结果：

gradients["dxt"][1][2] = 3.2305591151091884
gradients["dxt"].shape = (3, 10)
gradients["da_prev"][2][3] = -0.06396214197109241
gradients["da_prev"].shape = (5, 10)
gradients["dc_prev"][2][3] = 0.7975220387970015
gradients["dc_prev"].shape = (5, 10)
gradients["dWf"][3][1] = -0.1479548381644968
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = 1.0574980552259903
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = 2.3045621636876676
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = 0.3313115952892109
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [0.18864637]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.40142491]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [0.25587763]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [0.13893342]
gradients["dbo"].shape = (5, 1)

接下来进行LSTM网络的反向传播：

def lstm_backward(da, caches):
    """
    实现LSTM网络的反向传播

    参数：
        da -- 关于隐藏状态的梯度，维度为(n_a, m, T_x)
        cachses -- 前向传播保存的信息

    返回：
        gradients -- 包含了梯度信息的字典：
                        dx -- 输入数据的梯度，维度为(n_x, m，T_x)
                        da0 -- 先前的隐藏状态的梯度，维度为(n_a, m)
                        dWf -- 遗忘门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbf -- 遗忘门的偏置的梯度，维度为(n_a, 1)
                        dWi -- 更新门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbi -- 更新门的偏置的梯度，维度为(n_a, 1)
                        dWc -- 第一个“tanh”的权值的梯度，维度为(n_a, n_a + n_x)
                        dbc -- 第一个“tanh”的偏置的梯度，维度为(n_a, n_a + n_x)
                        dWo -- 输出门的权值的梯度，维度为(n_a, n_a + n_x)
                        dbo -- 输出门的偏置的梯度，维度为(n_a, 1)

    """

    # 从caches中获取第一个cache（t=1）的值
    caches, x = caches
    (a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0]

    # 获取da与x1的维度信息
    n_a, m, T_x = da.shape
    n_x, m = x1.shape

    # 初始化梯度
    dx = np.zeros([n_x, m, T_x])
    da0 = np.zeros([n_a, m])
    da_prevt = np.zeros([n_a, m])
    dc_prevt = np.zeros([n_a, m])
    dWf = np.zeros([n_a, n_a + n_x])
    dWi = np.zeros([n_a, n_a + n_x])
    dWc = np.zeros([n_a, n_a + n_x])
    dWo = np.zeros([n_a, n_a + n_x])
    dbf = np.zeros([n_a, 1])
    dbi = np.zeros([n_a, 1])
    dbc = np.zeros([n_a, 1])
    dbo = np.zeros([n_a, 1])

    # 处理所有时间步
    for t in reversed(range(T_x)):
        # 使用lstm_cell_backward函数计算所有梯度
        gradients = lstm_cell_backward(da[:, :, t], dc_prevt, caches[t])
        # 保存相关参数
        dx[:, :, t] = gradients['dxt']
        dWf = dWf + gradients['dWf']
        dWi = dWi + gradients['dWi']
        dWc = dWc + gradients['dWc']
        dWo = dWo + gradients['dWo']
        dbf = dbf + gradients['dbf']
        dbi = dbi + gradients['dbi']
        dbc = dbc + gradients['dbc']
        dbo = dbo + gradients['dbo']
    # 将第一个激活的梯度设置为反向传播的梯度da_prev。
    da0 = gradients['da_prev']

    # 保存所有梯度到字典变量内
    gradients = {"dx": dx, "da0": da0, "dWf": dWf, "dbf": dbf, "dWi": dWi, "dbi": dbi,
                 "dWc": dWc, "dbc": dbc, "dWo": dWo, "dbo": dbo}

    return gradients

测试代码：

np.random.seed(1)
x = np.random.randn(3, 10, 7)
a0 = np.random.randn(5, 10)
Wf = np.random.randn(5, 5 + 3)
bf = np.random.randn(5, 1)
Wi = np.random.randn(5, 5 + 3)
bi = np.random.randn(5, 1)
Wo = np.random.randn(5, 5 + 3)
bo = np.random.randn(5, 1)
Wc = np.random.randn(5, 5 + 3)
bc = np.random.randn(5, 1)
Wy = np.random.randn(2, 5)
by = np.random.randn(2, 1)

parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}

a, y, c, caches = lstm_forward(x, a0, parameters)

da = np.random.randn(5, 10, 4)
gradients = lstm_backward(da, caches)

print("gradients[\"dx\"][1][2] =", gradients["dx"][1][2])
print("gradients[\"dx\"].shape =", gradients["dx"].shape)
print("gradients[\"da0\"][2][3] =", gradients["da0"][2][3])
print("gradients[\"da0\"].shape =", gradients["da0"].shape)
print("gradients[\"dWf\"][3][1] =", gradients["dWf"][3][1])
print("gradients[\"dWf\"].shape =", gradients["dWf"].shape)
print("gradients[\"dWi\"][1][2] =", gradients["dWi"][1][2])
print("gradients[\"dWi\"].shape =", gradients["dWi"].shape)
print("gradients[\"dWc\"][3][1] =", gradients["dWc"][3][1])
print("gradients[\"dWc\"].shape =", gradients["dWc"].shape)
print("gradients[\"dWo\"][1][2] =", gradients["dWo"][1][2])
print("gradients[\"dWo\"].shape =", gradients["dWo"].shape)
print("gradients[\"dbf\"][4] =", gradients["dbf"][4])
print("gradients[\"dbf\"].shape =", gradients["dbf"].shape)
print("gradients[\"dbi\"][4] =", gradients["dbi"][4])
print("gradients[\"dbi\"].shape =", gradients["dbi"].shape)
print("gradients[\"dbc\"][4] =", gradients["dbc"][4])
print("gradients[\"dbc\"].shape =", gradients["dbc"].shape)
print("gradients[\"dbo\"][4] =", gradients["dbo"][4])
print("gradients[\"dbo\"].shape =", gradients["dbo"].shape)

测试结果：

gradients["dx"][1][2] = [ 0.01980463 -0.02745056 -0.31327706  0.53886581]
gradients["dx"].shape = (3, 10, 4)
gradients["da0"][2][3] = -0.0002844952897491093
gradients["da0"].shape = (5, 10)
gradients["dWf"][3][1] = -0.015389004332725812
gradients["dWf"].shape = (5, 8)
gradients["dWi"][1][2] = -0.10924217935041784
gradients["dWi"].shape = (5, 8)
gradients["dWc"][3][1] = 0.07939058449325513
gradients["dWc"].shape = (5, 8)
gradients["dWo"][1][2] = -0.08101445436214824
gradients["dWo"].shape = (5, 8)
gradients["dbf"][4] = [-0.24148921]
gradients["dbf"].shape = (5, 1)
gradients["dbi"][4] = [-0.08824333]
gradients["dbi"].shape = (5, 1)
gradients["dbc"][4] = [0.14411048]
gradients["dbc"].shape = (5, 1)
gradients["dbo"][4] = [-0.45977321]
gradients["dbo"].shape = (5, 1)

4.应用

导入所需包cllm_utils.py：

import numpy as np


def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum(axis=0)


def smooth(loss, cur_loss):
    return loss * 0.999 + cur_loss * 0.001


def print_sample(sample_ix, ix_to_char):
    txt = ''.join(ix_to_char[ix] for ix in sample_ix)
    txt = txt[0].upper() + txt[1:]  # capitalize first character 
    print('%s' % (txt,), end='')


def get_initial_loss(vocab_size, seq_length):
    return -np.log(1.0 / vocab_size) * seq_length


def softmax(x):
    e_x = np.exp(x - np.max(x))
    return e_x / e_x.sum(axis=0)


def initialize_parameters(n_a, n_x, n_y):
    """
    Initialize parameters with small random values
    
    Returns:
    parameters -- python dictionary containing:
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        b --  Bias, numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
    """
    np.random.seed(1)
    Wax = np.random.randn(n_a, n_x) * 0.01  # input to hidden
    Waa = np.random.randn(n_a, n_a) * 0.01  # hidden to hidden
    Wya = np.random.randn(n_y, n_a) * 0.01  # hidden to output
    b = np.zeros((n_a, 1))  # hidden bias
    by = np.zeros((n_y, 1))  # output bias

    parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}

    return parameters


def rnn_step_forward(parameters, a_prev, x):
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    a_next = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + b)  # hidden state
    p_t = softmax(
        np.dot(Wya, a_next) + by)  # unnormalized log probabilities for next chars # probabilities for next chars 

    return a_next, p_t


def rnn_step_backward(dy, gradients, parameters, x, a, a_prev):
    gradients['dWya'] += np.dot(dy, a.T)
    gradients['dby'] += dy
    da = np.dot(parameters['Wya'].T, dy) + gradients['da_next']  # backprop into h
    daraw = (1 - a * a) * da  # backprop through tanh nonlinearity
    gradients['db'] += daraw
    gradients['dWax'] += np.dot(daraw, x.T)
    gradients['dWaa'] += np.dot(daraw, a_prev.T)
    gradients['da_next'] = np.dot(parameters['Waa'].T, daraw)
    return gradients


def update_parameters(parameters, gradients, lr):
    parameters['Wax'] += -lr * gradients['dWax']
    parameters['Waa'] += -lr * gradients['dWaa']
    parameters['Wya'] += -lr * gradients['dWya']
    parameters['b'] += -lr * gradients['db']
    parameters['by'] += -lr * gradients['dby']
    return parameters


def rnn_forward(X, Y, a0, parameters, vocab_size=27):
    # Initialize x, a and y_hat as empty dictionaries
    x, a, y_hat = {}, {}, {}

    a[-1] = np.copy(a0)

    # initialize your loss to 0
    loss = 0

    for t in range(len(X)):

        # Set x[t] to be the one-hot vector representation of the t'th character in X.
        # if X[t] == None, we just have x[t]=0. This is used to set the input for the first timestep to the zero vector. 
        x[t] = np.zeros((vocab_size, 1))
        if (X[t] != None):
            x[t][X[t]] = 1

        # Run one step forward of the RNN
        a[t], y_hat[t] = rnn_step_forward(parameters, a[t - 1], x[t])

        # Update the loss by substracting the cross-entropy term of this time-step from it.
        loss -= np.log(y_hat[t][Y[t], 0])

    cache = (y_hat, a, x)

    return loss, cache


def rnn_backward(X, Y, parameters, cache):
    # Initialize gradients as an empty dictionary
    gradients = {}

    # Retrieve from cache and parameters
    (y_hat, a, x) = cache
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']

    # each one should be initialized to zeros of the same dimension as its corresponding parameter
    gradients['dWax'], gradients['dWaa'], gradients['dWya'] = np.zeros_like(Wax), np.zeros_like(Waa), np.zeros_like(Wya)
    gradients['db'], gradients['dby'] = np.zeros_like(b), np.zeros_like(by)
    gradients['da_next'] = np.zeros_like(a[0])

    ### START CODE HERE ###
    # Backpropagate through time
    for t in reversed(range(len(X))):
        dy = np.copy(y_hat[t])
        dy[Y[t]] -= 1
        gradients = rnn_step_backward(dy, gradients, parameters, x[t], a[t], a[t - 1])
    ### END CODE HERE ###

    return gradients, a

4.1字符级语言模型 - 恐龙岛

通过收集到的恐龙名字，并编入了这个数据集，通过构建字符级语言模型来随机生成新的名称。

首先进行处理数据

首先将数据集放在工程内。
读书数据集，查看其数据量：

# 获取名称
data = ""
with open("dinos.txt", "r") as f1:
    data = f1.read()

# 转化为小写字符
data = data.lower()

# 转化为无序且不重复的元素列表
chars = list(set(data))

# 获取大小信息
data_size, vocab_size = len(data), len(chars)

print(chars)
print("共计有%d个字符，唯一字符有%d个" % (data_size, vocab_size))

运行结果：

['d', 'v', 'e', 'x', 'k', 'a', 'r', 'p', 'q', 's', 'w', 'b', 'z', 'f', 'm', 'n', 'c', 'g', 'l', 'u', 'h', 't', 'y', 'j', 'o', '\n', 'i']
共计有19909个字符，唯一字符有27个

这些字符是a-z（26个英文字符）加上“\n”（换行字符），在这里换行字符相当于（句子结束符）的作用，但在这里不是句子还是名字所以表示了名字的结束而不是句子的结尾。下面将创建一个字典，每个字符映射到0-26的索引，然后再创建一个字典，它将该字典将每个索引映射回相应的字符，在softmax层的概率分布时可以找到并输出相应的字符。

char_to_ix = {ch: i for i, ch in enumerate(sorted(chars))}
ix_to_char = {i: ch for i, ch in enumerate(sorted(chars))}

print(char_to_ix)
print(ix_to_char)

运行结果：

{'\n': 0, 'a': 1, 'b': 2, 'c': 3, 'd': 4, 'e': 5, 'f': 6, 'g': 7, 'h': 8, 'i': 9, 'j': 10, 'k': 11, 'l': 12, 'm': 13, 'n': 14, 'o': 15, 'p': 16, 'q': 17, 'r': 18, 's': 19, 't': 20, 'u': 21, 'v': 22, 'w': 23, 'x': 24, 'y': 25, 'z': 26}
{0: '\n', 1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z'}

构建模型

使用普通的RNN，构建顺序如下：
初始化参数 —> 循环迭代[前向传播计算loss、反向传播计算梯度、修剪梯度以免梯度爆炸、用梯度下降更新规则更新参数] —> 得到最终学习到的参数

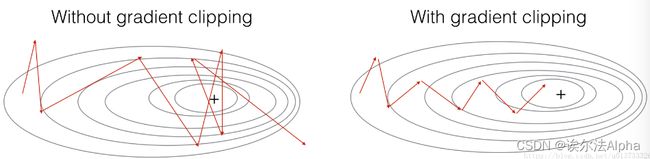
• 梯度修剪：避免梯度爆炸
• 取样:一种用来产生字符的技术

梯度修剪

为了避免梯度爆炸的现象本篇将使用较为简单的梯度修剪的方法，简单来说梯度向量的每一个元素都被限制在[− N ，N ]的范围，比如有一个maxValue（比如10），如果梯度的任何值大于10，那么它将被设置为10，如果梯度的任何值小于-10，那么它将被设置为-10，如果它在-10与10之间，那么它将不变。

def clip(gradients, maxValue):
    """
    使用maxValue来修剪梯度

    参数：
        gradients -- 字典类型，包含了以下参数："dWaa", "dWax", "dWya", "db", "dby"
        maxValue -- 阈值，把梯度值限制在[-maxValue, maxValue]内

    返回：
        gradients -- 修剪后的梯度
    """
    # 获取参数
    dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients[
        'dby']

    # 梯度修剪
    for gradient in [dWaa, dWax, dWya, db, dby]:
        np.clip(gradient, -maxValue, maxValue, out=gradient)

    gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}

    return gradients

测试代码：

np.random.seed(3)
dWax = np.random.randn(5, 3) * 10
dWaa = np.random.randn(5, 5) * 10
dWya = np.random.randn(2, 5) * 10
db = np.random.randn(5, 1) * 10
dby = np.random.randn(2, 1) * 10
gradients = {"dWax": dWax, "dWaa": dWaa, "dWya": dWya, "db": db, "dby": dby}
gradients = clip(gradients, 10)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("gradients[\"dWax\"][3][1] =", gradients["dWax"][3][1])
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])

运行结果：

gradients["dWaa"][1][2] = 10.0
gradients["dWax"][3][1] = -10.0
gradients["dWya"][1][2] = 0.2971381536101662
gradients["db"][4] = [10.]
gradients["dby"][1] = [8.45833407]

采样

现在假设我们的模型已经训练过了，我们希望生成新的文本，生成的过程如下图：

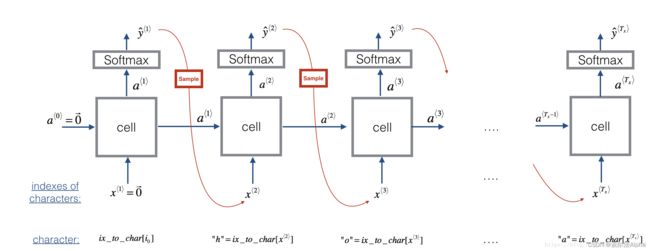
在这幅图中，我们假设模型已经经过了训练。我们在第一步传入$x^{⟨1⟩}=0$，然后让网络一次对一个字符进行采样。
通过以下4步构建图中的sample函数：

• 步骤1：网络的第一个“伪”输入$x^{⟨1⟩}=0$（零向量），这是在生成字符之前的默认输入，同时我们设置$a^{⟨0⟩}=0$
• 步骤2：运行一次（一个时间步）前向传播，然后得到$a^{⟨1⟩}$与${\hat{y}}^{⟨1⟩}$，公式如下:

$$a^{⟨t+1⟩}=\tanh (W_{ax}{x}^{⟨t+1⟩}+W_{aa}{a}^{⟨t⟩}+b)\text{\hspace{1em}(1)}$$
$$z^{⟨t+1⟩}=W_{ya}{a}^{⟨t+1⟩}+b_y\text{\hspace{1em}(2)}$$
$${\hat{y}}^{⟨t+1⟩}=softmax(z^{⟨t+1⟩})\text{\hspace{1em}(3)}$$
需要注意的是${\hat{y}}^{⟨t+1⟩}$是一个softmax概率向量（其下的值在0到1之间，总和为1），${\hat{y}}_i^{⟨t+1⟩}$表示索引“i”的字符是下一个字符的概率。

• 步骤3：采样：根据${\hat{y}}^{⟨t+1⟩}$指定的概率分布选择下一个字符的索引，假如${\hat{y}}_i^{⟨t+1⟩}=0.16$，那么选择索引“i”的概率为16%，为了实现它，我们可以使用np.random.choice函数：

np.random.seed(0)
p = np.array([0.1, 0.0, 0.7, 0.2])
index = np.random.choice([0, 1, 2, 3], p = p.ravel())

这意味着你将根据分布选择索引：
$P(index=0)=0.1,P(index=1)=0.0,P(index=2)=0.7,P(index=3)=0.2$，这代表索引为2的概率最高最容易被抽取。

• 步骤4：在sample()中实现的最后一步是用$x^{⟨t+1⟩}$的值覆盖变量x(当前存储$x^{⟨t⟩}$)。我们将通过创建一个与我们所选择的字符相对应的一个one-hot向量来表示$x^{⟨t+1⟩}$。然后在步骤1中向前传播$x^{⟨t+1⟩}$，并不断重复这个过程，直到得到一个“\n”字符，表明已经到达恐龙名称的末尾。

def sample(parameters, char_to_ix, seed):
    """
    根据RNN输出的概率分布序列对字符序列进行采样

    参数：
        parameters -- 包含了Waa, Wax, Wya, by, b的字典
        char_to_ix -- 字符映射到索引的字典
        seed -- 随机种子

    返回：
        indices -- 包含采样字符索引的长度为n的列表。
    """

    # 从parameters 中获取参数
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    vocab_size = by.shape[0]
    n_a = Waa.shape[1]

    # 步骤1
    ## 创建one-hot向量x
    x = np.zeros((vocab_size, 1))

    ## 使用0初始化a_prev
    a_prev = np.zeros((n_a, 1))

    # 创建索引的空列表，这是包含要生成的字符的索引的列表。
    indices = []

    # idx是检测换行符的标志，我们将其初始化为-1。
    idx = -1

    # 循环遍历时间步骤t。在每个时间步中，从概率分布中抽取一个字符，
    # 并将其索引附加到“indices”上，如果达到50个字符（尽管几乎不可能会有50个字符的名字）将停止循环，防止进入无限循环
    counter = 0
    newline_character = char_to_ix["\n"]

    while (idx != newline_character and counter < 50):
        # 步骤2：使用公式1、2、3进行前向传播
        a = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + b)
        z = np.dot(Wya, a) + by
        y = cllm_utils.softmax(z)

        # 设定随机种子
        np.random.seed(counter + seed)

        # 步骤3：从概率分布y中抽取词汇表中字符的索引
        idx = np.random.choice(list(range(vocab_size)), p=y.ravel())

        # 添加到索引中
        indices.append(idx)

        # 步骤4:将输入字符重写为与采样索引对应的字符。
        x = np.zeros((vocab_size, 1))
        x[idx] = 1

        # 更新a_prev为a
        a_prev = a

        # 累加器
        seed += 1
        counter += 1

    if (counter == 50):
        indices.append(char_to_ix["\n"])

    return indices

测试代码：

np.random.seed(2)
_, n_a = 20, 100
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}

indices = sample(parameters, char_to_ix, 0)
print("Sampling:")
print("list of sampled indices:", indices)
print("list of sampled characters:", [ix_to_char[i] for i in indices])

测试结果：

Sampling:
list of sampled indices: [12, 17, 24, 14, 13, 9, 10, 22, 24, 6, 13, 11, 12, 6, 21, 15, 21, 14, 3, 2, 1, 21, 18, 24, 7, 25, 6, 25, 18, 10, 16, 2, 3, 8, 15, 12, 11, 7, 1, 12, 10, 2, 7, 7, 11, 17, 24, 12, 13, 24, 0]
list of sampled characters: ['l', 'q', 'x', 'n', 'm', 'i', 'j', 'v', 'x', 'f', 'm', 'k', 'l', 'f', 'u', 'o', 'u', 'n', 'c', 'b', 'a', 'u', 'r', 'x', 'g', 'y', 'f', 'y', 'r', 'j', 'p', 'b', 'c', 'h', 'o', 'l', 'k', 'g', 'a', 'l', 'j', 'b', 'g', 'g', 'k', 'q', 'x', 'l', 'm', 'x', '\n']

构建语言模型

梯度下降

一次训练一个样本，所以优化算法将是随机梯度下降，以下是RNN的一个通用的优化循环的步骤：

• 前向传播计算损失
• 反向传播计算关于参数的梯度损失
• 修剪梯度
• 使用梯度下降更新参数
  构建优化函数：

def optimize(X, Y, a_prev, parameters, learning_rate=0.01):
    """
    执行训练模型的单步优化。

    参数：
        X -- 整数列表，其中每个整数映射到词汇表中的字符。
        Y -- 整数列表，与X完全相同，但向左移动了一个索引。
        a_prev -- 上一个隐藏状态
        parameters -- 字典，包含了以下参数：
                        Wax -- 权重矩阵乘以输入，维度为(n_a, n_x)
                        Waa -- 权重矩阵乘以隐藏状态，维度为(n_a, n_a)
                        Wya -- 隐藏状态与输出相关的权重矩阵，维度为(n_y, n_a)
                        b -- 偏置，维度为(n_a, 1)
                        by -- 隐藏状态与输出相关的权重偏置，维度为(n_y, 1)
        learning_rate -- 模型学习的速率

    返回：
        loss -- 损失函数的值（交叉熵损失CE）
        gradients -- 字典，包含了以下参数：
                        dWax -- 输入到隐藏的权值的梯度，维度为(n_a, n_x)
                        dWaa -- 隐藏到隐藏的权值的梯度，维度为(n_a, n_a)
                        dWya -- 隐藏到输出的权值的梯度，维度为(n_y, n_a)
                        db -- 偏置的梯度，维度为(n_a, 1)
                        dby -- 输出偏置向量的梯度，维度为(n_y, 1)
        a[len(X)-1] -- 最后的隐藏状态，维度为(n_a, 1)
    """

    # 前向传播
    loss, cache = cllm_utils.rnn_forward(X, Y, a_prev, parameters)

    # 反向传播
    gradients, a = cllm_utils.rnn_backward(X, Y, parameters, cache)

    # 梯度修剪，[-5 , 5]
    gradients = clip(gradients, 5)

    # 更新参数
    parameters = cllm_utils.update_parameters(parameters, gradients, learning_rate)

    return loss, gradients, a[len(X) - 1]

测试代码：

np.random.seed(1)
vocab_size, n_a = 27, 100
a_prev = np.random.randn(n_a, 1)
Wax, Waa, Wya = np.random.randn(n_a, vocab_size), np.random.randn(n_a, n_a), np.random.randn(vocab_size, n_a)
b, by = np.random.randn(n_a, 1), np.random.randn(vocab_size, 1)
parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "b": b, "by": by}
X = [12, 3, 5, 11, 22, 3]
Y = [4, 14, 11, 22, 25, 26]

loss, gradients, a_last = optimize(X, Y, a_prev, parameters, learning_rate=0.01)
print("Loss =", loss)
print("gradients[\"dWaa\"][1][2] =", gradients["dWaa"][1][2])
print("np.argmax(gradients[\"dWax\"]) =", np.argmax(gradients["dWax"]))
print("gradients[\"dWya\"][1][2] =", gradients["dWya"][1][2])
print("gradients[\"db\"][4] =", gradients["db"][4])
print("gradients[\"dby\"][1] =", gradients["dby"][1])
print("a_last[4] =", a_last[4])

运行结果：

Loss = 126.50397572165335
gradients["dWaa"][1][2] = 0.1947093153472637
np.argmax(gradients["dWax"]) = 93
gradients["dWya"][1][2] = -0.007773876032004358
gradients["db"][4] = [-0.06809825]
gradients["dby"][1] = [0.01538192]
a_last[4] = [-1.]

训练模型

def model(data, ix_to_char, char_to_ix, num_iterations=3500,
          n_a=50, dino_names=7, vocab_size=27):
    """
    训练模型并生成恐龙名字

    参数：
        data -- 语料库
        ix_to_char -- 索引映射字符字典
        char_to_ix -- 字符映射索引字典
        num_iterations -- 迭代次数
        n_a -- RNN单元数量
        dino_names -- 每次迭代中采样的数量
        vocab_size -- 在文本中的唯一字符的数量

    返回：
        parameters -- 学习后了的参数
    """

    # 从vocab_size中获取n_x、n_y
    n_x, n_y = vocab_size, vocab_size

    # 初始化参数
    parameters = cllm_utils.initialize_parameters(n_a, n_x, n_y)

    # 初始化损失
    loss = cllm_utils.get_initial_loss(vocab_size, dino_names)

    # 构建恐龙名称列表
    with open("dinos.txt") as f:
        examples = f.readlines()
    examples = [x.lower().strip() for x in examples]

    # 打乱全部的恐龙名称
    np.random.seed(0)
    np.random.shuffle(examples)

    # 初始化LSTM隐藏状态
    a_prev = np.zeros((n_a, 1))

    # 循环
    for j in range(num_iterations):
        # 定义一个训练样本
        index = j % len(examples)
        X = [None] + [char_to_ix[ch] for ch in examples[index]]    # 解释为0向量
        Y = X[1:] + [char_to_ix["\n"]]

        # 执行单步优化：前向传播 -> 反向传播 -> 梯度修剪 -> 更新参数
        # 选择学习率为0.01
        curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters)

        # 使用延迟来保持损失平滑,这是为了加速训练。
        loss = cllm_utils.smooth(loss, curr_loss)

        # 每2000次迭代，通过sample()生成“\n”字符，检查模型是否学习正确
        if j % 2000 == 0:
            print("第" + str(j + 1) + "次迭代，损失值为：" + str(loss))

            seed = 0
            for name in range(dino_names):
                # 采样
                sampled_indices = sample(parameters, char_to_ix, seed)
                cllm_utils.print_sample(sampled_indices, ix_to_char)

                # 为了得到相同的效果，随机种子+1
                seed += 1

            print("\n")
    return parameters

测试：

#开始时间
start_time = time.clock()

#开始训练
parameters = model(data, ix_to_char, char_to_ix, num_iterations=3500)

#结束时间
end_time = time.clock()

#计算时差
minium = end_time - start_time

print("执行了：" + str(int(minium / 60)) + "分" + str(int(minium%60)) + "秒")

运行结果：

第1次迭代，损失值为：23.087336085484605
Nkzxwtdmfqoeyhsqwasjkjvu
Kneb
Kzxwtdmfqoeyhsqwasjkjvu
Neb
Zxwtdmfqoeyhsqwasjkjvu
Eb
Xwtdmfqoeyhsqwasjkjvu


第2001次迭代，损失值为：27.884160491415773
Liusskeomnolxeros
Hmdaairus
Hytroligoraurus
Lecalosapaus
Xusicikoraurus
Abalpsamantisaurus
Tpraneronxeros

待更新…