中国大学MOOC-陈越、何钦铭-数据结构-习题解答-02 线性结构

1. 02-线性结构1 两个有序链表序列的合并 (15 分)

【题目描述】

题目链接

【题解】

本题的一个关键是搞清楚带头结点的链表和不带头结点的链表到底有什么区别和联系，如果没注意到这一点，那么输出会不正确，得一直调整输出。

• 带头结点的链表有一个头结点，这个头结点的数据域是空的，指针域指向链表的存有数据的第一个结点（也就是整个链表的第二个结点）。头结点相当于整个链表的入口；
• 不带头结点的链表的第一个结点就是链表存有数据的第一个结点；
• 无论链表带不带头结点，链表的头指针都指向整个链表的第一个结点。

/*本题有个点不容易发现，就是他强调链表带有头结点，如果考虑不到这一点就得不到正确的输出*/
List Merge( List L1, List L2 )
{
    List p1=L1->Next,p2=L2->Next,L,L_start;    //p1和p2指向头结点的下一个结点（存有数据的第一个结点）
    L=(List)malloc(sizeof(List));              //先创建一个头结点
    L->Next=NULL;
    L_start=L;                                 //头指针指向头结点
    while (p1 && p2) {
        if (p1->Data<=p2->Data) {
            L->Next=p1;
            L=L->Next;                         //L和p均需要移位
            p1=p1->Next;
        } else {
            L->Next=p2;
            L=L->Next;
            p2=p2->Next;
        }
    }
    if (p1)              //直接让L连接上非空的链表的后续部分就行了，无需循环移位操作
        L->Next=p1; 
    else if (p2) 
        L->Next=p2;
    L1->Next=NULL;       //让L1和L2只有头结点，其余的数据结点全部断开
    L2->Next=NULL;
    
    return L_start;
}

2. 02-线性结构2 一元多项式的乘法与加法运算 (20 分)

【题目描述】

题目链接

【题解】

这个题写代码+debug花了我近5个小时。。。主要是debug的时间太长（差不多占了一半以上的时间），关键原因就是题目的描述和要求没有理解透，血的教训啊！！！

该题的解决要点如下：

• 零多项式与常数多项式：做这个题目要区分清楚“零多项式”与“常数多项式”的具体含义和输出格式分别是什么，不然你没法通过最后一个测点。所谓零多项式，指的是所有项（包括常数项）的系数均为0，而常数多项式则是常数项系数不为0，其他项系数均为0；
• 输入格式上：题目保证先给出非零项的个数（很重要，如果输入零多项式，那么输入格式为“0”），如果有非零项，则按照降幂顺序输入（有序输入，加法结果无需再排序）；
• 输出格式上：零多项式输出为“0 0”，其他项则只输出非零项；
• 本题要采用结构化设计，将功能的实现分解为多项式读入、多项式输出、加法、乘法等四个函数，另外需要一个辅助函数——插入函数；
• 具体函数的代码书写上，要运用已经学过的线性表这一抽像数据类型，通过它的基本操作来编写代码，物理存储上用链表实现；
• 乘法的实现需要考虑合并同类项和降幂输出，通过线性表的插入操作来实现；
• 多项式输出函数的设计要注意，如何去处理空格、如何处理零多项式和空链表等等，具体见代码注释。

#include 
#include 
#include 
#define ElementType int
typedef struct PolyNodes* List;                 /*多项式结点的定义*/
struct PolyNodes {
    ElementType coef;
    ElementType expon;
    List next;
};
List input(int n);                              //多项式输入函数
void output(List const L);                      //多项式输出函数
List multiply(List const L1, List const L2);    //多项式乘法函数
List plus(List const L1, List const L2);        //多项式加法函数
List insert(List L, List X);                    //辅助函数：结点插入函数
int main(void)
{
    int n1,n2;
    List L1,L2,L_multiply,L_plus;
    scanf("%d",&n1);
    L1=input(n1);
    scanf("%d",&n2);
    L2=input(n2);
    L_multiply=multiply(L1,L2);
    L_plus=plus(L1,L2);
    output(L_multiply);
    output(L_plus);
    
    return 0;
}
List input(int n)                            //链表不带头结点
{
    List head,tail,p;
    ElementType temp_c,temp_e;
    head=tail=p=NULL;
    for (int i=0;i<n;i++) {                  //零多项式会直接返回NULL
        scanf("%d%d",&temp_c,&temp_e);
        p=(List)malloc(sizeof(struct PolyNodes));     //新建链表的基本操作 
        p->coef=temp_c;
        p->expon=temp_e;
        p->next=NULL;
        if (head==NULL)
            head=p;
        else 
            tail->next=p;
        tail=p;
    }
    
    return head;
}
void output(List const L)
{
    if (L==NULL) {                    //L指向NULL表明L是一个零多项式，特殊处理
        printf("%d %d\n",0,0);
        return;
    }
    List p=L;
    int first,tag;                    //first标记第一项输出，tag标记多项式系数是不是全为0
    first=tag=1;
    while (p) {
        if (p->coef != 0 && first) {  //只有非零项才会输出
            printf("%d %d",p->coef,p->expon);
            first=0;
            tag=0;
        } else if (p->coef != 0) {
            printf(" %d %d",p->coef,p->expon);
            tag=0;
        }
        p=p->next;
    }
    if (tag)                         //系数全是0，说明是一个零多项式
        printf("%d %d",0,0);
    printf("\n");
}
List plus(List const L1, List const L2)
{
    List head,tail,p,p1,p2;
    head=tail=p=NULL;
    p1=L1,p2=L2;
    if (p1==NULL) {                 //存在零多项式相加的情况，要特殊处理
        head=p2;
        return head;
    } else if (p2==NULL) {
        head=p1;
        return head;
    }
    while (p1 && p2) {
        p=(List)malloc(sizeof(struct PolyNodes));
        if (p1->expon == p2->expon) {
            p->coef = p1->coef+p2->coef;
            p->expon = p1->expon;
            p1 = p1->next;
            p2 = p2->next;
        } else if (p1->expon > p2->expon) {
            p->coef = p1->coef;
            p->expon = p1->expon;
            p1 = p1->next;
        } else {
            p->coef = p2->coef;
            p->expon = p2->expon;
            p2 = p2->next;
        }
        p->next=NULL;
        if (head==NULL)
            head=p;
        else 
            tail->next=p;
        tail=p;
    }
    if (p1)                       //存在两个多项式项数不等的情况，要考虑在内
        tail->next=p1; 
    else if (p2) 
        tail->next=p2;
    
    return head;
}
List multiply(List const L1, List const L2)
{
    if (L1==NULL || L2==NULL)
        return NULL;
    List head,tail,p,p1,p2;
    head=tail=p=NULL;
    p1=L1,p2=L2;
    while (p2) {                       //先得到一个降幂排列的部分链表
        p=(List)malloc(sizeof(struct PolyNodes));
        p->coef = p1->coef*p2->coef;
        p->expon = p1->expon+p2->expon;
        p->next=NULL;
        if (head==NULL)
            head=p;
        else 
            tail->next=p;
        tail=p;
        p2=p2->next;
    }
    p1=L1->next;
    while (p1) {                      //依次有序插入其他项
        p2=L2;
        while (p2) {
            p=(List)malloc(sizeof(struct PolyNodes));
            p->coef = p1->coef*p2->coef;
            p->expon = p1->expon+p2->expon;
            p->next=NULL;
            head=insert(head,p);       //通过调用插入函数解决合并同类项和降幂排列的问题
            p2=p2->next;
        }
        p1=p1->next;
    }
    
    return head;
}
List insert(List L, List X)
{
    if (X->expon > L->expon) {             //插入位置是第一个结点
        X->next=L;
        L=X;
        return L;
    }
    List p2=L,p1;
    while ( (X->expon < p2->expon) && (p2->next!=NULL) ) {   //找到待插入的位置，插入操作在后面执行
        p1=p2;
        p2=p1->next;
    }
    if (X->expon == p2->expon) {           //合并同类项
        p2->coef += X->coef;
        free(X);                           //合并同类项应释放原来的空间（因为不需要该空间了）
    } else if (X->expon > p2->expon) {     //中间插入
        X->next=p2;
        p1->next=X;
    } else {                               //在尾结点后插入
        p2->next=X;
    }
    
    return L;
}

3. 02-线性结构3 Reversing Linked List (25 分)

【题目描述】

题目链接

【题解】

【2021.05.14更新】这道题目开始的时候用的是排序的思维，虽然做出来了，但是其实是不对的，没有真正实现链表的反转。后面陈越姥姥专门讲了这道题，说排序思维是错的，还安排了“冗余数据”来卡这种错误算法，不过还是被“聪明的同学”钻了空子，用统计链表真实结点数目的方法给破解了。。（哈哈）。但是还是要按陈越姥姥的本意真正的实现一个单链表的逆转，而且姥姥的方法更加简洁明了，通用性强，而且会让你对内存、指针和链表的抽象概念有更进一步的认识。

就像姥姥说的，链表的本质还是一种抽象的数据结构，并不是说没有指针这种类型就不存在链表了，我的代码中就没有用实际的指针，而是用int类型来代表了一个指针，他照样可以实现指针的功能。这真叫温故而知新啊，哈哈~

上次的代码和思路放在另一篇文章中了（文章传送门），并且做了一个对比，下面是这次的代码：

#include 
#define MaxSize 100000
#define null -1
struct Node {      //存放结点数据 
	int Data;
	int NextAdd;
}A[MaxSize];       //数组A定义为了全局变量，模拟真实的内存环境 
int Reverse(int Head,int times,int K);
int Count(int head);
void print(int head);

int main(void)
{
	int Head,N,K,Add;
	scanf("%d%d%d",&Head,&N,&K);
	
	for (int i=0;i<N;i++) {			//读入数据 
		scanf("%d",&Add);
		scanf("%d%d",&A[Add].Data,&A[Add].NextAdd);
	}
	int times=Count(Head)/K;		//需要知道执行几次反转操作，否则多次反转无法实现 
	int New=Reverse(Head,times,K);	//进行反转 
	print(New);						//打印结果 
	
	return 0;
}

int Reverse(int Head,int times,int K)
{
	int New,TmpNew,Old,Tmp,Tail,cnt;	//New,TmpNew,Old,Tmp,Tail均起到指针的作用；cnt是计数器 
	
	for (int i=0;i<times;i++) {
		cnt=1;							//初始化
		TmpNew=Head;			
		Old=A[TmpNew].NextAdd;
		while (cnt<K) {					//依次反转 
			Tmp=A[Old].NextAdd;
			A[Old].NextAdd=TmpNew;
			TmpNew=Old;
			Old=Tmp;
			cnt++;
		}
		if (i==0)				//第一次反转的TmpNew是真正的New 
			New=TmpNew;
		A[Head].NextAdd=Old;
		if (i==0)				//需要把上次反转的尾巴的Next指针指到TmpNew 
			Tail=Head;
		else {
			A[Tail].NextAdd=TmpNew;
			Tail=Head;
		}
		Head=Old;
	}
	
	return New;
}
int Count(int head)		//统计链表的真实结点数目 
{
	int sum,p;
	p=head,sum=0;
	while (p!=null) {
		sum++;
		p=A[p].NextAdd;
	}
	return sum;
}
void print(int head)	//打印链表元素 
{
	int p=head;
	while (p!=null) {
		if (A[p].NextAdd!=null)  //输出格式控制 
			printf("%05d %d %05d\n",p,A[p].Data,A[p].NextAdd);
		else
			printf("%05d %d %d\n",p,A[p].Data,A[p].NextAdd);
		p=A[p].NextAdd;
	}
}

4. 02-线性结构4 Pop Sequence (25 分)

【题目描述】

题目链接

【题解】

这道题目想了两三天没想通，结果晚上和人交流的时候突然灵光一现，发现了一种解决方法，就是利用”模拟实现“的思路，即”模拟计算机实现题目所描述的过程，进而发现解决该问题的方法“。第二天迅速打代码，结果打码二十分钟，debug了两个多小时。。。最后发现最大的问题是堆栈创建的位置不对，应该在JudgeStack函数里创建，不应该在main函数中创建，因为每次判断都需要一个新的堆栈，如果在主函数中创建，那么堆栈中可能遗留有上次的输入的残余，所以这也是为什么我有一个测试序列老是不对的原因，唉，嘴上说还是不能和上手打一样啊！

下面再说说解题思路：

• 找规律：刚开始我想的是找出数学规律，然后来判断是否是可能的输出序列。但是这种方式太困难了，反正我按照这个思路是想不出来的，如果有能想出来的大佬麻烦告诉我一声，哈哈~

• 模拟实现：后面想到的办法就是模拟实现，具体来说就是就是模拟计算机的push和pop过程，看看能否得到一个与测试序列一样的pop序列（注意肯定不是一次性push和一次性pop，那样有且仅有一种可能的输出序列，就是7654321这种倒序）。

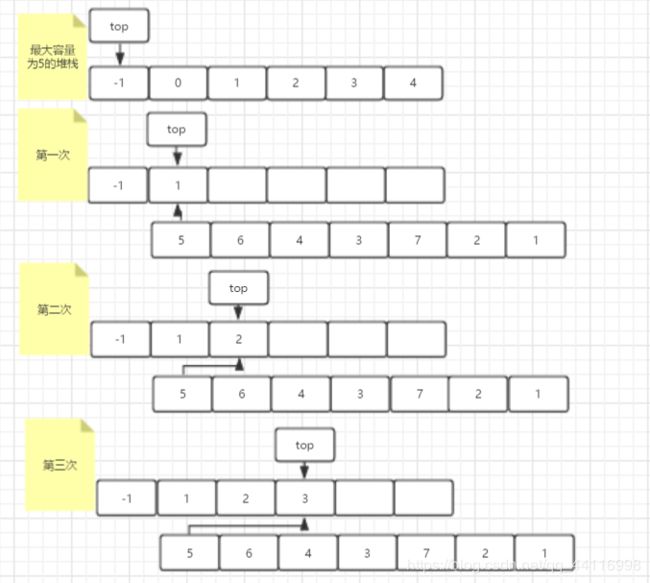
  举个例子，比如给的是5 6 4 3 7 2 1，那么按照1 2 3 4 5 6 7的顺序入栈，中间随机pop。设置一个计数器cnt（初始化为0），用于最后比较是否完全得到了输出序列。先push第一个数num进入堆栈，之后比较栈顶元素Top和输出序列数组元素output[j]是否相等。如果相等，则j++，同时cnt++；如果不相等，则继续push下一个数（num++）进去（在这之前要把pop的数Top先push回来），然后继续比较。循环条件是(num<=N && j

  整个过程的图解如下图所示（图是从这篇文章拷贝过来的）：

  

具体代码如下：

#include 
#include 
#include 
/*堆栈代码块*/ 
#define ElementType_Stack int
typedef int Position;
typedef struct StackNode* Stack;
struct StackNode {
	ElementType_Stack *Data;
	Position Top;
	int MaxSize;
};
Stack CreateStack(int MaxSize);
bool IsFull(Stack S);
bool IsEmpty(Stack S);
bool Push(Stack S,ElementType_Stack X);
ElementType_Stack Pop(Stack S);
/*Judge函数声明*/
bool JudgeStack(int M,ElementType_Stack output[],int N);
/*主函数*/ 
int main (void)
{
	int M,N,K;
	scanf("%d%d%d",&M,&N,&K);
	ElementType_Stack output[N];
	int k,num,mark[K];                  //mark数组保存判断结果 
	k=K;
	while (k--) {
		for (int i=0;i<N;i++) {         //读入待判断的pop序列 
			scanf("%d",&num);
			output[i]=num;
		}
		if (JudgeStack(M,output,N)) {   //判断是否是可能的pop序列 
			mark[k]=1;
		} else {
			mark[k]=0;
		}
	}
	k=K; 
	while (k--) {                       //输出判断结果 
		if (mark[k]) {
			printf("YES\n");
		} else {
			printf("NO\n");
		}
	}
	
	return 0;
}
/*Judge函数*/ 
bool JudgeStack(int M,ElementType_Stack output[],int N)
{
	int num,j,cnt;                	//num表示输入序列 
	ElementType_Stack Top;        	//Top：栈顶元素 
	Stack S=CreateStack(M);			//必须在这里创建栈 
	num=1;
	j=cnt=0;
	Push(S,num);					//push第一个数进入堆栈 
	while (num<=N && j<N) {
		Top=Pop(S);
		if (Top==output[j]) {		//栈顶元素==输出序列 
			cnt++;
			j++;
		} else {					//不相等 
			if (Top>0)				//记得先取回已经pop的数 
				Push(S,Top);
			num++;
			Push(S,num);			//push下一个输入序列的数 
		}
	}
	if (cnt==N)						//cnt==N表明完全得到了输出序列 
		return true;				//栈溢出的话肯定会使num>N且cnt!=N，所以不用单独判断 
	else
		return false;
}
/*堆栈代码块*/ 
Stack CreateStack(int MaxSize)
{
	Stack S=(Stack)malloc(sizeof(struct StackNode));
	S->Data=(ElementType_Stack*)malloc(MaxSize*sizeof(ElementType_Stack));
	S->Top=-1;
	S->MaxSize=MaxSize;
	return S;
}
bool IsFull(Stack S)
{
	return (S->Top==S->MaxSize-1);
}
bool IsEmpty(Stack S)
{
	return (S->Top==-1);
}
bool Push(Stack S,ElementType_Stack X)
{
	if (IsFull(S)) {
		return false;
	} else {
		S->Data[++(S->Top)]=X;
		return true;
	}
}
#define ERROR -1
ElementType_Stack Pop(Stack S)
{
	if (IsEmpty(S)) {
		return ERROR;
	} else {
		return S->Data[(S->Top)--];
	}
}