机器学习基础学习-多项式回归

前言

之前的线性回归法有一个很大的局限性，要求假设数据背后是存在线性关系的，但是对于实际应用场景当中，具有线性关系比较强的数据集太少了，更多的是具有非线性关系的数据集。
这里引入使用多项式回归，改进线性回归法，可以对非线性的数据进行处理，进而进行预测（进而其实可以引出模型泛化这个概念）

1、多项式回归概念

我们学习线性回归时，对于这些数据，我们想要找一条直线，让这条直线尽可能的拟合这些数据，如果这些数据只有一个特征的话，相应的直线就是y=ax+b，x是样本特征，a和b就是我们需要求的模型参数。
但是对于有一些数据，例如

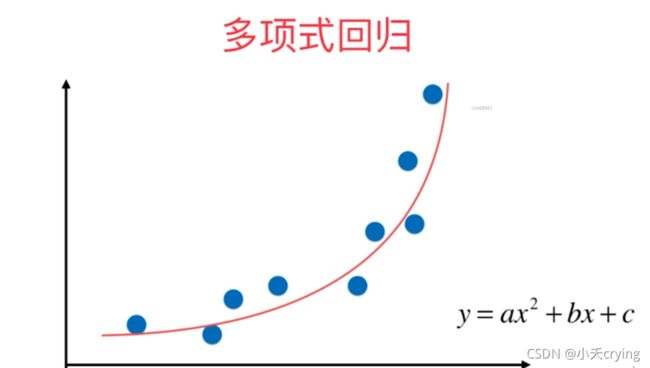
其实我们也可以通过线性回归的方式来拟合数据，但是其实他有更强的非线性的关系（用这样一个二次曲线y=ax² +bx+c来拟合，效果会更好）

对于这个式子，从另一个角度来理解，将x² 理解成一个特征，x理解成另外一个特征，本来我们的样本特征只有一个特征x，现在我们把它看成有两个特征的数据集，我们多了一个x² 的特征，从这个角度看，这个式子仍然是一个线性回归的例子，但是从x的角度看是一个非线性的方程，这样的过程就叫做多项式回归（相当于我们为样本多添加了一些特征，这些特征是原来样本的多项式项，增加这些特征后，我们可以用线性回归的方式更好的拟合原来的数据，但是本质上求出了我们对于原来的特征而言的非线性的曲线）

2、实现过程

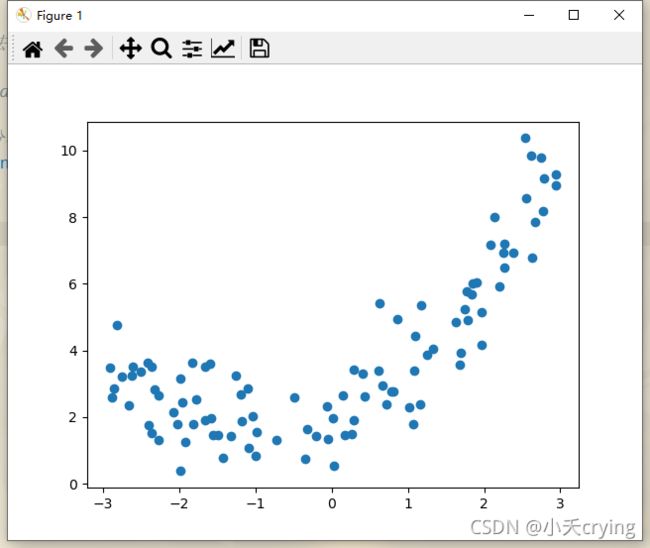
1、生成随机样本并绘制

import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
# random.uniform(x, y)方法将随机生成一个实数，它在 [x,y] 范围内。
x = np.random.uniform(-3, 3, size = 100)
X = x.reshape(-1, 1) # shape：（100,1）

# np.random.normal()正态分布的噪音
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)

# 绘制样本
plt.scatter(x, y)
plt.show()

此时我们的样本输出y和样本特征x之间是一个非线性的关系。

2、线性回归拟合数据集
同样，在此之前，我们把之前定义过的线性回归的类，单独存放在一个文件，然后需要的时候直接调用即可。下面是线性回归类的代码，可以参考机器学习基础学习-多元线性回归问题（数学解实现）、机器学习基础学习-多元线性回归问题（梯度下降法实现）

# 线性回归类

import numpy as np
from sklearn.metrics import r2_score

class LinearRegression:
  def __init__(self):
      # 初始化Linear Regression模型
      self.coef_ = None # 系数，对应theta1-n，对应的向量
      self.interception_ = None # 截距，对应theta0
      self._theta = None # 定义私有变量，整体计算的theta



  '''
    梯度下降
  '''
  def fit_gd(self, X_train, y_train, eta = 0.01, n_iters = 1e4): 
    # 根据训练数据集X_train, y_ .train训练Linear Regression模型
    # X_train的样本数量和y_train的标记数量应该是一致的
    # 使用shape[0]读取矩阵第一维度的长度，在这里就是列数
    assert X_train.shape[0] == y_train.shape[0], \
    "the size of x_ .train must be equal to the size of y_ train"
    # 损失函数
    def J(theta, X_b, y):
      try:
        return np.sum((y - X_b.dot(theta)) ** 2 / len(y))
      except:
        return float('inf') # 返回float最大值

    # 梯度(比较笨的方法)
    def dJ(theta, X_b, y):
      res = np.empty(len(theta)) # 开一个和theta一样大的空间(因为要对theta的每一个元素求偏导)
      res[0] = np.sum(X_b.dot(theta) - y) # 第一行单独写，其他的要写一个循环
      for i in range(1, len(theta)):
        res[i] = (X_b.dot(theta) - y).dot(X_b[:,i]) # X_b[:,i]相当于取出第i列，也就是第i个特征值
      return res * 2 / len(X_b)


    # 求解theta矩阵
    def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon = 1e-8):
      theta = initial_theta
      cur_iters = 0

      while cur_iters < n_iters:
          gradient = dJ(theta, X_b, y) # 求梯度
          last_theta = theta # theta重新赋值前，记录上一场的值
          theta = theta - eta * gradient # 通过一定的eta学习率取得下一个点的theta
          # 最近两点的损失函数差值小于一定精度，退出循环
          if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
              break
          cur_iters += 1
      return theta

    # 得到X_b
    X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
    initial_theta = np.zeros(X_b.shape[1]) # 设置n+1维的向量,X_b.shape[1]:第一行的维数
    # X_b.T是X_b的转置,.dot是点乘,np.linalg.inv是求逆
    # 获取theta
    self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

    self.interception_ = self._theta[0] # 截距
    self.coef_ = self._theta[1:] # 系数 
    return self




  '''
    解析解
  '''
  # 正规化方程
  # 训练过程（解析解）
  def fit_normal(self, X_train, y_train): # X_train和y_train都是矩阵
    # 根据训练数据集X_train, y_ .train训练Linear Regression模型
    # X_train的样本数量和y_train的标记数量应该是一致的
    # 使用shape[0]读取矩阵第一维度的长度，在这里就是列数
    assert X_train.shape[0] == y_train.shape[0], \
    "the size of x_ .train must be equal to the size of y_ train"
    # np.hstack():在水平方向上平铺，就是在横向上多加一列
    # np.ones(矩阵大小, 列数)是增加一列恒为1的一列
    # 得到X_b
    X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
    # X_b.T是X_b的转置,.dot是点乘,np.linalg.inv是求逆
    self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)

    self.interception_ = self._theta[0] # 截距
    self.coef_ = self._theta[1:] # 系数
    return self
  
  '''
    预测过程
  '''
  def predict(self, X_predict):
    # 给定待预测数据集X_predict,返回表示X_predict的结果向量
    X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
    return X_b.dot(self._theta)

  '''
    确定精度，评价多元线性回归的结果
  '''
  def score(self, X_test, y_test):
    # 根据测试数据集X_test 和y_test 确定当前模型的准确度
    y_predict = self.predict(X_test)
    return r2_score(y_test, y_predict) # r2_score求真值y_test和预测值y_predict的r方

  '''
    显示属性
  '''
  def __repr__(self):
      return "LinearRegression()"

需要的时候进行调用

from classLinearRegression import LinearRegression # 引入线性回归类对象

# 实例化对象
lin_reg = LinearRegression()
# 训练
lin_reg.fit_normal(X, y)

下面的是进行线性回归的过程

'''
  线性回归拟合数据集
  不划分测试集与训练集，所有样本送去训练
'''
# 实例化对象
lin_reg = LinearRegression()
# 训练
lin_reg.fit_normal(X, y)
y_predict = lin_reg.predict(X)
# 预测
print(y_predict, 'y_predict')
# 绘制预测后的结果
plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()

回归结果

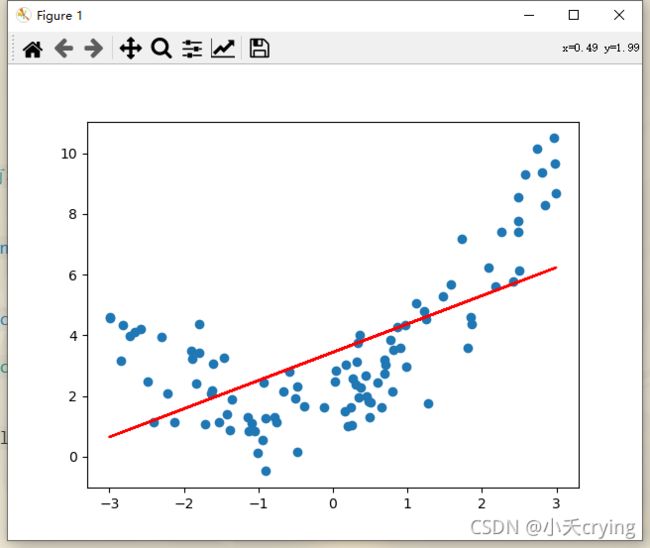
很明显，我们用这样一根直线来拟合有弧度的曲线，这样的拟合效果是不够好的，所以我们通过多项式回归的方式，添加一个特征来拟合效果会更好

3、多项式回归拟合数据集

1、添加新的特征
现在我们添加一个特征，原来所有的特征都在X中，现在我们对X中的每一个数据都进行平方，那么X²本身就是一列新的特征

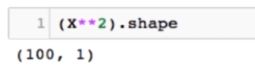
接下来我们通过hstack将原来的X和X² 合并成一个矩阵

# np.vstack():在竖直方向上堆叠
# np.hstack():在水平方向上平铺
X2 = np.hstack([X, X**2])

这时X2是100行2列的矩阵，相当于我们通过原来的数据集创建了一个新的数据集，原来的数据集中每个样本只有一个特征，现在新的数据集当中每个样本有两个特征，然后我们对这个新的数据集进行线性回归的训练。
2、进行训练
首先展示一个小错误

'''
  多项式回归
'''
# np.vstack():在竖直方向上堆叠
# np.hstack():在水平方向上平铺
X2 = np.hstack([X, X**2])
# 实例化新对象
lin_reg2 = LinearRegression()
lin_reg.fit_normal(X2, y)
y_predict2 = lin_reg.predict(X2)
print(y_predict2, 'y_predict2多项式回归预测结果')
# 绘制多项式回归，预测后的结果
plt.scatter(x, y)
plt.plot(x, y_predict2, color='r')
plt.show()

出来的结果

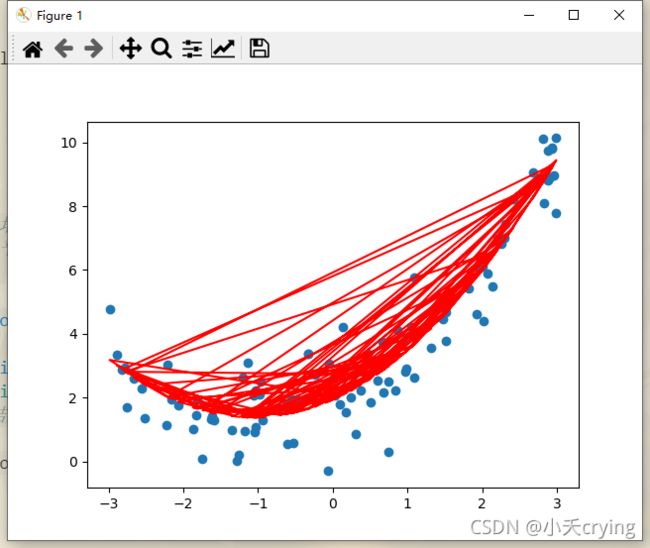
这里生成的折线图是乱的，这是因为生成的x是没有顺序的，如想生成平滑的曲线，我们需要对x进行排序，要把x从小到大进行排序，对于y_predict2，我们也应该找到对应排序后的x对应的y_predict2的预测值

# argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')

修改后的代码

'''
  多项式回归
'''
# np.vstack():在竖直方向上堆叠
# np.hstack():在水平方向上平铺
X2 = np.hstack([X, X**2])
# 实例化新对象
lin_reg2 = LinearRegression()
lin_reg.fit_normal(X2, y)
y_predict2 = lin_reg.predict(X2)
print(y_predict2, 'y_predict2多项式回归预测结果')
# 绘制多项式回归，预测后的结果
plt.scatter(x, y)
# argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()

绘制结果

总结

其实多项式回归的思路就是将原来的数据的X特征矩阵中多加了一个特征，这个特征是我们自己认为造的（将原来所有样本的特征进行了平方），当我们添加这个特征后，从x的维度看，形成了一条曲线，这条曲线对我们的数据集的拟合程度是更高的。
我们也可以查看我们求得的theta系数矩阵

这里两个系数差不多接近1和0.5，对应我们的样本特征来说，第一列相当于是X本身，第二列是X² ,他们的系数分别是1和0.5，对比我们生成样本前的系数
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)
所以我们经过训练后得到的系数和生成数据的方式是整体拟合的，有细微的偏差是因为我们生成数据的时候添加了部分噪音，进行拟合的时候考虑到了这部分的噪音所以产生了部分的偏差。
接下来查看截距

和我们生成样本的截距也是一致的
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)

多项式回归在机器学习上其实并没有新的东西，完全是使用线性回归的思路，关键在于我们为原来的数据样本添加了新的特征，而得到这些新的特征的方式是将原有的特征进行多项式组合，采用这样的方式就可以解决一些非线性的问题（一种升维操作，在升高维度后，使得算法更好拟合高纬度数据）。

最后附上整体的代码（LinearRegression 类的代码在上面有）

# 多项式回归

import numpy as np
import matplotlib.pyplot as plt
from classLinearRegression import LinearRegression # 引入线性回归类对象

# 生成随机数据
# random.uniform(x, y)方法将随机生成一个实数，它在 [x,y] 范围内。
x = np.random.uniform(-3, 3, size = 100)
X = x.reshape(-1, 1) # shape：（100,1）

# np.random.normal()正态分布的噪音
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)

# 绘制样本
plt.scatter(x, y)
plt.show()



'''
  线性回归拟合数据集
  不划分测试集与训练集，所有样本送去训练
'''
# 实例化对象
lin_reg = LinearRegression()
# 训练
lin_reg.fit_normal(X, y)
y_predict = lin_reg.predict(X)
# 预测
print(y_predict, 'y_predict')
# 绘制预测后的结果
plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()


'''
  多项式回归
'''
# np.vstack():在竖直方向上堆叠
# np.hstack():在水平方向上平铺
X2 = np.hstack([X, X**2])
# 实例化新对象
lin_reg2 = LinearRegression()
lin_reg.fit_normal(X2, y)
y_predict2 = lin_reg.predict(X2)
print(y_predict2, 'y_predict2多项式回归预测结果')
# 绘制多项式回归，预测后的结果
plt.scatter(x, y)
# 直接绘制，会导致图像错乱，因为x，y的值没有按照大小顺序排序
# plt.plot(x, y_predict2, color='r')
# argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()