公式推导:

代码实现:
import matplotlib.pyplot as plt
import numpy as np
def f(w1,x1,w2,x2,b):
z=w1*x1+w2*x2+b
return 1/(1+np.exp(-z))
if __name__ == '__main__':
X1 =[12.46, 0.25, 5.22, 11.3, 6.81, 4.59, 0.66, 14.53, 15.49, 14.43,
2.19, 1.35, 10.02, 12.93, 5.93, 2.92, 12.81, 4.88, 13.11, 5.8,
29.01, 4.7, 22.33, 24.99, 18.85, 14.89, 10.58, 36.84, 42.36, 39.73,
11.92, 7.45, 22.9, 36.62, 16.04, 16.56, 31.55, 20.04, 35.26, 23.59]
X2 =[29.01, 4.7, 22.33, 24.99, 18.85, 14.89, 10.58, 36.84, 42.36, 39.73,
11.92, 7.45, 22.9, 36.62, 16.04, 16.56, 31.55, 20.04, 35.26, 23.59,
12.46, 0.25, 5.22, 11.3, 6.81, 4.59, 0.66, 14.53, 15.49, 14.43,
2.19, 1.35, 10.02, 12.93, 5.93, 2.92, 12.81, 4.88, 13.11, 5.8]
Y= []
for i in range(len(X1)):
if X1[i]+X2[i]<20:Y.append(0)
else:Y.append(1);
w1=1
w2=-1
b=2
a=5
w1_temp=-100
w2_temp = -100
b_temp=-100
w1change = 100
w2change = 100
bchange = 100
while abs(w1change)>1e-6 and abs(w2change)>1e-6 and abs(bchange)>1e-6:
print(w1change)
w1change=0
w2change=0
bchange=0
for i in range(len(X1)):
w1change+=(f(w1,X1[i],w2,X2[i],b)-Y[i])*X1[i]
w2change += (f(w1,X1[i],w2,X2[i],b) - Y[i]) * X2[i]
bchange+=(f(w1,X1[i],w2,X2[i],b) - Y[i])
w1change/=len(X1)
w2change /= len(X2)
bchange /= len(X1)
w1_temp=w1-a*w1change
w2_temp = w2 - a * w2change
b_temp=b-a*bchange
w1=w1_temp
w2 = w2_temp
b=b_temp
print("y=%.4f*x1+%.4f*x2+%.4f" % (w1,w2, b))
X1_1 = []
X1_2 = []
X2_1 = []
X2_2 = []
for i in range(len(X1)):
if(Y[i]==0):
X1_1.append(X1[i])
X2_1.append(X2[i])
else:
X1_2.append(X1[i])
X2_2.append(X2[i])
print(X1_1)
plt.scatter(X1_1, X2_1, c="blue")
plt.scatter(X1_2, X2_2, c="red")
x = np.linspace(0, 40, 200)
y=(w1*x+b)/(-w2)
plt.plot(x,y)
plt.show()
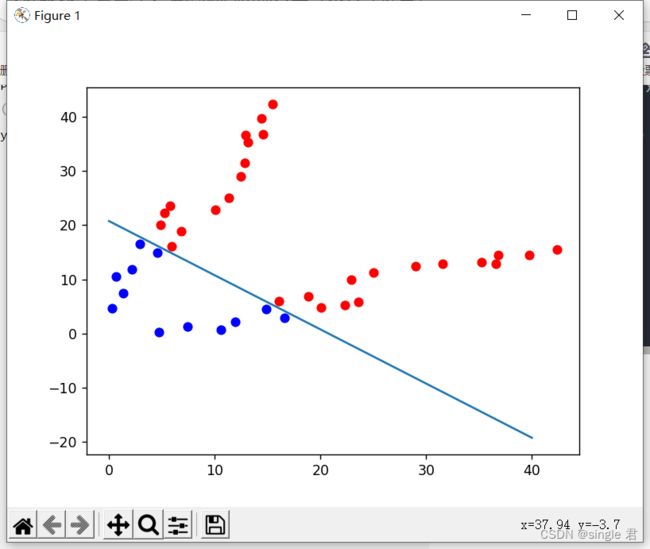
效果还不错,我感觉逻辑回归的最佳学习率要比线性回归最佳学习率大多了。

