汉诺塔问题详解【C语言递归】

简介：

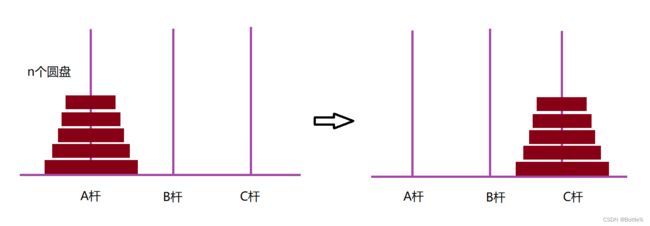
汉诺塔问题，即在一个装置上有A，B，C三根杆。在A杆自下而上、由大到小按顺序放置n个圆盘（如下图），我们需要保存原有顺序把A杆上的圆盘全部移到C杆上。

操作过程中，每次只能移动一个圆盘，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

我们就用递归思想来计算该问题中圆盘移动次数和步骤。

思路：

我们先列举几种情况来明确我们的思路：

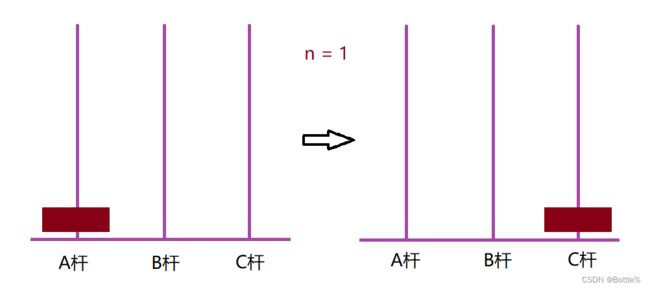
当圆盘个数 n = 1时：

即只有一个圆盘时，将红色圆盘从所在杆A移动到目标杆C，只需要移动1次即可。

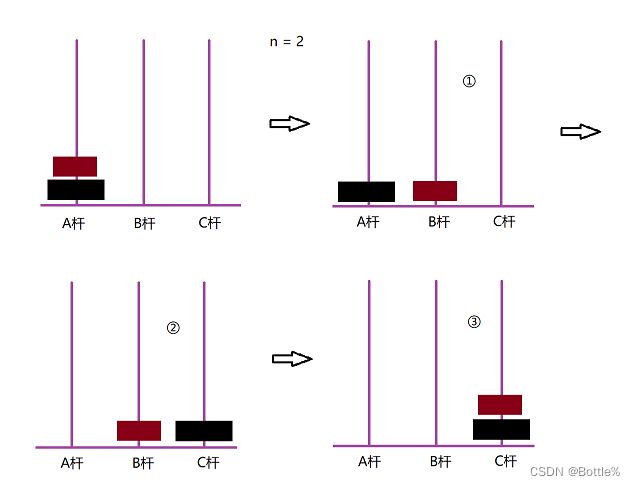
当 圆盘个数 n = 2时：

第一步：把上层的红色圆盘从所在杆A移到中间杆B上。

第二步：把底层的黑色圆盘从所在杆A移动到目标杆C上。

第三步：把红色圆盘从所在杆B上移动到目标杆C上。（如下图）

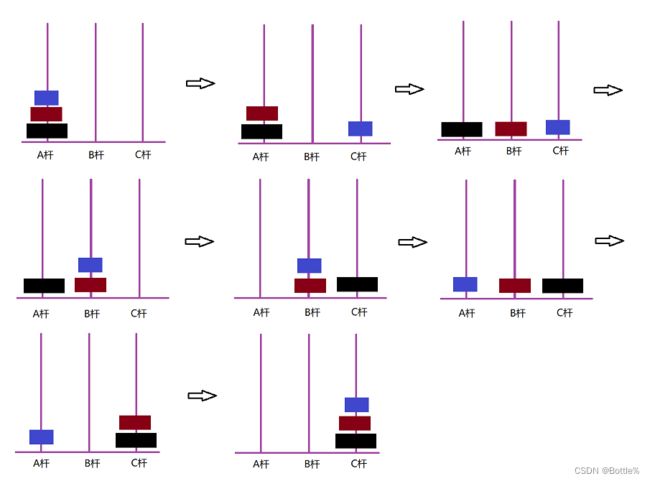
 当 圆盘个数 n = 3时：

 步骤如下图

我们把黑色上方的蓝色、红色两个圆盘看成一个整体，那么这个过程即可简化成与n=2时相同的情况，只需三步即可。

第一步：把上层的红色和蓝色圆盘从所在杆A移到中间杆B上。

第二步：把底层的黑色圆盘从所在杆A移动到目标杆C上。

第三步：把红色和蓝色圆盘从所在杆B上移动到目标杆C上。

 此时，我们再把红色和蓝色圆盘拆分来看：（上述的三步）

第一步便是n = 2时的情况，只是目标杆进行了改变，从A杆移动到B杆上。

第二步把最底层的圆盘移动到目标杆C上即可，只需要移动一次。

第三步依然是重复n = 2时的情况，从B杆移动到C杆上。

由此，我们可以根据以上三个步骤将其概括为：

n = 1时，移动一次即可。

n > 1时，先将（n - 1）个圆盘看成一个圆盘，将其移动到中间杆上，移动1次最底层的圆盘至目标杆，再将（n - 1）个圆盘从中间杆移到目标杆上。如果（n - 1）> 1的话，则再次重复上述三个步骤。

归纳为公式即：

n = 1时，f（n） = 1；

n > 1时，f（n）= f（n-1）+ 1 + f（n - 1）= 2*f（n - 1）+ 1；

移动次数代码：

#include
int hanoi_num(int n)
{
	if (n > 1)
	{
		return 2 * hanoi_num(n - 1) + 1;
	}
	else
	{
		return 1;
	}
}
int main()
{
	int n;
	scanf("%d", &n);
	printf("次数为：%d", hanoi_num(n));
	return 0;
}

移动步骤：

根据上述的思路，移动的步骤在于所在杆、中间杆、目标杆这三个杆的转换。

方法步骤与上述移动次数一致：（n > 1时）

第一步：把最底层以上的所有圆盘从A杆移动到B杆上，即所在杆A、中间杆C、目标杆B。

第二步：把最底层的圆盘从所在杆A移动到目标杆C上。直接从所在杆A移动到目标杆C即可。

第三步：把最底层以上的所有圆盘从B杆移动到C杆上，即所在杆B、中间杆A、目标杆C。

如果最底层以上的所有圆盘的数量 > 1时，再分别重复上述步骤。

代码如下：

#include
void hanoi_move(int n, char A, char B, char C)
//参数A,B,C分别为所在杆，中间杆，目标杆
{
	if (n > 1)
	{
		//传入的参数为当前情况下的所在杆，中间杆，目标杆
		hanoi_move(n - 1, A, C, B);
		printf("%c -> %c\n",A,C);
		hanoi_move(n - 1, B, A, C);
	}
	else
	{
		printf("%c -> %c\n",A,C);
	}
}
int main()
{
	int n;
	scanf("%d", &n);
	hanoi_move(n,'A','B','C');
	return 0;
}

作为一名C语言初学者，有表述不清，还请多包涵。如有错误，欢迎指正。