如何设计一个 A/B test --来自腾讯数据分析师的分享
一、实验设计
AB Test 实验一般有 2 个目的:
- 判断哪个更好:例如,有 2 个 UI 设计,究竟是 A 更好一些,还是 B 更好一些,我们需要实验判定
- 计算收益:例如,最近新上线了一个直播功能,那么直播功能究竟给平台带了来多少额外的 DAU,多少额外的使用时长,多少直播以外的视频观看时长等
我们一般比较熟知的是上述第 1 个目的,对于第 2 个目的,对于收益的量化,计算 ROI,往往对数据分析师和管理者非常重要。
对于一般的 ABTest 实验,其实本质上就是把平台的流量均匀分为几个组,每个组添加不同的策略,然后根据这几个组的用户数据指标,例如:留存、人均观看时长、基础互动率等等核心指标,最终选择一个最好的组上线。
二、流量分配
实验设计时有两个目标:
- 希望尽快得到实验结论,尽快决策
- 希望收益最大化,用户体验影响最小
因此经常需要在流量分配时有所权衡,一般有以下几个情况:
- 不影响用户体验:如 UI 实验、文案类实验等,一般可以均匀分配流量实验,可以快速得到实验结论
- 不确定性较强的实验:如产品新功能上线,一般需小流量实验,尽量减小用户体验影响,在允许的时间内得到结论
- 希望收益最大化的实验:如运营活动等,尽可能将效果最大化,一般需要大流量实验,留出小部分对照组用于评估 ROI

根据实验的预期结果,大盘用户量,确定实验所需最小流量,可以通过一个网站专门计算所需样本量:https://www.evanmiller.org/ab-testing/sample-size.html
详见:如何计算A/B test样本量:
https://blog.csdn.net/weixin_41744624/article/details/109840263
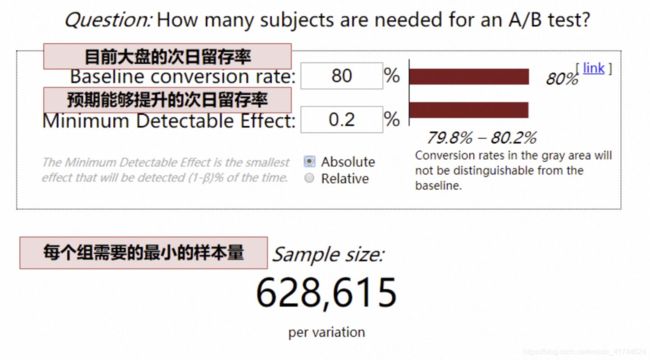
a.比例指标:
- 以次日留存率为例,目前大盘次日留存率 80%,预期实验能够提升 0.2pp(这里的留存率可以转换为点击率、渗透率等等,只要是比例值就可以,如果估不准,为了保证实验能够得到结果,此处可低估,不可高估,也就是 0.2pp 是预期能够提升地最小值)
- 网站计算,最少样本量就是 63W(这里的最少样本量,指的是最少流量实验组的样本量)
- 如果我们每天只有 5W 的用户可用于实验(5W 的用户,指最少流量实验组是 5W 用户),63/ 5 = 13 天,我们需要至少 13 天才能够得到实验结论
b.均值指标:
如果我们预期提升的指标是人均时长、人均 VV 等,可能就比较复杂了,我们需要运用 t 检验反算,需要的样本量:
https://www.evanmiller.org/ab-testing/t-test.html

三、实验效果
我们以一个稍复杂点的运营活动实验为例,活动有方案 1、方案 2,同时为了量化 ROI,对照组没有运营活动。

需要回答几个问题
- 方案 1 和方案 2,哪个效果更好?
- 哪个 ROI 更高?
- 长期来看哪个更好?
- 不同群体有差异吗?
第 1 个问题,方案 1 和方案 2,哪个效果更好?
还是要运用假设检验,对于留存率、渗透率等漏斗类指标,采用卡方检验:
https://www.evanmiller.org/ab-testing/chi-squared.html
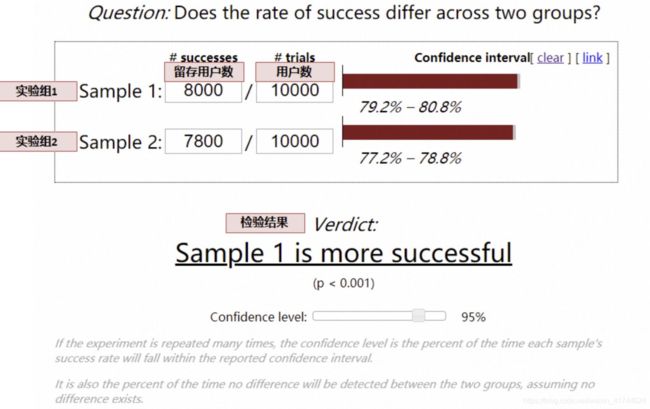
对于人均时长类等均值类指标,采用t 检验:

通过上假设检验,如果结论置信,我们就能够得到方案 1 和方案 2 在哪像指标更好(有显著性差异), 对于不置信的结论,尽管方案 1 和方案 2 的指标可能略有差异,但可能是数据正常波动产生。
第 2 个问题,哪个 ROI 更高?
一般有活动相比无活动,留存、人均时长等各项指标均会显著,我们不再重复上述的假设检验过程。
对于 ROI 的计算,成本方面,每个实验组成本可以直接计算,对于收益方面,就要和对照组相比较,假定以总日活跃天(即 DAU 按日累计求和)作为收益指标,需要假设不做运营活动,DAU 会是多少,可以通过对照组计算,即:
- 实验组假设不做活动日活跃天 = 对照组日活跃天 * (实验组流量 / 对照组流量)
- 实验组收益 = 实验组日活跃天 - 实验组假设不做活动日活跃天
这样就可以量化出每个方案的 ROI。
第 3 个问题,长期来看哪个更好?
这里就要考虑新奇效应的问题了,一般在实验上线前期,用户因为新鲜感,效果可能都不错,因此在做评估的时候,需要观测指标到稳定态后,再做评估。

例如有的时候出现,刚刚上线前期,实验组效果更好,但是经过以端时间,用户的新鲜感过去了,实验组的效果可能更差,因此,从长远收益来看,我们应该选择对照组,是实验组的新奇效应欺骗了我们,在做实验分析时,应剔除新奇效应的部分,待平稳后,再做评估
第 4 个问题,不同用户群体有差异吗?
很多情况下,对新用户可能实验组更好,老用户对照组更好;对年轻人实验组更好,中年人对照组更好,
作为数据分析师,分析实验结论时,还要关注用户群体的差异。
四、实验结束
实验结束后需要:
- 反馈实验结论,包括直接效果(渗透、留存、人均时长等)、ROI
- 充分利用实验数据,进一步探索分析不同用户群体,不同场景下的差异,提出探索性分析
- 对于发现的现象,进一步提出假设,进一步实验论证
a.更高级的实验
对于长线业务,可能同时有数十个实验同时进行,不但对比每项小迭代的差异,同时对比专项对大盘的贡献量、部门整体对大盘的贡献量,这样就需要运用到了实验的层域管理模型。
- 对比每个产品细节迭代的结果
- 对比每个专项在一个阶段的贡献
- 对比整个项目在一个阶段的贡献
b.多个活动交集量化的实验设计
作为数据分析师,多团队合作中,经常遇到多业务交集的问题,以我近期主要负责的春节活动为例,老板会问:
- 春节活动-明星红包子活动贡献了多少 DAU?春节活动-家乡卡子活动贡献了多少 DAU?
- 春节活动总共贡献了多少 DAU?
严谨一点,我们采用了 AB 实验的方式核算,最终可能会发现一个问题:春节活动各个子活动的贡献之和,不等于春节活动的贡献,为什么呢?
- 有的时候,活动 A 和活动 B,有着相互放大的作用,这个时候就会 1+1 > 2
- 还有的时候,活动 A 和活动 B,本质上是在做相同的事情,这个时候就会 1+1 < 2
这个时候,我们准确量化春节活动的贡献,就需要一个【贯穿】所有活动的对照组,在 AB 实验系统中通俗称作贯穿层。
(说明:实验中,各层的流量是正交的,简单理解,例如,A 层的分流采用用户 ID 的倒数第 1 位,B 层的分流采用用户 ID 的倒数第 2位,在用户 ID 随机的情况下,倒数第 1 位和倒数第 2 位是没有关系的,也称作相互独立,我们称作正交。当然,AB Test 实验系统真实的分流逻辑,是采用了复杂的 hash 函数、正交表,能够保证正交性。)
这样分层后,我们可以按照如下的方式量化贡献:
- 计算春节活动的整体贡献:实验填充层-填充层填充组 VS 贯穿层-贯穿层填充组
- 计算活动 A 的贡献:活动 A 实验层中,实验组 VS 对照组
- 计算活动 B 的贡献:活动 B 实验层中,实验组 VS 对照组
c.业务迭代的同时,如何与自身的过去比较
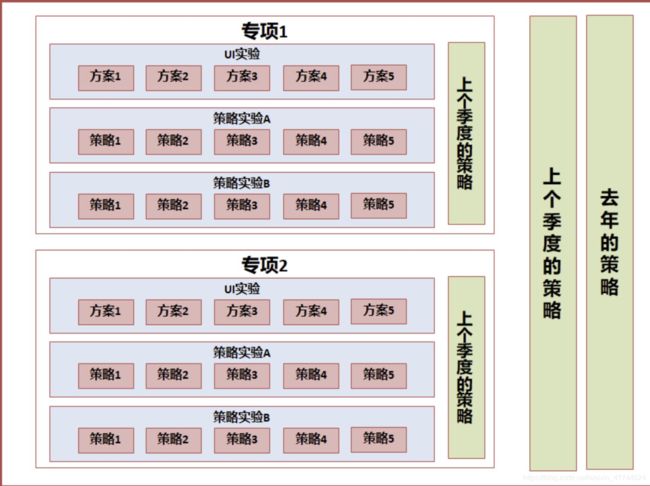
上面谈到了【贯穿层】的设计,贯穿层的设计其实不但可以应用在多个活动的场景,有些场景,我们的业务需要和去年或上个季度的自身对比,同时业务还不断在多个方面运用 AB Test 迭代。

类似与上面这种层次设计,在推荐系统中较为常见,在某一些产品或系统中,贯穿层不能够完全没有策略,那么采用去年或上个季度的策略,代表着基准值,从而量化新一个周期的增量贡献
我们可以量化:
- 每个小迭代对整个系统的贡献:实验层中的实验组 VS 对照组
- 周期内,系统全部迭代与上个周期的比较:实验填充层 VS 贯穿层 1(或贯穿层 2)
- 同时,可以量化去年策略的自然增长或下降,以衡量旧有系统是否具有长期的适用性(作为系统设计者,更应鼓励设计具有长期适应性的系统):贯穿层1(上个季度的策略)VS 贯穿层 2(去年的策略)
d.更为复杂的实验设计
我以我目前负责的业务,微视任务福利中心的实验设计为例,举例一个更复杂的实验系统设计,综合了上面提到的 2 个目的:
- 量化每一个实验迭代为系统带来的增量贡献
- 量化每一类迭代(如 UI 迭代、策略迭代),在一个阶段的增量贡献
- 量化系统整体在上一个周期(季度、年)的增量贡献
- 量化任务福利中心的整体 ROI(本质上,是给用户一些激励,促进用户活跃,获得更多商业化收益,所以和推荐系统不同的是,需要有完全没有任务福利中心的对照组,用户量化 ROI)