2023年河北省研究生数学建模竞赛D题中国钢铁工业低碳转型与高质量发展路径优化研究思路和代码
D题中国钢铁工业低碳转型与高质量发展路径优化研究
目前已写出D题初步代码,下载地址:【2023年河北省研究生数学建模竞赛D题初步思路和代码-哔哩哔哩】 https://b23.tv/g2ATbX5
随着我国工业化、城镇化进程的加快和消费结构持续升级,能源需求刚性增 长,资源环境问题日趋严峻,节能减排已成为国家发展战略的重中之重。钢铁行 业是能源消耗大户和碳排放大户,节能减排效果对我国相关战略目标的实现及环 境治理至关重要,已成为人们普遍关注的热点。在全球低碳发展背景下,走节能 减排低碳绿色发展之路已成为中国钢铁工业的必然选择。
近年来,我国钢铁行业在降低能源消耗、减少污染物排放、发展绿色制造方 面取得了显著成效,但还存在很多难题。而解决这些难题,迫切需要有先进技术 的支撑,需要科学的方向性指引,需要从技术层面加以激励,形成钢铁行业绿色 低碳高质量发展的重要推动力。
低碳发展意义重大,它将对钢铁行业产生深远影响,甚至带来广泛而深刻的 变革,进而重塑区域乃至全球钢铁发展格局。因此,探究世界钢铁工业低碳发展 的影响因素对缓解工业过程中的排放问题具有重要指导意义。
钢铁工业存在高污染、高排放的共性,影响钢铁工业CO2排放量的因素主 要涉及以下五个方面:
第一,钢铁工业一切生产活动均服务于钢铁生产,粗钢产量会直接影响钢铁 工业CO2排放量。
第二,世界各国城市化进程需要钢铁工业的支持,城市化意味着建筑、汽车、 家电等制造行业以及基础设施建设的需求增加。钢铁是建筑中最重要的材料,也 是汽车生产中的主要材料之一,还被广泛运用到家电或其他装备制造行业,基础 设施的投资以及建设会拉动钢铁的需求,从而影响钢铁工业整体CO2排放量。
第三,全球化趋势的持续深入为世界各国钢铁工业贸易开放的进一步扩大 提供了可能。钢铁工业贸易开放度的扩大使世界钢铁工业生产要素得到充分利 用,优化资源配置,改善各国钢铁工业结构,提高绿色生产技术水平,减少世界 钢铁工业整体CO2排放量。
第四,环境库兹涅茨曲线假设经济增长与环境污染存在“倒U”形关系。一个 国家经济发展处在低水平时,人均GDP提高会导致环境污染的增加,当人均GDP 提高到一定水平时,环境污染水平达到顶峰,随着人均GDP的进一步增加,环 境污染会得到改善。
第五,金融发展有利于钢铁工业获取资金用于节能减排,金融发展在一定程 度上对钢铁工业CO2排放量有负向影响。
现搜集了2000年至2019年中国、印度、日本、美国、俄罗斯和世界钢铁工 业CO2排放量以及世界粗钢产量,2015年至2019年中国、印度、日本、美国和 俄罗斯的吨粗钢CO2排放量、高炉煤气消耗热量和电弧炉炼钢占比。见附件1“数 据推断填空”。
• 单位粗钢CO2排放量是评价一国钢铁低碳发展的重要指标,其数值越小 代表每一单位粗钢所排放的CO2量越小。
• 高炉煤气是在高炉炼铁中所产生的一种副产品,属于可燃气体,可用于 加热热轧的钢锭、预热钢水包等。高炉煤气主要成分为一氧化碳、二氧化碳、氮 气、氢气和甲烷等。高炉煤气消耗热量包括能源转型消耗、行业自用消耗、损失 以及统计误差,可作为衡量一国低碳发展的指标。
• 相比于传统“高炉-转炉”长流程炼钢工艺,电弧炉炼钢所产生的CO2排放 量仅为前者的1/3.电弧炉炼钢可有效减少世界钢铁工业CO2排放量,是打破长 流程炼钢的依赖、适应世界钢铁工业低碳发展新格局的重要手段。
本题旨在通过解决如下4个问题,明确自1990年以来的钢铁工业CO2排放 量的趋势和我国在世界钢铁工业低碳转型中的贡献率,定量表征粗钢产量 (PROUD,单位:千吨)、城市人口(URBAN)、钢铁工业贸易开放度(COPEN) 计算的相关指标(单位:千吨)、人均GDP(RGDP,2010年不变价美元)和 金融发展指数(FD,取值0到1,取值越大,表示金融发展程度越好)对钢铁工 业CO2排放量的影响,为中国钢铁工业高质量发展推荐最优路径。
1 .确定世界钢铁工业CO2排放量与中国、印度、日本、美国、俄罗斯钢铁 工业CO2排放量间的定量关系,补齐附件文件“数据推断填空”中标黄的缺失数 据,并构建数学模型说明所填数据的依据。
可以使用多元线性回归方法
多元线性回归是统计学和机器学习中一种常用的预测建模方法。它建立在简单线性回归的基础上,允许同时考虑多个自变量对因变量的影响。以下是多元线性回归的要点总结:
模型表示:多元线性回归模型用数学表达式表示为:Y = β₀ + β₁X₁ + β₂X₂ + ... + βᵣXᵣ + ε其中,Y是因变量(要预测的目标变量),X₁, X₂, ..., Xᵣ是自变量(影响因变量的特征),β₀, β₁, β₂, ..., βᵣ是回归系数,表示自变量对因变量的影响程度,ε是误差项,代表未被考虑的其他因素对因变量的影响以及模型的不确定性。
回归系数:回归系数 βᵢ 衡量了每个自变量 Xᵢ对因变量 \(Y\) 的影响。系数的符号表明影响的方向(正相关或负相关),而系数的大小表示影响的强度。回归模型的目标是找到最优的回归系数,使得预测值和真实值之间的误差最小(通常使用最小二乘法来实现)。
模型假设:多元线性回归依赖于一些假设,包括线性关系、误差项的正态分布、自变量之间的独立性和误差项的同方差性。违背这些假设可能导致模型不准确。
拟合优度:拟合优度(R-squared)是用来评估模型对数据的拟合程度。它表示因变量变异中能被自变量解释的比例。R-squared的取值范围在0到1之间,越接近1表示模型拟合得越好,越接近0表示模型拟合较差。
模型评估:为了评估模型的性能,可以使用各种指标,如均方误差(Mean Squared Error, MSE)、均方根误差(Root Mean Squared Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)等。
特征工程:在构建多元线性回归模型时,选择合适的自变量对模型性能至关重要。特征工程涉及选择有意义的特征、处理缺失值、处理异常值、进行数据转换等操作。
预测和推断:多元线性回归模型可以用于预测未来的结果,也可以用于推断变量之间的关系。预测是通过输入新的自变量值来估计因变量值,而推断则是对回归系数进行显著性检验,以确定自变量是否对因变量有显著影响。
总的来说,多元线性回归是一种强大的建模技术,可以用于探索变量之间的关系、进行预测和推断分析。然而,建立合理的模型需要注意数据的质量、特征工程的选择以及对模型假设的验证与修正。
% 输入数据
year = [2000:2019]'; % 年份
china_CO2 = [2.52 2.68 2.74 3.27 3.76 4.89 5.64 6.66 7.19 8.43 9.45 10.52 11.01 11.86 12.40 11.86 11.65 11.35 12.62 12.89]'; % 中国钢铁工业CO2排放量
india_CO2 = [0.70 0.67 0.82 0.80 0.82 0.86 1.00 1.11 1.14 1.39 1.56 1.83 1.85 2.00 2.25 2.31 2.45 2.61 2.93 2.92]'; % 印度钢铁工业CO2排放量
japan_CO2 = [0.78 0.76 0.78 0.81 0.81 0.85 0.86 0.89 0.83 0.76 0.88 0.90 0.89 0.89 0.87 0.83 0.81 0.83 0.81 0.79]'; % 日本钢铁工业CO2排放量
usa_CO2 = [0.91 0.76 0.53 0.58 0.68 0.50 0.54 0.51 0.52 0.33 0.49 0.51 0.48 0.49 0.49 0.47 0.47 0.51 0.48 0.48]'; % 美国钢铁工业CO2排放量
russia_CO2 = [0.75 0.73 0.75 0.71 0.73 0.83 0.71 0.92 0.86 0.85 0.91 1.01 1.38 1.34 1.44 1.46 1.48 1.47 1.54 1.70]'; % 俄罗斯钢铁工业CO2排放量
world_CO2 = [8.75 8.74 8.56 9.10 10.10 10.83 11.65 12.84 13.57 13.93 15.57 17.40 17.94 18.76 19.86 19.03 18.75 18.84 20.39 21.12]'; % 世界钢铁工业CO2排放量
% 构建设计矩阵X
X = [china_CO2, india_CO2, japan_CO2, usa_CO2, russia_CO2];
% 使用多元线性回归模型拟合数据
mdl = fitlm(X, world_CO2);2. 结合前面的研究,综合考虑世界粗钢产量、中国、印度、日本、美国、 俄罗斯粗钢产量,以及粗钢产量和钢铁工业CO2排放量间一一对应的数据关系, 构建数学模型确定中国、印度、日本、美国和俄罗斯在2000年至2019年的粗钢 产量,并自行验证求解结果的准确性。
3 . 根据附件文件“影响因素数据”,确定中国、印度、日本、美国和俄罗 斯的钢铁工业CO2排放量计算模型,并实证分析计算模型的灵敏度和鲁棒性。
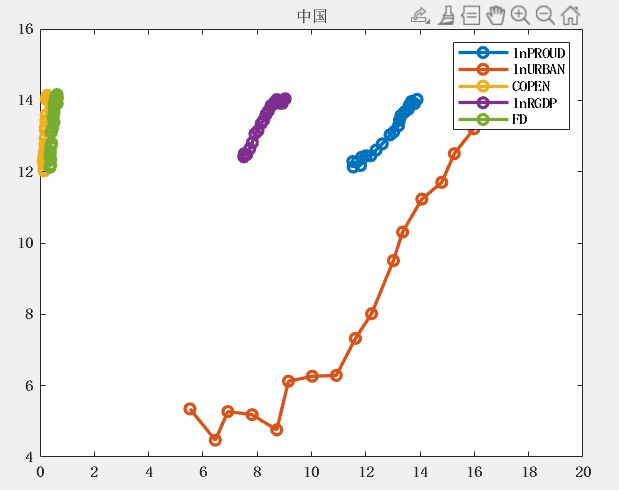
可视化如下:
4 .结合上面的三个问题研究结果,构建中国钢铁工业CO2排放量最低的优 化模型,以模型计算结果数据或前面的研究结果数据为依据,制定中国钢铁工业 低碳转型与高质量发展的优化路径。