Leetcode376. 摆动序列
Every day a Leetcode
题目来源:376. 摆动序列
解法1:动态规划
约定:
- 某个序列被称为「上升摆动序列」,当且仅当该序列是摆动序列,且最后一个元素呈上升趋势。
- 某个序列被称为「下降摆动序列」,当且仅当该序列是摆动序列,且最后一个元素呈下降趋势。
- 特别地,对于长度为 1 的序列,它既是「上升摆动序列」,也是「下降摆动序列」。
- 序列中的某个元素被称为「峰」,当且仅当该元素两侧的相邻元素均小于它。
- 序列中的某个元素被称为「谷」,当且仅当该元素两侧的相邻元素均大于它。
- 特别地,对于位于序列两端的元素,只有一侧的相邻元素小于或大于它,我们也称其为「峰」或「谷」。
- 对于序列中既非「峰」也非「谷」的元素,我们称其为「过渡元素」。
状态数组:
- up[i]:表示以前 i 个元素中的某一个为结尾的最长的「上升摆动序列」的长度。
- down[i]:表示以前 i 个元素中的某一个为结尾的最长的「下降摆动序列」的长度。
最终的状态转移方程为:
最终的答案即为 up[n−1] 和 down[n−1] 中的较大值,其中 n 是序列的长度。
代码:
/*
* @lc app=leetcode.cn id=376 lang=cpp
*
* [376] 摆动序列
*/
// @lc code=start
class Solution
{
public:
int wiggleMaxLength(vector<int> &nums)
{
// 特判
if (nums.size() <= 1)
return nums.size();
int n = nums.size();
// 状态数组
// up[i]:表示以前i个元素中的某一个为结尾的最长的「上升摆动序列」的长度
vector<int> up(n + 1, 0);
// down[i]:表示以前i个元素中的某一个为结尾的最长的「下降摆动序列」的长度
vector<int> down(n + 1, 0);
// 初始化
// 对于长度为1的序列,它既是「上升摆动序列」,也是「下降摆动序列」
up[1] = down[1] = 1;
// 状态转移
for (int i = 2; i <= n; i++)
{
if (nums[i - 1] > nums[i - 2])
{
up[i] = max(up[i - 1], down[i - 1] + 1);
down[i] = down[i - 1];
}
else if (nums[i - 1] < nums[i - 2])
{
up[i] = up[i - 1];
down[i] = max(up[i - 1] + 1, down[i - 1]);
}
else
{
up[i] = up[i - 1];
down[i] = down[i - 1];
}
}
return max(up[n], down[n]);
}
};
// @lc code=end
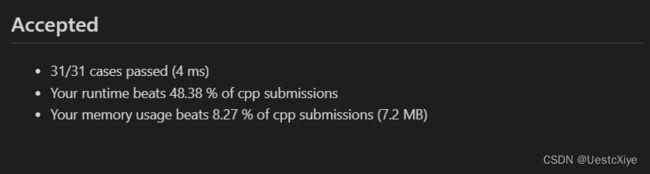
结果:
复杂度分析:
时间复杂度:O(n),其中 n 是序列的长度。我们只需要遍历该序列一次。
空间复杂度:O(n),其中 n 是序列的长度。我们需要开辟两个长度为 n 的数组。
空间优化
代码:
/*
* @lc app=leetcode.cn id=376 lang=cpp
*
* [376] 摆动序列
*/
// @lc code=start
// 动态规划
// class Solution
// {
// public:
// int wiggleMaxLength(vector &nums)
// {
// // 特判
// if (nums.size() <= 1)
// return nums.size();
// int n = nums.size();
// // 状态数组
// // up[i]:表示以前i个元素中的某一个为结尾的最长的「上升摆动序列」的长度
// vector up(n + 1, 0);
// // down[i]:表示以前i个元素中的某一个为结尾的最长的「下降摆动序列」的长度
// vector down(n + 1, 0);
// // 初始化
// // 对于长度为1的序列,它既是「上升摆动序列」,也是「下降摆动序列」
// up[1] = down[1] = 1;
// // 状态转移
// for (int i = 2; i <= n; i++)
// {
// if (nums[i - 1] > nums[i - 2])
// {
// up[i] = max(up[i - 1], down[i - 1] + 1);
// down[i] = down[i - 1];
// }
// else if (nums[i - 1] < nums[i - 2])
// {
// up[i] = up[i - 1];
// down[i] = max(up[i - 1] + 1, down[i - 1]);
// }
// else
// {
// up[i] = up[i - 1];
// down[i] = down[i - 1];
// }
// }
// return max(up[n], down[n]);
// }
// };
// 动态规划-空间优化
class Solution
{
public:
int wiggleMaxLength(vector<int> &nums)
{
// 特判
if (nums.size() <= 1)
return nums.size();
int n = nums.size();
int up = 1, down = 1;
// 状态转移
for (int i = 1; i < n; i++)
{
if (nums[i] > nums[i - 1])
up = max(up, down + 1);
else if (nums[i] < nums[i - 1])
down = max(down, up + 1);
}
return max(up, down);
}
};
// @lc code=end
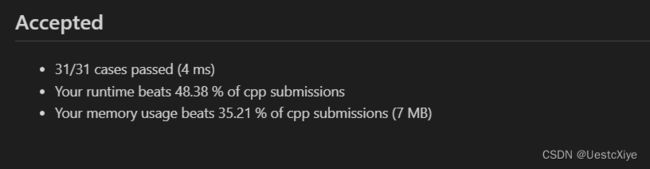
结果:
解法2:贪心
观察这个序列可以发现,我们不断地交错选择「峰」与「谷」,可以使得该序列尽可能长。证明非常简单:如果我们选择了一个「过渡元素」,那么在原序列中,这个「过渡元素」的两侧有一个「峰」和一个「谷」。不失一般性,我们假设在原序列中的出现顺序为「峰」「过渡元素」「谷」。如果「过渡元素」在选择的序列中小于其两侧的元素,那么「谷」一定没有在选择的序列中出现,我们可以将「过渡元素」替换成「谷」;同理,如果「过渡元素」在选择的序列中大于其两侧的元素,那么「峰」一定没有在选择的序列中出现,我们可以将「过渡元素」替换成「峰」。这样一来,我们总可以将任意满足要求的序列中的所有「过渡元素」替换成「峰」或「谷」。并且由于我们不断地交错选择「峰」与「谷」的方法就可以满足要求,因此这种选择方法就一定可以达到可选元素数量的最大值。
这样,我们只需要统计该序列中「峰」与「谷」的数量即可(注意序列两端的数也是「峰」或「谷」),但需要注意处理相邻的相同元素。
在实际代码中,我们记录当前序列的上升下降趋势。每次加入一个新元素时,用新的上升下降趋势与之前对比,如果出现了「峰」或「谷」,答案加一,并更新当前序列的上升下降趋势。
代码:
/*
* @lc app=leetcode.cn id=376 lang=cpp
*
* [376] 摆动序列
*/
// @lc code=start
// 动态规划
// class Solution
// {
// public:
// int wiggleMaxLength(vector &nums)
// {
// // 特判
// if (nums.size() <= 1)
// return nums.size();
// int n = nums.size();
// // 状态数组
// // up[i]:表示以前i个元素中的某一个为结尾的最长的「上升摆动序列」的长度
// vector up(n + 1, 0);
// // down[i]:表示以前i个元素中的某一个为结尾的最长的「下降摆动序列」的长度
// vector down(n + 1, 0);
// // 初始化
// // 对于长度为1的序列,它既是「上升摆动序列」,也是「下降摆动序列」
// up[1] = down[1] = 1;
// // 状态转移
// for (int i = 2; i <= n; i++)
// {
// if (nums[i - 1] > nums[i - 2])
// {
// up[i] = max(up[i - 1], down[i - 1] + 1);
// down[i] = down[i - 1];
// }
// else if (nums[i - 1] < nums[i - 2])
// {
// up[i] = up[i - 1];
// down[i] = max(up[i - 1] + 1, down[i - 1]);
// }
// else
// {
// up[i] = up[i - 1];
// down[i] = down[i - 1];
// }
// }
// return max(up[n], down[n]);
// }
// };
// 动态规划-空间优化
// class Solution
// {
// public:
// int wiggleMaxLength(vector &nums)
// {
// // 特判
// if (nums.size() <= 1)
// return nums.size();
// int n = nums.size();
// int up = 1, down = 1;
// // 状态转移
// for (int i = 1; i < n; i++)
// {
// if (nums[i] > nums[i - 1])
// up = max(up, down + 1);
// else if (nums[i] < nums[i - 1])
// down = max(down, up + 1);
// }
// return max(up, down);
// }
// };
// 贪心
class Solution
{
public:
int wiggleMaxLength(vector<int> &nums)
{
// 特判
if (nums.size() <= 1)
return nums.size();
int n = nums.size();
int preDiff = nums[1] - nums[0];
int ans = preDiff != 0 ? 2 : 1;
for (int i = 2; i < n; i++)
{
int diff = nums[i] - nums[i - 1];
if ((diff > 0 && preDiff <= 0) || (diff < 0 && preDiff >= 0))
{
ans++;
preDiff = diff;
}
}
return ans;
}
};
// @lc code=end
结果:
复杂度分析:
时间复杂度:O(n),其中 n 是序列的长度。我们只需要遍历该序列一次。
空间复杂度:O(1)。我们只需要常数空间来存放若干变量。
第二种贪心思路:统计变化次数
代码:
// 贪心2
class Solution
{
public:
int wiggleMaxLength(vector<int> &nums)
{
// 特判
if (nums.size() <= 1)
return nums.size();
int n = nums.size();
int direction = 0; //-1表示下降,1表示上升
int count = 0; // 变化次数
for (int i = 1; i < n; i++)
{
if (nums[i] > nums[i - 1])
{
if (direction != 1)
{
direction = 1;
count++;
}
}
else if (nums[i] < nums[i - 1])
{
if (direction != -1)
{
direction = -1;
count++;
}
}
}
// 因为统计的是变化的次数,最终的结果是序列的长度,所以需要+1
return count + 1;
}
};
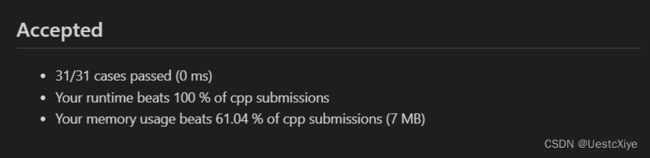
结果:
复杂度分析:
时间复杂度:O(n),其中 n 是序列的长度。我们只需要遍历该序列一次。
空间复杂度:O(1)。我们只需要常数空间来存放若干变量。