Leetcode646. 最长数对链

Every day a Leetcode

题目来源：646. 最长数对链

解法1：动态规划

定义 dp[i] 为以 pairs[i] 为结尾的最长数对链的长度。

初始化时，dp 数组需要全部赋值为 1。

计算 dp[i] 时，可以先找出所有的满足 pairs[i][0]>pairs[j][1] 的 j，并求出最大的 dp[j]，dp[i] 的值即可赋为这个最大值加一。

状态转移方程：dp[i] = max(dp[i], dp[j] + 1)

这种动态规划的思路要求计算 dp[i] 时，所有潜在的 dp[j] 已经计算完成，可以先将 pairs 数组进行排序来满足这一要求。

代码：

/*
 * @lc app=leetcode.cn id=646 lang=cpp
 *
 * [646] 最长数对链
 */

// @lc code=start
class Solution
{
public:
    int findLongestChain(vector<vector<int>> &pairs)
    {
        // 特判
        if (pairs.empty())
            return 0;
        int n = pairs.size();
        // 状态数组，并初始化
        vector<int> dp(n + 1, 1);
        // dp[i]: 为 pairs[i] 结尾的最长数对链的长度
        sort(pairs.begin(), pairs.end());
        //  状态转移
        for (int i = 1; i <= n; i++)
            for (int j = 1; j < i; j++)
                if (pairs[j - 1][1] < pairs[i - 1][0])
                    dp[i] = max(dp[i], dp[j] + 1);
        return dp[n];
    }
};
// @lc code=end

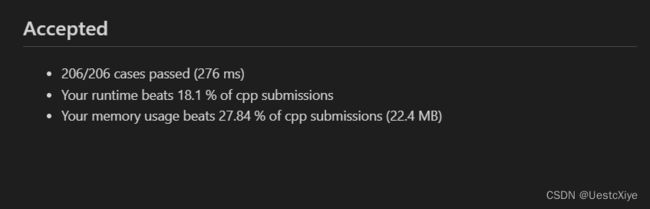
结果：

复杂度分析：

时间复杂度：O(n²)，其中 n 为 pairs 数组的长度。排序的时间复杂度为 O(nlogn)，两层 for 循环的时间复杂度为 O(n²)。

空间复杂度：O(n)，dp 数组的空间复杂度为 O(n)。

解法2：最长递增子序列

方法一实际上是「300. 最长递增子序列」的动态规划解法，这个解法可以改造为贪心 + 二分查找的形式。

用一个数组 arr 来记录当前最优情况，arr[i] 就表示长度为 i+1 的数对链的末尾可以取得的最小值，遇到一个新数对时，先用二分查找得到这个数对可以放置的位置，再更新 arr。

代码：

/*
 * @lc app=leetcode.cn id=646 lang=cpp
 *
 * [646] 最长数对链
 */

// @lc code=start

// 动态规划

// class Solution
// {
// public:
//     int findLongestChain(vector> &pairs)
//     {
//         // 特判
//         if (pairs.empty())
//             return 0;
//         int n = pairs.size();
//         // 状态数组，并初始化
//         vector dp(n + 1, 1);
//         // dp[i]: 为 pairs[i] 结尾的最长数对链的长度
//         sort(pairs.begin(), pairs.end());
//         //  状态转移
//         for (int i = 1; i <= n; i++)
//             for (int j = 1; j < i; j++)
//                 if (pairs[j - 1][1] < pairs[i - 1][0])
//                     dp[i] = max(dp[i], dp[j] + 1);
//         return dp[n];
//     }
// };

// 贪心 + 二分查找

class Solution
{
public:
    int findLongestChain(vector<vector<int>> &pairs)
    {
        sort(pairs.begin(), pairs.end());
        vector<int> dp;
        for (auto &pair : pairs)
        {
            int x = pair[0], y = pair[1];
            if (dp.empty() || dp.back() < x)
                dp.push_back(y);
            else
            {
                auto iter = lower_bound(dp.begin(), dp.end(), x);
                *iter = min(*iter, y);
            }
        }
        return dp.size();
    }
};
// @lc code=end

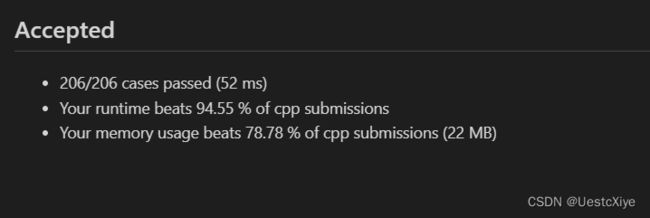
结果：

复杂度分析：

时间复杂度：O(nlog⁡n)，其中 n 为 pairs 的长度。排序的时间复杂度为 O(nlogn)，二分查找的时间复杂度为 O(nlogn)，二分的次数为 O(n)。

空间复杂度：O(n)，数组 arr 的长度最多为 O(n)。

解法3：贪心

要挑选最长数对链的第一个数对时，最优的选择是挑选第二个数字最小的，这样能给挑选后续的数对留下更多的空间。

挑完第一个数对后，要挑第二个数对时，也是按照相同的思路，是在剩下的数对中，第一个数字满足题意的条件下，挑选第二个数字最小的。

按照这样的思路，可以先将输入按照第二个数字排序，然后不停地判断第一个数字是否能满足大于前一个数对的第二个数字即可。

代码：

class Solution
{
private:
    // 排序函数
    static bool cmp(const vector<int> &a, const vector<int> &b)
    {
        return a[1] < b[1];
    }

public:
    int findLongestChain(vector<vector<int>> &pairs)
    {
        int cur = INT_MIN, res = 0;
        sort(pairs.begin(), pairs.end(), cmp);
        for (auto &pair : pairs)
        {
            int x = pair[0], y = pair[1];
            if (cur < x)
            {
                cur = y;
                res++;
            }
        }
        return res;
    }
};

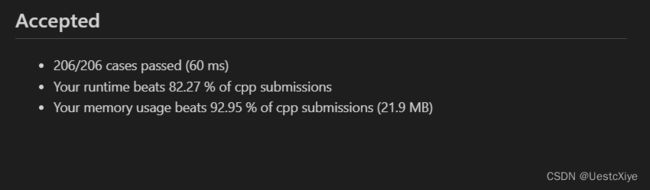
结果：

复杂度分析：

时间复杂度：O(nlog⁡n)，其中 n 为 pairs 的长度。排序的时间复杂度为 O(nlogn)。

空间复杂度：O(log⁡n)，为排序的空间复杂度。