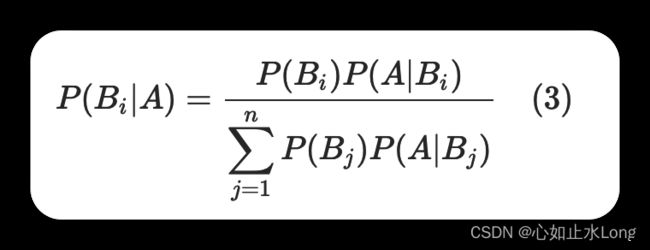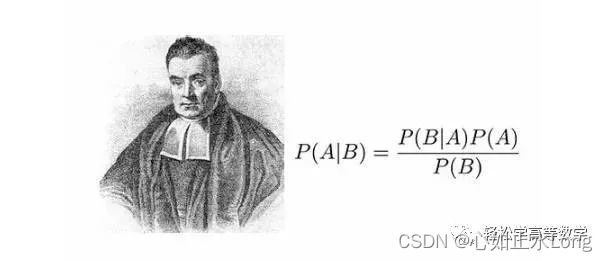【概率论与数理统计】第一节课——随机事件与概率(3/3)
随机事件与概率
贝叶斯公式
概念
与全概率公式解决的问题相反,贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因(即大事件A已经发生的条件下,分割中的小事件Bi在A发生的条件下的概率),设B1,B2,...是样本空间S的一个划分,则对任一事件A(P(A)>0),有
上式即为贝叶斯公式(Bayes formula),Bi 常被视为导致试验结果A发生的“原因”,P(Bi)(i=1,2,...)表示各种原因发生的可能性大小,故称先验概率(权重);P(Bi|A)(i=1,2...)则反映当试验产生了结果A之后,再对各种原因概率的新认识,故称后验概率。
在运用贝叶斯公式时,一般已知和未知条件为:- B的多种情况中到底哪种情况发生了是未知的,但是每种情况发生的概率已知,即P(Bj);
- 事件A是已经发生的确定事实,且每种B发生条件下A发生的概率已知,即P(A|Bj);
- P(A)未知,需要使用全概率公式计算得到;
- 求解的目标是用B的某种情况Bi的无条件概率求其在A发生的条件下的有条件概率P(Bi|A)
手写笔记
贝叶斯公式最神奇之处在于将条件概率中的因和果调换了位置,可以用下面这个公式来进行表示
P(B|A) = P(因|果) = P(因)P(果|因)/P(果)
习题1: 设某公路经过的货车与客车的数量之比为1:2,货车中途停车修车的概率为0.02,客车为0.01,今有一辆汽车中途停车修理,则该车是货车的概率是多少?

原本汽车中途停车维修的概率应该与车的数量成正比,即在只考虑车的数量时,停下来的车为货车的概率为P(A1),即1/3;
但是当我们进一步观察,加入更多的信息(每种类型的车的停车维修的概率)后,判断停下来的车为货车的概率增加到了1/2,也就是说B的发生使得A1(观察到货车停下来维修)发生的概率变大了。(货车的数量虽然少,但是经过长期观察,货车出故障的概率是客车的2倍<获得了新的信息>,因此货车停在路边维修的概率就增加了)
习题2: 装有10件某产品(乒乓球)(其中一等品5件,二等品3件,三等品2件)的箱子中丢失一件产品,但不知是几等品,今从箱中任取2件产品,结果都是一等品,则丢失的也是一等品的概率为?

由于我们不知道丢失了哪种球,最直接的猜测就是丢每种球的概率与球的数量成正比。即,丢的球是一等品的概率为1/2 = P(A1)。
但是为了更加准确的推测到底丢了什么球,只能通过一些可行的方法,获得更多的信息。这里采用了"任取两个球出来"这种试验方法,然后根据试验结果得到了更加准确的结果3/8,也就是说,这一结果降低了我们前面直接根据球的数量预测出的概率。(因为任取两个都是一等品,说明剩下的球中,取到一等品的概率很大,因此丢的可能性就变小了)
来源:http://www.cnblogs.com/Belter/p/5923828.html
现在应该对贝叶斯公式有个人大致了解了,现在借用冯春明老师的轻松学概率论,给各位朋友们更好的理解一下贝叶斯公式及她的应用
&nesp; 贝叶斯定理实际上就是条件概率公式:设A,B是两个事件,且P(B)>0,则在事件B发生的条件下,事件A发生的条件概率(conditional probability)为:
P(A|B)=P(AB)/P(B)P(A)是A的先验概率,之所以成为先验是因为它不考虑任何B的因素,P(B)同理;
P(A|B)实在B发生时A发生的条件概率,称坐A的后验概率,P(B|A)同理。
贝叶斯定理通俗地讲,就是当你不能确定某一个事件发生的概率时,你可以依靠与该时间本质属性相关的事件发生的概率去推测该事件发生的概率
全概公式与贝叶斯公式解析
直接上例题
例题:一所学校里面有 60%的男生,40% 的女生。男生总是穿长裤,女生则一半穿长裤一半穿裙子。
1、迎面走来一个学生,问他(她)穿长裤的概率是多大;
2、迎面走来一个穿长裤的学生(很不幸的是你高度近视,你只看得见他(她)穿的是否长裤,而无法确定他(她)的性别),你能够推断出他(她)是男生的概率是多大吗?
总之,全概公式是由多个因推果 ,是正向概率,而贝叶斯公式是由果推因,是逆向概率.在贝叶斯公式中,通常称 P(B1),P(B2),...P(B1),P(B2),...为先验概率,而称 P(B1|A),P(B2|A),...P(B1|A),P(B2|A),... 为后验概率。因而,贝叶斯公式实际上是计算后验概率的公式。
习题3
设n 件产品中有 m 件不合格品,从中任取两件,已知两件中有一件是合格品,求另一件也是合格品的概率.

习题4
口袋中有 1 个白球,1 个黑球.从中任取 1 个,若取出白球,则试验停止;若取出黑球,则把取出的黑球放回的同时,再加入 1 个黑球,如此下去,直到取出的是白球为止,试求下列事件的概率.
(1)取到第 n 次,试验没有结束;
(2)取到第 n 次,试验恰好结束.

这里有一个学姐记的例题,我也放这里了
例题5:
钥匙掉了,掉在宿舍里、掉在教室里、掉在路上的概率分别是 50%、30%和 20%,而掉在上述三处地方被找到的概率分别是 0.8、0.3 和 0.1.试求找到钥匙的概率.

例题6:
两台车床加工同样的零件,第一台出现不合格品的概率是 0.03,第二台出现不合格品的概率是 0.06,加工出来的零件放在一起,并且已知第一台加工的零件比第二台加工的零件多一倍.
(1)求任取一个零件是合格品的概率;
(2)如果取出的零件是不合格品,求它是由第二台车床加工的概率

小故事(还没理解贝叶斯公式的看看这个故事)
给大家看一张图和一篇文章啊,有点意思的

今天实习生小天兴冲冲地跑到超模君面前,问道:我今天遇到了一个老朋友,你猜猜 是男的还是女的,嘿嘿 ?
说完后小天故意抛出一个邪魅的笑容
作为数据建模界的老司机,超模君静下心来思考:
从概率论的角度来看,睿智的超模君,应该怎么猜,猜中的概率才大些呢?
如果只是简单的 P(老朋友=男性)=P(老朋友=女性)=50% ,那这个回答没啥技术含量,于是超模君问小天:有没有更多的提示? (贝叶斯的核心思想就是获取更多信息)
小天想了一下说:我们是在 Gucci 店里购物时遇见的哦!
听完这句话,超模君推测:是小天的老朋友,同时,还会逛Gucci的人,那么这个人为女性的概率为: P(老朋友=女性 | 老朋友会逛 Gucci ) = 80%。
嗯嗯,超模君基本上可以确定这个老朋友应该是女性了。
然而结果并不是,最后,小天说的老朋友居然是他的男神 刘强西 。。。
超模君居然猜错了,╮(╯▽╰)╭,而刘强西原来还逛Gucci?嚯嚯嚯。。
也罢也罢,这也让超模君知道今天该教大家什么了,那就是综合情报判断概率神器: 贝叶斯公式(Bayes’ Rule)
首先,我们看看它长得什么样子:
P(A|B)=P(AB)/P(B)就是这么一条非常基本的定律却在 数学、金融、博弈论、生命基因 中有非常重要的作用。
更重要的是,在现实生活中, 我们其实会常常 直觉无意识 地使用贝叶斯公式!
比如在文章小故事开头“ 超模君判断 小天老友性别事件” 便是综合已知情报和概率估算的初级应用。
也就在今天,京西旅馆发生了大事,
老板刘强西此时 面如死灰 的坐在旅馆前台。
原来是某医院近期在做 HIV(艾滋病)免费测纸派发活动 ,刘强西听到免费后,两眼放光,直接带了一些测纸回到旅馆。
回到旅馆后,刘强西开始给自己开始做检测,心想: 我健康着呢!
是故事就会反转,测试完后,刘强西面如死灰坐在旅馆强台。。。
小天来到旅馆后,了解到刘强西的事情,心中大喊: 我去,我要赶紧离职!
不过转念一想,这老板对我也不错,况且又不会传染!
可是日常生活健康的刘强西,怎么就染上这个了呢?
于是小天开始上网翻阅各种资料,检索各种资料 ,对HIV有个新的了解。
小天发现:
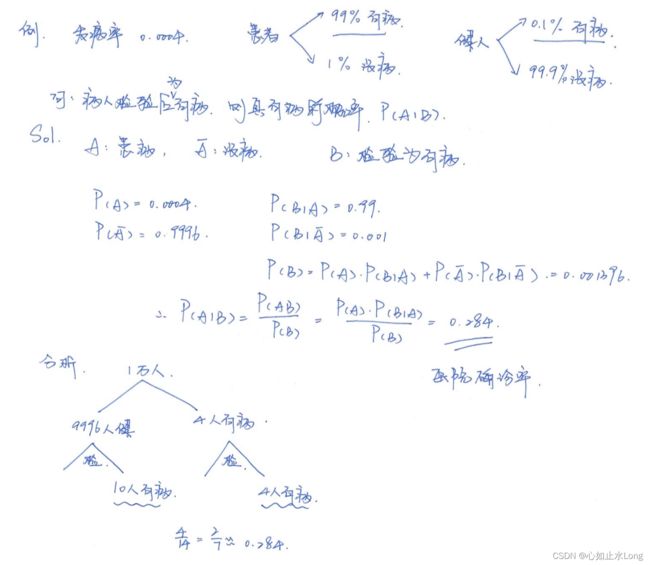
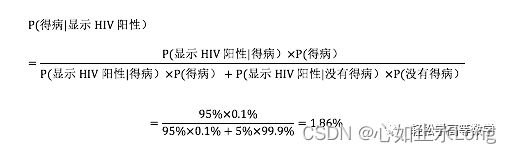
HIV 这种的发病率是0.001,即1000人会有1个人得病,有
P(得病) = 0.1%
而免费活动赠送的测试试纸的准确率为 95% 。
换句话说,① 如果真的得了艾滋病,该试纸有95%的检测出HIV阳性;② 如果没有得病,该试纸也有5%的出错率,错误的显示你有HIV阳性。
贝叶斯曾说过 :在 没有做测纸试验之前,我们预计的发病率, P(得病) = 0.1%, 这个呢,就叫作 “先验概率” 。
而在我们做完测纸 表示阳性后,那么要计算的就是 P(得病|显示HIV阳性)=95%,这个呢, 则称为 “后验概率”。
小天 拿着找到的资料,来到刘强西面前。扒拉,一把计算结果放在桌上:Boss,你看!
强西不耐烦:走开,别来烦我!
小天:老板,你被骗了!
刘强西一听,两眼放光:纳尼?!!!
小天:老板,哪怕试纸测出了你是HIV阳性,你真的得病的概率也 只有1.86% ?
你想 这是为什么吗?嘻嘻嘻
你这种情况有可能是假阳性,根据我 情报小助手的推算 ,得病的机率 只从0.1%提高到了1.86%而已 。
刘强西听到后,才1.86%的可能,一下子抓住小天:你说真的吗?我TM还没死,我还能活着。
小天,你是我见过最聪明的实习生。
也就在此时,社区王大妈突然来旅馆:强西,还有小天,有个居委会有个新通知,你们注意点,你们也别嫌我唠叨。最近有个“ 莆田”医院 在发HIV测纸,你们应该没用吧。
们尽作伤天害理的事,拿了一堆 假的测纸免费 发给大家,好多人都被骗了。这些医院为了赚钱还TM什么事都做的出来。
你们两个当心点,不要被骗了!先不和你们闲聊,还有30家要去通知呢!
王大妈一个人念叨完后,给小天和刘强西只留下 壮硕的背影 。
夕阳下的王大妈,如同圣母般关怀着京西旅馆!
例题6:
已知男人中有 5%是色盲患者,女人中有 0.25%是色盲患者,今从男女比例为 22:21 的人群中随机地挑选一人,发现恰好是色盲患者,问此人是男性的概率是多少?

例题7:
口袋中 a 个白球,b 个黑球和 n 个红球,现从中一个一个不返回地取球.试证白球比黑球出现得早的概率为 a/(a + b),与 n 无关.

好了,看了几道例题后我们再把贝叶斯公式和全概念公式给一下,加深一下印象

例题8:
某学生无意将自己的钥匙丢掉了,他记得钥匙丢在教室里,宿舍里,操场上,道路上的概率分别为0.3,0.25,0.35和0.1.如果钥匙丢在教室里,能被找到的概率为0.45;如果钥匙丢在宿舍里,能被找到的概率为0.67;如果钥匙丢在操场上,能被找到的概率为0.27;如果钥匙丢在道路上, 能被找到的概率为0.12.
(1)求该学生找到钥匙的概率;
(2)如果该学生找到了钥匙,求他在操场上找到的概率。