《算法系列》之栈
简介
栈是一种基础的数据结构,用到栈的部分题还是很难的。代码书写难度还好,主要思维难度上,大家可能并不知道需要用到栈。尤其是用到单调栈的情况,很难把题抽象为用栈解决。这时只能多加练习了,练多了我们就会发现,遇到数制转换,括号匹配,表达式求值等经典题型时,我们就可以考虑用栈去解决。
理论基础
栈是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。栈以底层容器为基础,对外提供统一的操作接口,底层容器是可插拔的,即可切换。 栈的底层容器,可以是数组、链表、集合等。除了可以用多种底层容器实现以外,栈最大的特点就是:“先进后出,后进先出”,这个特征在解题时要尤其注意。

代码实现
顺序栈
/**
* 基于数组的顺序栈
*/
public class ArrayStack {
private String[] items; // 数组
private int count; // 栈中元素个数
private int n; // 栈的大小
// 初始化数组,申请一个大小为 n 的数组空间
public ArrayStack(int n) {
this.items = new String[n];
this.n = n;
this.count = 0;
}
/**
* 入栈
* 数组入栈的入口为数组尾部
* @param item :入栈数据元素
* @return:是否入栈成功
*/
public boolean push(String item) {
// 数组空间不够了,直接返回 false,入栈失败。
if (count == n) return false;
// 将 item 放到下标为 count 的位置
items[count] = item;
// 数组长度+1
++count;
// 入栈成功
return true;
}
/**
* 出栈
* @return:返回出栈元素
*/
public String pop() {
// 栈为空,则直接返回 null
if (count == 0) return null;
// 返回下标为 count-1 的数组元素
String tmp = items[count-1];
// 数组长度-1
--count;
// 返回出栈数据元素
return tmp;
}
}
链式栈
/**
* 基本链表实现栈,入栈、出栈、输出栈
*/
public class StackBasedLinkedList {
// 定义栈顶指针
private Node top = null;
// 定义栈结点
private static class Node {
// 栈结点数据域
private int data;
// 栈结点指针域
private Node next;
// 构造函数
public Node(int data, Node next) {
this.data = data;
this.next = next;
}
// get 获取数据域方法
public int getData() {
return data;
}
}
/**
* 入栈
* @param value:要入栈的数据元素
*/
public void push(int value) {
// 创建一个栈结点
Node newNode = new Node(value, null);
// 判断栈是否为空
if (top == null) {
// 如果栈为空,就将入栈的值作为栈的第一个元素
top = newNode;
} else {
// 否则插入到top栈结点前(所谓的就是单链表的头插法)
newNode.next = top;
top = newNode;
}
}
/**
* 出栈
* @return: -1 为栈中没有数据
*/
public int pop() {
// 如果栈的最顶层栈结点为null,栈为空
if (top == null) return -1;
// 否则执行出栈操作,现将栈顶结点的数据元素赋值给 Value
int value = top.data;
// 将 top 指针向下移动
top = top.next;
// 返回出栈的值
return value;
}
/**
* 输出栈中所有元素
*/
public void printAll() {
// 将栈顶指针赋值给p
Node p = top;
// 循环遍历栈(遍历单链表)
while (p != null) {
System.out.print(p.data + " ");
// 指向下一个结点
p = p.next;
}
System.out.println();
}
}
解题心得
- 涉及单调栈的题可能并不简单,需要多多练习与分析。
- 熟悉了解栈的基础特点,是解题的关键。
- 栈是一种线性表,经典解题法有数制转换,括号匹配,表达式求值等,遇到这些类型的题时,我们应该首先尝试用栈去解决。
- 在树的迭代法遍历中,栈有很大作用。
- 栈可以用多种基础容器实现,甚至可以用其它数据结构实现,比如用队列实现栈。
算法题目
20. 有效的括号

题目解析:如果是左括号就入栈,右括号就与栈顶比较。
代码如下:
/**
* 栈
*/
class Solution {
public boolean isValid(String s) {
Stack stack = new Stack();
for (int i = 0; i < s.length(); i++) {
char symbol = s.charAt(i);
if (symbol == '(' || symbol == '{' || symbol == '[') {
stack.push(symbol);
} else {
if (stack.isEmpty()) {
return false;
}
if (symbol == ')' && stack.pop() != '(') {
return false;
}
if (symbol == '}' && stack.pop() != '{') {
return false;
}
if (symbol == ']' && stack.pop() != '[') {
return false;
}
}
}
if (stack.isEmpty()) {
return true;
}
return false;
}
}
32. 最长有效括号

题目解析:从左往右扫描,栈内保存括号位置下标,最后做减法确定长度,用 max() 确定最长长度,类似于 “消消乐”。
代码如下:
/**
* 栈
*/
class Solution {
public int longestValidParentheses(String s) {
int maxans = 0;
Stack stack = new Stack<>();
stack.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else {
stack.pop();
if (stack.empty()) {
stack.push(i);
} else {
maxans = Math.max(maxans, i - stack.peek());
}
}
}
return maxans;
}
}
71. 简化路径

题目解析:用栈解决,先以“/”,做为分隔符,再用入栈出栈的方式简化路径。
代码如下:
/**
* 栈
*/
class Solution {
public String simplifyPath(String path) {
LinkedList stack = new LinkedList<>();
StringBuilder res = new StringBuilder();
// 以 “/” 为分隔符,分开path
String[] strings = path.split("/");
for (String s : strings) {
// 如果为空不做任何操作,去除多个///的情况
if (s.isEmpty() || s.equals(".")) {
continue;
}
// 去除上个父目录
if (s.equals("..")) {
if (!stack.isEmpty()) {
stack.pop();
}
} else {
stack.push(s);
}
}
// 用StringBuilder的拼接方式,可提高拼接速度,快过50%的提交
while (!stack.isEmpty()) {
res.append("/").append(stack.pollLast());
}
if (res.length() == 0) {
return "/";
}
return res.toString();
}
}
84. 柱状图中最大的矩形

题目解析:题意可理解为,在一维数组中对每一个数找到第一个比自己小的元素。这类“在一维数组中找第一个满足某种条件的数”的场景就是典型的单调栈场景。
代码如下:
/**
* 单调栈
*/
class Solution {
public int largestRectangleArea(int[] heights) {
int n = heights.length;
int[] left = new int[n];
int[] right = new int[n];
Deque mono_stack = new ArrayDeque();
for (int i = 0; i < n; ++i) {
while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
mono_stack.pop();
}
left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
mono_stack.push(i);
}
mono_stack.clear();
for (int i = n - 1; i >= 0; --i) {
while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
mono_stack.pop();
}
right[i] = (mono_stack.isEmpty() ? n : mono_stack.peek());
mono_stack.push(i);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
}
85. 最大矩形

题目解析:只需要计算每个柱状图中的最大面积,并找到全局最大值即可,用单调栈解决。
代码如下:
/**
* 单调栈
*/
class Solution {
public int maximalRectangle(char[][] matrix) {
int m = matrix.length;
if (m == 0) {
return 0;
}
int n = matrix[0].length;
int[][] left = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] == '1') {
left[i][j] = (j == 0 ? 0 : left[i][j - 1]) + 1;
}
}
}
int ret = 0;
for (int j = 0; j < n; j++) { // 对于每一列,使用基于柱状图的方法
int[] up = new int[m];
int[] down = new int[m];
Deque stack = new LinkedList();
for (int i = 0; i < m; i++) {
while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
stack.pop();
}
up[i] = stack.isEmpty() ? -1 : stack.peek();
stack.push(i);
}
stack.clear();
for (int i = m - 1; i >= 0; i--) {
while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
stack.pop();
}
down[i] = stack.isEmpty() ? m : stack.peek();
stack.push(i);
}
for (int i = 0; i < m; i++) {
int height = down[i] - up[i] - 1;
int area = height * left[i][j];
ret = Math.max(ret, area);
}
}
return ret;
}
}
150. 逆波兰表达式求值

题目解析:遇到数字就压入栈,如果是操作符就把栈顶两个数弹出计算,把结果再压入栈。
代码如下:
/**
* 栈
*/
class Solution {
public int evalRPN(String[] tokens) {
Stack stack = new Stack<>();
for (int i = 0; i < tokens.length; i++) {
int a, b;
switch (tokens[i]) {
case "+":
b = stack.pop();
a = stack.pop();
stack.push(a + b);
break;
case "-":
b = stack.pop();
a = stack.pop();
stack.push(a - b);
break;
case "*":
b = stack.pop();
a = stack.pop();
stack.push(a * b);
break;
case "/":
b = stack.pop();
a = stack.pop();
stack.push(a / b);
break;
default:
stack.push(new Integer(tokens[i]));
}
}
return stack.pop();
}
}
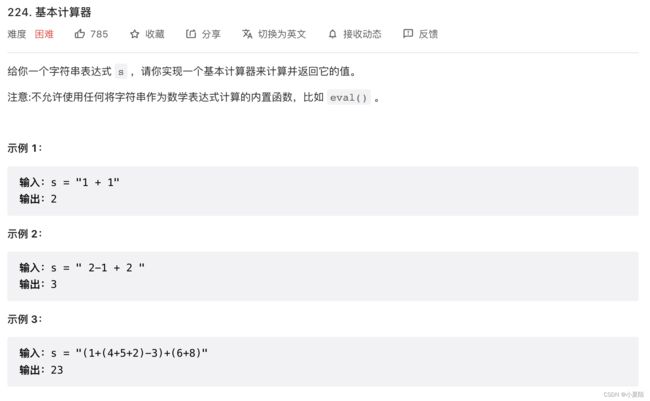
224. 基本计算器
/**
* 栈
*/
class Solution {
public int calculate(String s) {
Deque ops = new LinkedList();
ops.push(1);
int sign = 1;
int ret = 0;
int n = s.length();
int i = 0;
while (i < n) {
if (s.charAt(i) == ' ') {
i++;
} else if (s.charAt(i) == '+') {
sign = ops.peek();
i++;
} else if (s.charAt(i) == '-') {
sign = -ops.peek();
i++;
} else if (s.charAt(i) == '(') {
ops.push(sign);
i++;
} else if (s.charAt(i) == ')') {
ops.pop();
i++;
} else {
long num = 0;
while (i < n && Character.isDigit(s.charAt(i))) {
num = num * 10 + s.charAt(i) - '0';
i++;
}
ret += sign * num;
}
}
return ret;
}
}
227. 基本计算器 II
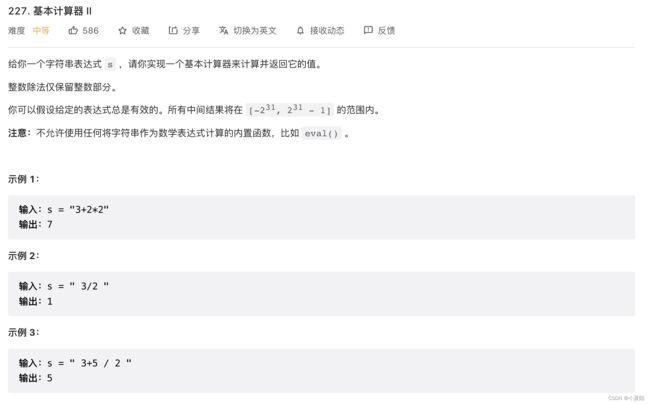
题目解析:用一个栈即可解决,用以存储各数值,减号存负值,乘除需计算后,再存入,最后累加栈内数值即可。
代码如下:
/**
* 栈
*/
class Solution {
public int calculate(String s) {
Deque stack = new LinkedList();
char preSign = '+';
int num = 0;
int n = s.length();
for (int i = 0; i < n; ++i) {
if (Character.isDigit(s.charAt(i))) {
num = num * 10 + s.charAt(i) - '0';
}
if (!Character.isDigit(s.charAt(i)) && s.charAt(i) != ' ' || i == n - 1) {
switch (preSign) {
case '+':
stack.push(num);
break;
case '-':
stack.push(-num);
break;
case '*':
stack.push(stack.pop() * num);
break;
default:
stack.push(stack.pop() / num);
}
preSign = s.charAt(i);
num = 0;
}
}
int ans = 0;
while (!stack.isEmpty()) {
ans += stack.pop();
}
return ans;
}
}
回到首页
刷 leetcode 500+ 题的一些感受
下一篇
《算法系列》之队列与堆