双因素方差分析(R)
目录
原理
双因素等重复试验的方差分析
假设前提和模型设定
离差平方和分解
检验统计量和拒绝域
例题
应用
双因素无重复试验的方差分析
假设前提和模型设定
离差平方和分解
检验统计量和拒绝域
例题
应用
原理
在单因素方差分析的基础上,双因素方差分析有两种类型,一种是无交互作用(双因素无重复试验)的双因素方差分析,一种是有交互作用(双因素等重复试验)的双因素方差分析。
双因素等重复试验的方差分析
假设前提和模型设定
设有交互作用的两个因素A,B作用于试验的指标,因素A有r个水平![]() ,因素B有s个水平
,因素B有s个水平![]() ,现对因素A,B的水平的每对组合
,现对因素A,B的水平的每对组合![]() 都作
都作![]() 次试验(成为等重复试验),得到结果:
次试验(成为等重复试验),得到结果:
| 因素 | ... | |||
| ... | ||||
| ... | ||||
| ... | ... | ... | ... | |
| ... |
由表可知,一共有r*s个总体,基于假设前提:
1.每个总体均服从正态分布,且方差相等,即,![]()
2.每个总体中抽取的样本相互独立
引入记号:
![]()
![]()
![]()
![]()
![]()
其中,![]() 为
为![]() 的效应,
的效应,![]() 为
为![]() 的效应,且
的效应,且
![]()
![]()
把![]() 表示为
表示为
其中,![]() 称为
称为![]() 因素水平和
因素水平和![]() 因素水平的交互效应,且
因素水平的交互效应,且
![]()
![]()
因此可把![]() 写成
写成![]() ,其中
,其中![]() ,各
,各![]() 独立
独立
对于这一模型,要检验以下三个假设:
离差平方和分解
引入记号:
![]()
![]()
![]()
![]()
总离差平方和:
其中,
组内离差平方和为
![]()
因素A的效应平方和为
![]()
因素B的效应平方和为
![]()
因素A、B交互效应平方和为
![]()
在实际计算中,可以使用以下公式简便计算:
记
![]()
![]()
![]()
![]()
计算
![]()
![]()
![]()
![]()
![]()
检验统计量和拒绝域
上述离差平方和的统计特性为
| 离差平方和 | 自由度 | 均值估计量 |
| SST | rst-1 | |
| SSW | rs(t-1) | |
| SSA | r-1 | |
| SSB | s-1 | |
| SSAB | (r-1)(s-1) |
当![]() 为真时,
为真时,
![]()
![]()
故拒绝域为
类似地,假设![]() 的拒绝域为
的拒绝域为
假设![]() 的拒绝域为
的拒绝域为
| 方差来源 | 离差平方和 | 自由度 | 均方 | F比 |
| 因素A | SSA | r-1 | ||
| 因素B | SSB | s-1 | ||
| 交互作用 | SSAB | (r-1)(s-1) | ||
| 误差 | SSW | rs(t-1) | ||
| 总和 | SST | rst-1 |
例题
一火箭使用四种燃料A,三种推进器B作射程试验,每种燃料与每种推进器的组合各发射火箭两次,得到射程结果服从双因素方差分析假设条件(以海里计),检验两个因素及交互效应是否显著
B1=c(58.2,52.6,49.1,42.8,60.1,58.3,75.8,71.5)
B2=c(56.2,41.2,54.1,50.5,70.9,73.2,58.2,51.0)
B3=c(65.3,60.8,51.6,48.4,39.2,40.7,48.7,41.4)
d=cbind(B1,B2,B3)
data=data.frame(d)
rownames(data)=c("A1","A1*","A2","A2*",
"A3","A3*","A4","A4*")
r=4
s=3
t=2
n=24
Xbar=mean(c(mean(data$B1),mean(data$B2),mean(data$B3)))
SST=sum((c(data$B1,data$B2,data$B3)-Xbar)**2)
tdata=data.frame(t(data))
SSA=s*t*((mean(c(tdata$A1,tdata$A1.))-Xbar)**2+
(mean(c(tdata$A2,tdata$A2.))-Xbar)**2+
(mean(c(tdata$A3,tdata$A3.))-Xbar)**2+
(mean(c(tdata$A4,tdata$A4.))-Xbar)**2)
SSB=r*t*((mean(data$B1)-Xbar)**2+
(mean(data$B2)-Xbar)**2+
(mean(data$B3)-Xbar)**2)
SSAB=0
m=function(rc,sc){
#引入目标数组函数简化代码,前述计算也可以用这个函数
y=c()
for(i in rc){
for(j in sc){
y=c(y,data[t*i-1,j],data[t*i,j])
}
}
return(y)
}
for(i in 1:r){
for(j in 1:s){
Xijbar=mean(m(i,j))
Xibar=mean(m(i,c(1,2,3)))
Xjbar=mean(m(c(1,2,3,4),j))
Xbar=mean(m(c(1,2,3,4),c(1,2,3)))
SSAB=SSAB+(Xijbar-Xibar-Xjbar+Xbar)**2
}
}
SSAB=t*SSAB
SSW=SST-SSA-SSB-SSAB
tab1=data.frame(matrix(nrow = 5,ncol = 5))
colnames(tab1)=c("方差来源","偏差平方和","自由度",
"均方","F比")
tab1[1,1]="因素A"
tab1[2,1]="因素B"
tab1[3,1]="交互作用"
tab1[4,1]="误差"
tab1[5,1]="总和"
tab1[1,2]=SSA
tab1[2,2]=SSB
tab1[3,2]=SSAB
tab1[4,2]=SSW
tab1[5,2]=SST
tab1[1,3]=r-1
tab1[2,3]=s-1
tab1[3,3]=(r-1)*(s-1)
tab1[4,3]=r*s*(t-1)
tab1[5,3]=r*s*t-1
tab1[1,4]=SSA/(r-1)
tab1[2,4]=SSB/(s-1)
tab1[3,4]=SSAB/((r-1)*(s-1))
tab1[4,4]=SSW/(r*s*(t-1))
tab1[1,5]=tab1[1,4]/tab1[4,4]
tab1[2,5]=tab1[2,4]/tab1[4,4]
tab1[3,5]=tab1[3,4]/tab1[4,4]
qf(1-0.05,r-1,r*s*(t-1))
qf(1-0.05,s-1,r*s*(t-1))
qf(1-0.05,(r-1)*(s-1),r*s*(t-1))由于
![]()
![]()
![]()
所以因素A,B及其交互效应都显著。
应用
A=c("A1","A1","A2","A2","A3","A3","A4","A4")
mdat=data.frame(A,B1,B2,B3)
library(reshape2)
mdata=melt(mdat,
id.vars = "A",
measure.vars = c("B1","B2","B3"),
variable.name = "B",
value.name = "range")
aov=aov(range~A+B+A*B,data=mdata)
summary(aov)双因素无重复试验的方差分析
假设前提和模型设定
如果在实际问题中,已经知道因素A、B不存在交互作用,就可以对每一个组合![]() 只做一次试验,得到实验结果
只做一次试验,得到实验结果
| 因素 | ... | |||
| ... | ||||
| ... | ||||
| ... | ... | ... | ... | ... |
| ... |
由表可知,一共有r*s个样本数据,基于假设前提:
1.每个样本数据均服从正态分布,且方差相等,即,
![]()
2.每个样本数据![]() 相互独立
相互独立
沿用上一试验的记号,由于不存在交互作用,![]() ,于是
,于是
![]()
则![]() ,其中
,其中![]() 且各
且各![]() 独立
独立
所需检验的假设为:
离差平方和分解
总离差平方和为
因素A的效应平方和为
![]()
因素B的效应平方和为
![]()
组内离差平方和为
![]()
为简便计算,可先计算其他离差平方和,再计算SSW
检验统计量和拒绝域
上述离差平方和的统计特性为
| 离差平方和 | 自由度 | 均值估计量 |
| SST | rs-1 | |
| SSA | r-1 |
|
| SSB | s-1 | |
| SSW | (r-1)(s-1) |
|
假设![]() 的拒绝域为
的拒绝域为
假设![]() 的拒绝域为
的拒绝域为
![]()
| 方差来源 | 离差平方和 | 自由度 | 均方 | F比 |
| 因素A | SSA | r-1 | ||
| 因素B | SSB | s-1 | ||
| 误差 | SSW | (r-1)(s-1) |
|
|
| 总和 | SST | rs-1 |
例题
有5个不同时间![]() 、4个不同地点
、4个不同地点![]() 空气中的颗粒物的含量(以
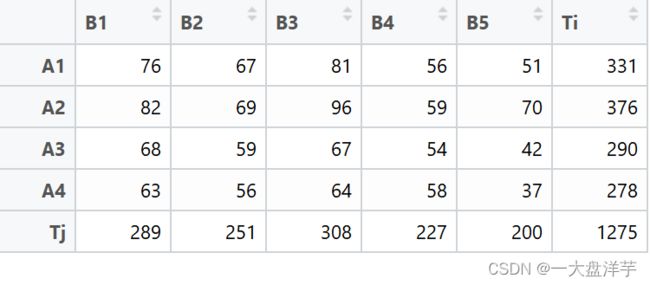
空气中的颗粒物的含量(以![]() 计)的数据,符合假设前提,检验是否显著
计)的数据,符合假设前提,检验是否显著
B1=c(76,82,68,63)
B2=c(67,69,59,56)
B3=c(81,96,67,64)
B4=c(56,59,54,58)
B5=c(51,70,42,37)
data2=data.frame(B1,B2,B3,B4,B5)
rowname=c("A1","A2","A3","A4")
rownames(data2)=rowname
r=dim(data2)[1]
s=dim(data2)[2]
n=r*s
m=function(rc,sc){
y=c()
for(i in rc){
for(j in sc){
y=c(y,data2[i,j])
}
}
return(y)
}
data2[5,1]=sum(m(1:r,1))
data2[5,2]=sum(m(1:r,2))
data2[5,3]=sum(m(1:r,3))
data2[5,4]=sum(m(1:r,4))
data2[5,5]=sum(m(1:r,5))
rownames(data2)=c(rowname,"Tj")
Ti=c()
for(i in 1:(r+1)){
Ti=c(Ti,sum(m(i,1:s)))
}
data2$Ti=Ti
SST=sum(m(1:r,1:s)**2)-(sum(m(1:r,1:s))**2)/r/s
SSA=sum(m(1:r,6)**2)/s-(sum(m(1:r,1:s))**2)/r/s
SSB=sum(m(5,1:s)**2)/r-(sum(m(1:r,1:s))**2)/r/s
SSW=SST-SSA-SSB
tab2=data.frame(matrix(nrow = 4,ncol = 5))
colnames(tab2)=c("方差来源","平方和","自由度","均方","F比")
tab2[1,1]="因素A"
tab2[2,1]="因素B"
tab2[3,1]="误差"
tab2[4,1]="总和"
tab2[1,2]=SSA
tab2[2,2]=SSB
tab2[3,2]=SSW
tab2[4,2]=SST
tab2[1,3]=r-1
tab2[2,3]=s-1
tab2[3,3]=(r-1)*(s-1)
tab2[4,3]=r*s-1
tab2[1,4]=tab2[1,2]/tab2[1,3]
tab2[2,4]=tab2[2,2]/tab2[2,3]
tab2[3,4]=tab2[3,2]/tab2[3,3]
tab2[1,5]=tab2[1,4]/tab2[3,4]
tab2[2,5]=tab2[2,4]/tab2[3,4]
qf(1-0.05,r-1,(r-1)*(s-1))
qf(1-0.05,s-1,(r-1)*(s-1))![]()
由于
![]()
![]()
所以因素A、B都显著。
应用
library(reshape2)
month=c("A1","A2","A3","A4")
Dat2=data.frame(month,B1,B2,B3,B4,B5)
rdata2=melt(Dat2,
id.vars = "month",
measure.vars = c("B1","B2","B3","B4","B5"),
variable.name = "province",
value.name = "concentration")
aov=aov(concentration~month+province,
data=rdata2)
summary(aov)