均值方差分析与风险资产组合
文章目录
- 引言
- 对均值和方差的解释
- 资产组合的均值方差特性
- 小结
引言
在前面的文章中,初步介绍了债券和股票的价值评估方法,从中可以看见,用什么样的贴现率来估计未来现金流的现值,是资产定价的关键。
在引入不确定性后,贴现率的确定变得更加困难。解决这个问题的方法是通过均值-方差分析的方法。而通过均值-方差分析衍生出的资本资产定价模型(CAPM)给出了确定资产贴现率的系统方法,同时也给出了资产定价的一个严谨理论框架。
在应用时,为了分析方便,将不同资产的均值方差描绘在以波动标准差为横轴,回报率为纵轴的坐标平面上。下面两幅图给出了我国股票和债券类资产的均值方差特性:

很明显,债券有着比股票低很多的回报率均值,但同时也有比股票小的多的波动。
对均值和方差的解释
均值是一种资产过去历史回报率的平均数,而方差是历史回报率的波动大小。
我们相信,均值和方差分别刻画了资产的收益和风险状况,是我们构建投资组合的输入条件。
事前和事后回报率
之前,我们很简单的介绍过资产回报率的概念。
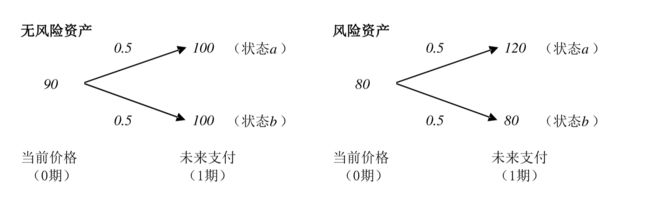
我们可以看出,两种资产在1期的期望支付均为100。
基于上面的设定,可以计算两种资产带给投资者的回报率。回报率分为事前回报率(ex ante rate of return) 和事后回报率(ex post rate of return) 。事前回报率是站在0期来计算的,事后回报率是站在1期来计算的。
事前回报率和事后回报率的最大差异在于不确定性是否揭示。 计算事前回报率时,资产回报尚未实现,回报率究竟会是多少还无法确知,只能预期。所以事前回报率是预期回报率。而事后回报率是发生回报后计算的。
对于上面的风险资产而言,0期计算事前回报率是:
E ( r ) = 0.5 × 120 + 0.5 × 80 80 − 1 = 25 % E(r)=\frac{0.5\times 120+0.5\times 80}{80}-1=25\% E(r)=800.5×120+0.5×80−1=25%
站在1期计算风险资产事后回报率有两种结果:
r a = 120 80 − 1 = 50 % r_a=\frac{120}{80}-1=50\% ra=80120−1=50%
r b = 80 80 − 1 = 0 % r_b=\frac{80}{80}-1=0\% rb=8080−1=0%
而对于无风险资产,可以知道事前事后回报率相同,都为11%。
现在我们引入风险溢价的概念,风险溢价(risk premium)是风险资产的期望回报率超出无风险资产期望回报率的部分,是对风险持有者承担风险的补偿。
所以上面例子中的风险溢价为: 25 % − 11 % = 14 % 25\%-11\%=14\% 25%−11%=14%
在资产定价中,我们都是站在现在,试图用资产的期望回报定出资产现在的价格。在期望回报给定后,只要再找出期望回报率,就能得到资产现在的价格。
这里的期望回报率,就是我们一开始所讲的贴现率。由于无风险回报率在现在就确定可知,所以风险资产定价的关键是找出其风险溢价。有了风险溢价,就有了资产回报率,也就有了资产价格。
在现实中,我们往往用一类资产过去实现的事后回报率来预测其期望回报率。类比例子中的风险资产,我们可以把这个风险资产想象称为某一类短期债券,观察这种债券的事后回报率表现,差不多事后回报率50%和0%出现的情况是55开,所以可以算出这种资产事后回报率均值是25%。这样,在预期这个资产的未来回报率的事后,往往会认为预期回报率等于过去事后回报率的均值。
方差与风险
收益率的方差来表征风险,而收益率的方差能用历史数据计算。
风险的本质在于不确定的未来。
协方差与相关系数
如果有两种资产,回报率分别为x和y,这两种资产的回报率协方差为:
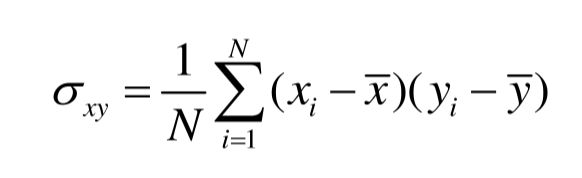
可以把协方差标准化为相关系数,相关系数的值域为[-1,+1],如果相关系数结果为-1,那么两个资产完全负相关,如果相关系数结果为+1,那么两个资产完全正相关。
其公式为:

资产组合的均值方差特性
进入正题,均值方差的核心内容——资产组合(protfolio)。
组合的收益风险特性当然会收到组合中各个资产的收益风险特性的影响,但是有趣的是,哪怕是同样的几种资产,只要组成组合的方式不一样,产生的资产组合的特性也会不同,所以才会有最优组合的概念。
一种无风险资产和一种风险资产的组合
从这种最简单的组合讨论起。
假设无风险资产和风险资产的回报率分别为 r j r_j rj和 r s r_s rs。其中,风险资产回报率的均值与标准差用 r ˉ s \bar{r}_s rˉs和 δ s \delta _s δs表示。
由于无风险资产收益率为常数,所以它与任何风险资产的回报率协方差都是0,他们也就不相关。假设投资在无风险资产和风险资产上的资产份额分别是 1 − w 1-w 1−w和 w w w,那么其组合的均值和方差分别是:

上面两个式子合并,替换掉 w w w,可得:
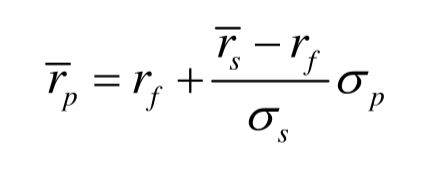
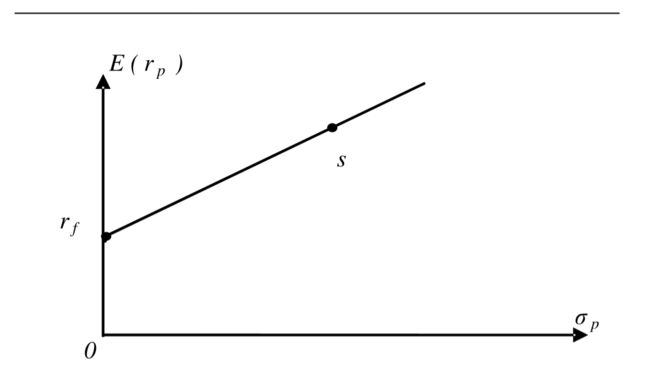
所以,组合资产回报率曲线如下图所示:
两种风险资产的组合
两种资产均值、方差和协方差如下:

投资在两种资产上的份额百分比分别为 w w w和 1 − w 1-w 1−w,则组合的预期回报为:

组合的回报率方差为:

根据上面的回报率方差,我们求权重 w w w在什么时候取得回报率方差的最小值,也就是:

将此权重 w w w带入均值表达式:
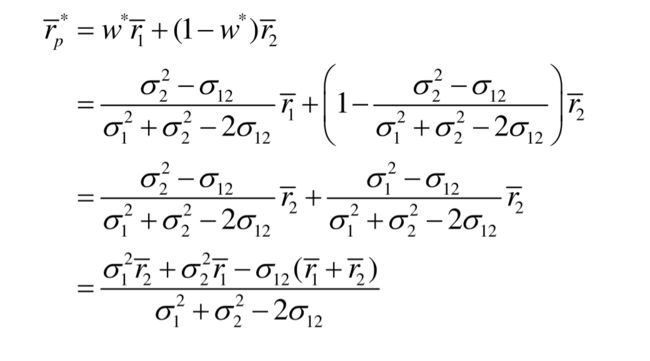
其实也就是求得如下图像的最小方差组合的点:

弯曲程度代表资产的相关性:

两种风险资产组合时,两种风险资产之间的相关性具有重要意义。图中表明,当两种资产完全负相关的时候,可以通过适当选择组合权重完全消除组合收益率的波动性。两种资产完全正相关的时候,无论如何也是消除不了收益率的波动性的。
不过两种资产完全正相关或者负相关在现实中一般不会发生。
多中风险资产组合的有效前沿
当超过两种风险资产时,讨论就要更复杂些,这些投资组合的收益风险状况不再在一根曲线上,而变成了一片区域。

在此,不做证明,直接说结论:
在均值-方差坐标系上,多种风险资产形成的组合区域边界是开口向右的、上下对称的双曲线。这条双曲线的上半边称为投资组合的“有效前沿(efficient frontier)”。由于在同等波动率上,处在有效前沿上的组合有最高的期望收益率,所以理性的投资者应该选择有效前沿上的组合。至于选择有效前沿上的哪个点,取决于投资者对于风险和收益率的权衡。
小结
作为普通人,最核心的就是要理解上述说明的核心思想,通过一系列的分散资产,可以通过相关性来减小资产投资的风险,说明风险对冲在一定程度上是可行的。