SG-Former：具有进化Token重新分配的自引导Transformer

摘要

https://arxiv.org/pdf/2308.12216.pdf
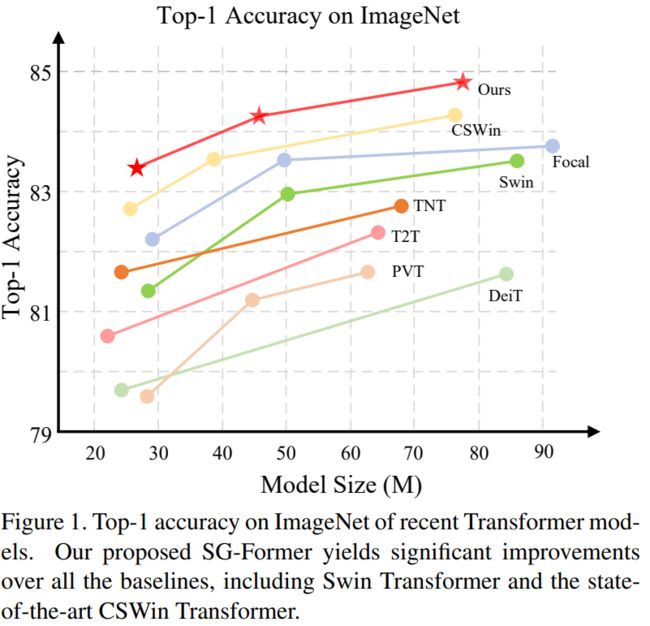
Vision Transformer在各种视觉任务中展示了令人印象深刻的成功。然而，其沉重的计算成本相对于Token序列长度呈二次增长，在很大程度上限制了其处理大型特征映射的能力。为了降低计算成本，以往的研究要么依赖于局限于局部小区域的细粒度自注意力，要么依赖于缩短序列长度导致粗粒度的全局自注意力。在本文中，我们提出了一种新的模型，称为自导向Transformer(SG-Former)，用于自适应细粒度的有效全局自注意力。我们方法的核心是利用显著性图，通过混合尺度的自主意力来估计，并在训练过程中自进化，根据每个区域的显著性来重新分配token。直观地说，我们将更多的Token分配给显著区域以获得细粒度的注意力，而将更少的token分配给次要区域以换取效率和全局感受野。所提出的SG-Former实现了优于SOTA的性能:我们的基本尺寸模型在ImageNet-1K上实现了84.7%的Top-1精度，在CoCo上实现了51.2mAP bbAP，在ADE20K上实现了52.7mIoU，比Swin Transformer高出+1.3% / +2.7 mAP/ +3 mIoU，计算成本更低，参数更少。代码可在https://github.com/OliverRensu/SG-Former上获得。

1、简介

Transformer模型[49]起源于自然语言处理（NLP），最近在视觉学习中展示了最先进的性能。视觉Transformer（ViT）的开创性工作[10]引入了自注意力模块，并明确地建模了图像补丁之间的长程依赖性，从而克服了卷积中本地感受野的固有限制，提高了各种任务的表现[9,27,56,70,74,1]。

尽管取得了巨大的成功，但自注意力的计算成本随着序列长度的增加而呈二次增长，这反过来又极大地限制了其在大规模输入上的应用。为了降低计算成本，ViT采用大步长补丁嵌入来减少序列长度。然而，这样的操作不可避免地导致自注意力只能应用于小尺寸特征图，而这些特征图的粒度很粗糙。为了在高清特征上计算自注意力，提出了一些方法[27, 9, 48]，将自注意力的区域限制在局部窗口而不是整个特征图上（即精细粒度的局部自注意力）。例如，Swin Transformer设计了窗口注意力，CSWin设计了跨形状注意力。因此，这些方法[27, 9, 48]牺牲了每个自注意力层中建模全局信息的能力。另一种方法[53, 59, 52]旨在将token聚合在整个键值对特征图上以减少全局序列长度（即粗糙粒度的全局注意力）。例如，Pyramid Vision Transfomer (PVT) [53]使用大步长的大核将token均匀地聚合在整个特征图上，从而得到整个特征图上统一的粗信息。

在这篇论文中，我们引入了一种新型的Transformer模型，称为自引导Transformer (SG-Former)，通过演化的自注意力设计实现了具有自适应精细粒度的全局注意力。SG-Former的核心思想在于，我们在整个特征图上保留了长程依赖性，同时根据图像区域的重要性重新分配Tokens。直观地说，我们倾向于将更多的Tokens分配给显著区域，这样每个Token可以在精细粒度上与显著区域进行交互，同时为了效率在次要区域分配更少的tokens。SG-Former根据重要性地图自适应地估计自注意力，保持全局感受野并关注显著区域的信息，实现高效处理。如图2所示，与PVT采用预先定义的策略将tokens均匀聚合不同，SG-Former根据从自身获得的重要性地图将更多的tokens重新分配给显著区域（例如狗），而将更少的tokens分配给次要区域（例如墙）。

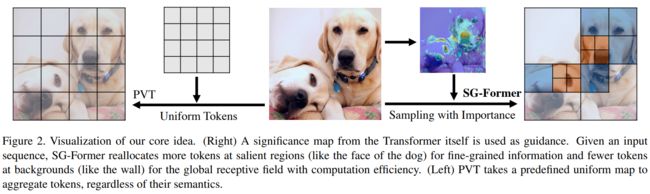
具体来说，我们保留查询Token，但重新分配键和值Token，以实现高效的全局自注意力。图像区域的重要性以得分图的形式通过混合尺度自注意力估计，并进一步用于指导token重新分配。换句话说，给定一个输入图像，Token重新分配是通过自引导完成的，这表明每个图像都经历了独特的、仅为自己定制的Token重新分配。因此，重新分配的Tokens受到人类先验的影响较小。此外，这种自引导随着训练过程中精确性地图预测的逐步提高而不断发展。重要性地图极大地影响了重新分配的效率，因此我们提出了一种混合尺度的自注意力，它在同一成本下实现了与Swin相同的性能。混合尺度自注意力的各种粒度信息是通过将头部分组和多样化每个组以不同的注意力粒度来实现的。混合尺度自注意力还为整个Transformer提供了混合尺度信息。

我们的贡献因此总结如下：

• 我们引入了一种新型的Transformer模型，称为SG-Former，通过统一混合尺度信息提取，在单个自注意力层内包括精细的局部和全局粗糙的信息。借助统一的局部全局混合尺度信息，我们预测了重要性地图以识别区域重要性。
• 使用重要性地图，我们模拟了自引导注意力以自动定位显著区域，并保持显著区域的精细粒度以准确提取信息，而将次要区域保持粗糙粒度以降低计算成本。
• 我们评估了所提出的Transformer主干在各种下游任务上的性能，包括分类、目标检测和分割。实验结果表明，SG-Former在模型大小相似的情况下始终优于之前的Vision Transformers。

2、相关研究

视觉Transformer。视觉Transformer（ViT）[11]源自用于自然语言处理的Transformer[49]，首次将纯Transformer架构引入计算机视觉。这种架构在图像分类方面相对于以前的卷积网络取得了令人瞩目的改进。像JFT-300M这样的大规模数据集对ViT的训练要求限制了其在各种任务中的应用。有些工作[45、46、36、39、38]提出了复杂的数据增强、正则化、知识蒸馏和训练策略。最近，一些工作为检测[55、43]、分割[42、71、37]、恢复[35]、检索[12]、重识别[19]设计了基于ViT的更好的Transformer架构，并提高了扩展性[41、4]和鲁棒性[22]。与这些工作不同，最近的工作[9、27、59、68、66、47、65、23]旨在设计用于一般视觉任务的通用Transformer主干，而不是针对某些特定任务。这些Transformer与原始ViT的最显著区别在于，它们采用分层架构，遵循与卷积相同的思路，而不是ViT中的单尺度特征，并且在处理大尺寸特征图时使用更有效的自注意力。值得注意的是，已经证明整体架构[63、64]，而不是专门的注意力操作，在实现卓越性能方面发挥着至关重要的作用。因此，这一洞察导致了更强大和更有效的架构[3、29]。

高效深度学习。设计具有最小训练时间[61、32、62]、低推断成本[20、67、60、13、30、14]和减少数据需求[51、25、26]的高效深度学习模型一直是一个长期的追求。就ViT而言，当处理大量Tokens（例如NLP中的长文档或计算机视觉中的高分辨率图像）时，高效的自注意变得至关重要，因为自注意可以导致计算和内存成本的二次方。一方面，局部精细粒度的自注意限制了查询Token在预定义窗口内的邻近Token上的注意力。Swin Transformer [27]将特征图拆分为窗口形状的区域以限制局部自注意力。Axial attention [21]提出计算条带窗口注意力。Focal [59] Transformer预先定义了粗糙粒度区域，并使用不同的粒度对不同的区域进行自注意力计算。CSWin [9]设计了带有水平和垂直条带的窗口。CSWin将头部拆分为并行组，并对不同的组应用不同的注意力。另一方面，全局粗糙粒度的自注意保持了在自注意力中建模全局依赖性的能力，但面临着粗糙粒度的信息处理。PVT [53]试图通过令牌减少来保持全局接收场，但导致粗糙粒度的自注意。Focal Transformer [59]预先定义了对周围环境的更多关注和对远离位置的较少关注。然而，这种归纳偏差限制了模型对远离当前令牌位置的显著对象的关注能力。与以前的工作不同，我们提出给自注意模块更多的灵活性，让它只通过一些预定义的指导而不是特定的方法来找到降低计算成本的最佳方法。

3、方法

3.1、概述

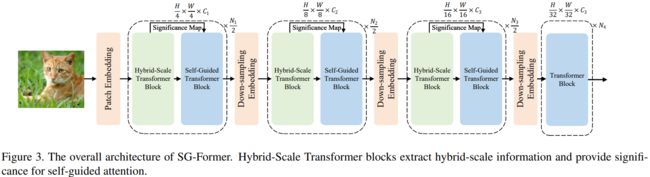
SG-Former的整体流程如图3所示。SG-Former与之前的CNN和Transformer模型共享相同的patch嵌入层和四阶段金字塔架构[17,53,27,9]。输入的图像$X\in R^{H\times W\times 3}$经过patch嵌入层以4×的速度下采样。在两个阶段之间存在一个以2×速率为下采样的层。因此，在第i阶段特征图的大小为$\frac{H}{2^{i+1}}\times \frac{W}{2^{i+1}}$。除了最后一个阶段外，每个阶段都包含N个Transformer块，这些块由两种类型的块反复组成：(i)一个混合尺度Transformer块；(ii)一个自引导Transformer块。混合尺度自注意力提取混合尺度对象和多粒度信息，引导区域重要性；其细节将在第3.3节中介绍。自引导自注意力根据混合尺度Transformer块的重要性信息建模全局信息，同时在显著区域保持更精细粒度；其细节将在第3.2节中介绍。

3.2、自引导注意力

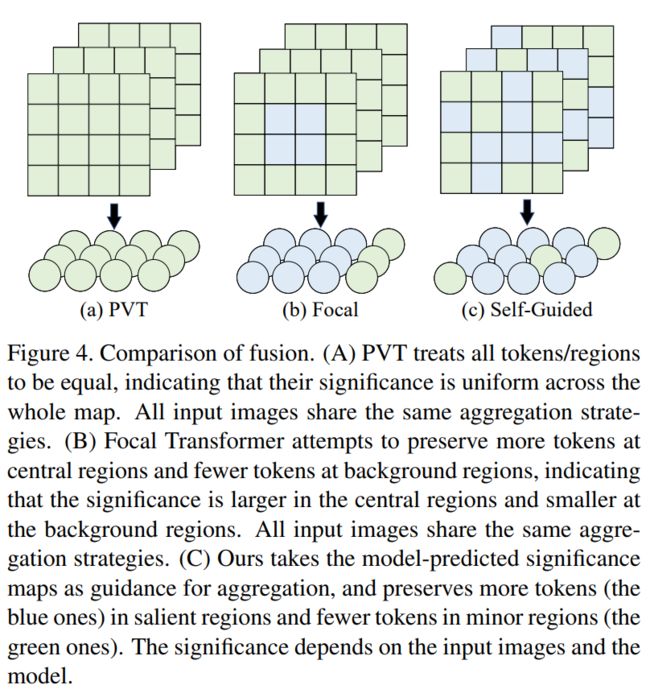
尽管普通的自注意力具有建模远距离信息的能力，但其计算成本和内存消耗与序列长度呈二次关系，这限制了其在各种计算机视觉任务中的大尺寸特征图中的应用，例如分割和检测。最近的工作[53,52]建议通过合并少量Tokens来降低序列长度和Token聚合。然而，这种聚合方式对待每个Token都是平等的，忽略了不同Token之间的固有意义差异。这种聚合面临两个问题：(i)在显著区域，信息可能会丢失或与不相关信息混淆；(ii)在次要区域或背景区域，对于简单的语义来说，很多Tokens（占比较高）是冗余的，同时需要大量计算。受此观察的启发，我们提出使用自引导注意力，即以重要性为指导来聚合Tokens。具体来说，在显著区域，为获取更精细的信息而保留更多的Tokens；而在次要区域，仅保留较少的Tokens以保持全局自注意力并同时降低计算成本。如图4所示，“自引导”指的是Transformer本身在训练期间决定了我们的计算成本降低策略，而非人类引入的先验知识，例如Swin中的窗口注意力[27]、CSWin中的交叉形状注意力[9]、PVT中的静态空间缩减[53]。

输入特征图$X\in {\mathbb{R}}^{h\times w\times c}$首先被投影到查询（Query, Q）、键（Key, K）和值（Value, V）。接下来，H个独立的自注意力头并行计算自注意力。为了在保持注意力后特征图大小不变的同时降低计算成本，我们固定Query的长度，但使用重要性引导的聚合模块（IAM）对K和V的tokens进行聚合。
$$\begin{array}{l}Q=X{W}^Q,\\ K=\mathrm{IAM}(X,S,r)W^K,\\ V=\mathrm{IAM}(X,S,r)W^V.\end{array}\text{\hspace{1em}(1)}$$

IAM的目标是在显著区域将更少的tokens聚合为一个（即保留更多信息），而在背景区域将更多的tokens聚合为一个（即保留更少信息）。在式(1)中，重要性地图$S\in {\mathbb{R}}^{h\times w}$包含多个粒度的区域重要性信息（见第3.3节）。我们按升序对重要性地图的值进行排序，并将S均匀地分为n个子区域$S^1，\dots ，S^n$。因此，$S^n$和$S^1$分别是最高重要性和次要区域。同时，根据$S^1，\dots ，S^n$将所有tokens分成$X^1，\dots ，X^n$组。在式(1)中，r表示每r个tokens被聚合成一个token的聚合率。我们在不同重要性的区域设置不同的聚合率$r^1，\dots ，r^n$，这样每个子区域都有一个聚合率，子区域越重要，聚合率越小。不同阶段的具体r值列于表1中。因此，IAM逐组聚合输入特征$X^1，\dots ，X^n$，每组用不同的聚合率重新分配tokens并将每组的tokens连接起来。
$$\begin{array}{l}{\hat{X}}^i=F\left(X^i,r_i\right),\\ \hat{X}=\mathrm{Cat}\left({\hat{X}}^1,\cdots ,{\hat{X}}^n\right)\end{array}\text{\hspace{1em}(2)}$$
其中$F(X,r)$是聚合函数，我们通过具有输入维度r和输出维度1的全连接层来实现它。${\hat{X}}_i$中的tokens数量等于$X^i$中的token数量除以$r_i$。

3.3、混合尺度注意力

混合尺度注意力服务于两个目的：(i)以不高于Swin Transformer中的窗口注意力的计算成本来提取混合尺度的全局和精细信息；(ii)为自引导注意力提供重要性。

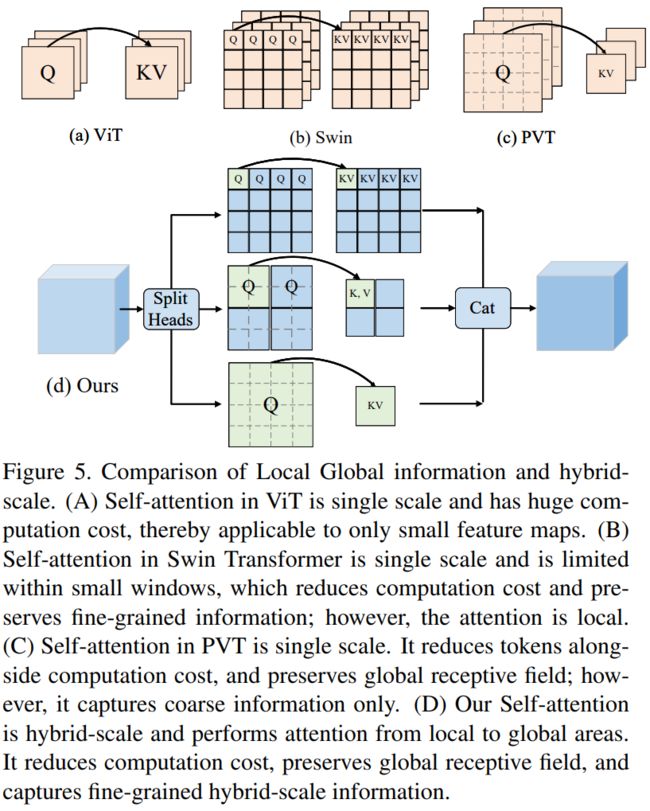
如图5所示，输入特征X被投影成查询（Query，Q）、键（Key，K）和值（Value，V）。然后，多头自注意力采用H个独立头。通常，这些H个独立头在相同的局部区域内执行，因此缺乏头多样性。相比之下，我们将H个头均匀地分成h组，并将混合尺度多感受野注意力注入到这h组中，每组有$\frac{H}{h}$个头。在属于第j组的第i个头中，使用尺度$s_j$（其中j=1，…，h），将｛K，V｝中的每个$s_j\times s_j$个Tokens合并为一个token。接下来，我们将｛Q，K，V｝分成窗口。｛K，V｝的窗口大小设置为M，并且在所有组中保持不变。为了使｛Q｝的窗口大小与｛K，V｝中的Token合并对齐，｛Q｝的窗口大小选择为$s_{j}M\times s_{j}M$，是｛K，V｝窗口大小的$s_j$倍。注意力的接收野被显著地扩大了$s_j$倍：
$$\begin{array}{l}{Q}_i=X{W}_i^Q,\\ K_i=\mathrm{Merge}\left(X,s_j\right)W_i^K,\\ V_i=\mathrm{Merge}\left(X,s_j\right)W_i^V,\end{array}\text{\hspace{1em}(3)}$$
其中，$\mathrm{Merge}\left(X,s_j\right)$表示将X中的每个$s_j\times s_j$个tokens合并为一个token，这可以通过步长为$s_j$的卷积来实现。一个特殊情况是当$s_j$等于1时，没有token合并，并且｛Q，K，V｝具有相同大小的窗口。
$$\begin{array}{c}{\text{ Atten }}_i={\mathrm{Softmax}}_{(}\left(\frac{P\left(Q_i,s_{j}M\right)P\left(K_i^{\top },M\right)}{\sqrt{d_h}}\right),\\ h_i={\mathrm{Atten}}_{i}P\left(V_i,M\right)\end{array}\text{\hspace{1em}(4)}$$

其中，$P\left(X,s_{j}M\right)$表示窗口大小为$s_{j}M\times s_{j}M$的窗口划分。$Atten{n}_j$是注意力图。有一个特殊情况：$s_{j}M\times s_{j}M$等于$h\times w$，此时不需要窗口划分，｛K，V｝中的所有tokens都被｛Q｝处理，从而提取全局信息。

将当前token的显著性设为所有token及其当前token的乘积之和：
$$\begin{array}{l}{S}_i=\frac{1}{hw}{\sum }_{m=1}^{hw}{\mathrm{Atten}}_i^{m,n},\\ S={\sum }_{i=1}^h{S}_i,\end{array}\text{\hspace{1em}(5)}$$

其中，S是通过将$S_i$求和得到最终显著性图，用于同时具有全局和精细信息的混合尺度指导。

3.4、Transformer块

通过两种自注意力机制，我们相应地设计了两种类型的Transformer块。这两种Transformer块仅在注意力层上有所不同，而在其他方面均保持一致：

$$\begin{array}{r}{\hat{X}}^i=\mathrm{MS}-\text{ Attention }\left(\mathrm{LN}\left(X^{i-1}\right)\right)+X^{i-1},\\ {\hat{X}}^i=\mathrm{MLP}\left(\mathrm{LN}\left(X^{i-1}\right)\right)+X^{i-1},\end{array}\text{\hspace{1em}(6)}$$

$$\begin{array}{r}{\hat{X}}^i=\mathrm{SG}\text{-Attention }\left(\mathrm{LN}\left(X^{i-1}\right)\right)+X^{i-1},\\ {\hat{X}}^i=\mathrm{MLP}\left(\mathrm{LN}\left(X^{i-1}\right)\right)+X^{i-1},\end{array}\text{\hspace{1em}(7)}$$

如图3所示，前三个阶段使用我们提出的混合尺度或自引导Transformer块进行定制，而对于最后一个阶段，我们使用标准的Transformer块，类似于之前的Transformer模型[45, 11, 27, 9]。需要注意的是，前三个阶段中Transformer块的数量（即N_1、N_2和N_3）是偶数，而最后一个阶段中Transformer块的数量（即N_4）可以是偶数或奇数。

3.5、Transformer架构变体

我们构建了三种尺寸的小型（SG-Former-S）、中型（SG-Former-M）和基础型（SG-Former-B）模型，以与其它Transformer进行公平比较。它们在不同方面的差异，包括通道数、注意力头数以及每个阶段的块数，详细地列在表1中。小型和中型模型在每个阶段都有两个尺度，而基础型模型在第一阶段有四个尺度，第二阶段有三个尺度。借鉴[9,40]，我们还采用了卷积补丁嵌入、局部增强细节特定前馈层，为简化起见，这些细节未在公式中展示。

4、实验

为了证明SGFormer骨干网的架构优势，我们在ImageNet1K分类[8]、COCO对象检测[24]和ADE20K语义分割[72]上进行了实验。此外，我们还分析了单尺度和混合尺度的自注意的影响，以及不同导向对自进化注意的影响。

4.1、ImageNet-1K的分类

为了公平地与之前的方法进行比较，我们遵循相同的训练设置[45,9]。具体而言，所有模型在ImageNet-1K上训练300 epoch，输入分辨率为224×224，批处理大小为1024。对于优化，我们采用权值衰减为0.05，余弦学习率衰减为线性热身20次的AdamW优化器，将峰值学习率设置为1e3。对于数据增强和正则化，我们与CSWin[9]保持一致，包括RandAugment、指数移动平均、数据混合、标签平滑、随机深度和随机擦除。在推理过程中，我们调整大小并将裁剪中心设置为224×224。

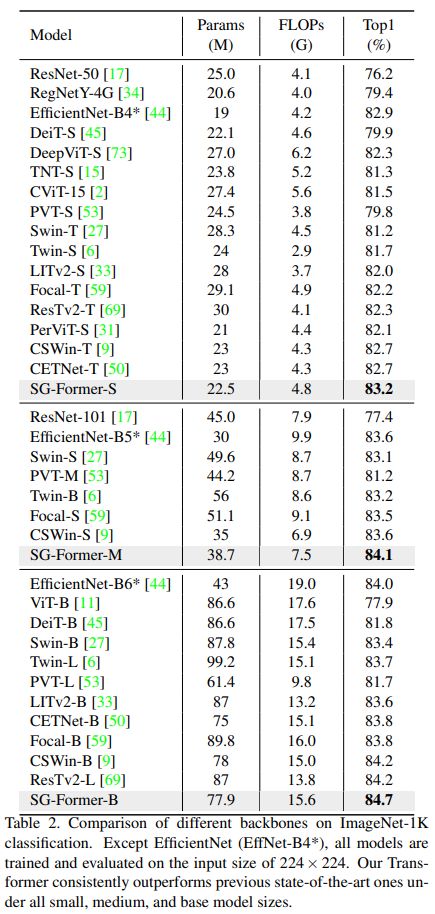
在表2中，我们将SG-Former与最先进的CNN和Transformer架构进行了比较。SG-Former在相似的参数和计算成本下始终优于竞争对手。具体来说，SG-Former在小型、中型和基础模型下分别实现了83.2%、84.1%和84.7%的Top-1准确率。将SG-Former主干网络与CNN主干网络进行比较，SG-Former主干网络是第一个超越之前最先进的基于CNN的主干网络EfficientNet的Transformer主干网络，而EfficientNet采用了神经网络架构搜索。尽管EfficientNet来自于神经网络架构搜索，但我们手动设计的SG-Former-S/M/B仍然实现了+0.3/+0.5/+0.6的Top-1准确率提升。

与基准Transformer DieT相比，我们的小型模型甚至通过+1.4显著优于基础模型，而参数和计算成本分别仅为基型的四分之一（86.6M→ 24.2M和17.6G→ 4.8G）。SG-Former S/M/B相对于Swin T/S/B实现了+2.0/+1.0/+1.2的性能提升。与最先进的Transformer CSWin相比，SG-Former S/M/B在相似的参数下实现了+0.5/+0.5/+0.4的性能提升。

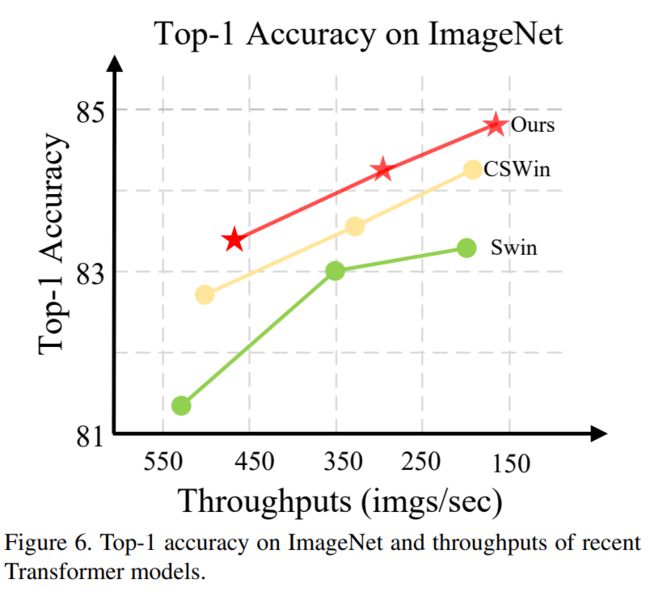
吞吐量和性能。通过实验和性能展示，如图6所示，我们在单个RTX 2080 Ti上评估了不同模型的吞吐量。SG-Former在相似的性能下是最快的，或者在相似的推断速度下具有最佳的性能。

具有更高输入分辨率的分类。按照[9,27]的相同设置，我们将模型的输入分辨率调整为384× 384。使用ImageNet-1K上的预训练模型，输入分辨率为224×224，我们对其进行了30次微调。我们采用AdamW作为优化器，权重衰减为1e-8。学习率设为5e-6，随机下降路径设为0.4。

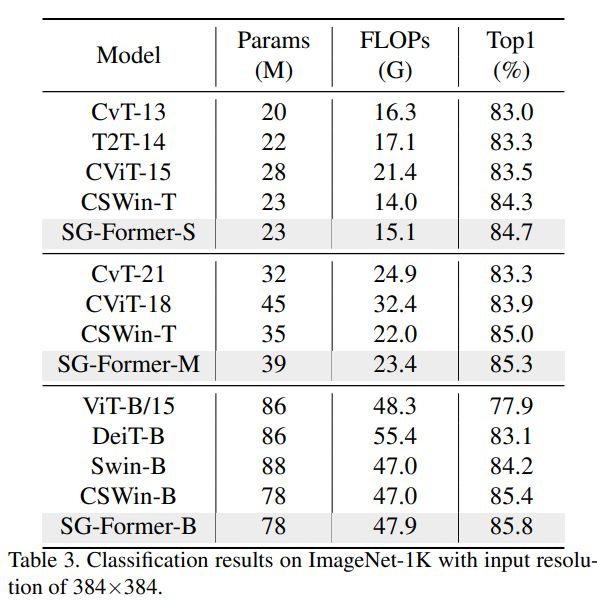
如表3所示，SG-Former在相似的参数下显著优于其对应模型。具体来说，我们的基础模型在性能上比Swin-B高出1.6。SGFormer-S/M/B分别比之前的最佳模型CSWin高出+0.4、+0.3、+0.4。

4.2、目标检测和实例分割

我们以ImageNet预训练作为初始化，Mask R-CNN[16]作为检测管道，评估SG-Former主干在目标检测和实例分割方面的性能。在COCO2017[24]上对所有模型进行训练和评估，其中118k图像用于训练，5K图像用于验证。我们遵循相同的设置[27,53,9]，使用1x时间表进行12个epoch的训练，使用3x时间表进行36个epoch的训练。对于1x调度，我们进行单尺度训练，短边输入图像800张，长边输入图像不超过1333张。对于3 ×时间表，我们通过随机调整其短边的大小来使用多尺度训练[480,800]。我们将SG-Former骨干网与CNN骨干网进行比较:ResNet[17]、ResNeXt(X)[57]和Transformer骨干网Swin[27]、PVT[53]、Focal[59]、CSWin[9]、Twin[6]。

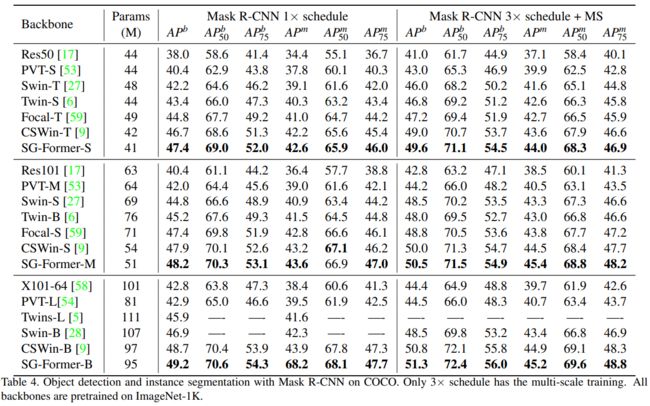
在表4中，我们报告了使用MaskRCNN[16]管道的结果，并分别将边界框mAP和掩码mAP作为对象检测和实例分割的评估指标。与CNN骨干网相比，我们的方法在ResNeXt上取得了令人难以置信的改进，在1x调度下提高了+6.4，在3x调度下提高了+6.9。与Transformer主干相比，SG-Former也显示出优势。SG-Former改进Swin Transformer(最知名的变压器)和CSWin Transformer(最先进的变压器)。这种优势来自于我们模型中保存更细粒度信息和全局接受域的能力。

4.3、ADE20K上的语义分割

我们使用ADE20K数据集进一步评估SG-Former骨干网在语义分割上的性能。我们以语义FPN、UperNet为基本框架。ADE20K是一个广泛使用的语义分割数据集，有150个语义类别，包含20K张用于训练的图像和2K张用于验证的图像。在相同的设置[9]下，我们以Semantic FPN和Upernet为框架，通过mmsegmentation实现[7]。对于SemanticFPN，我们采用权重衰减为0.0001的AdamW作为优化器，对于80K次迭代，学习率也为0.0001。我们将mIoU作为评估指标。对于UperNet，我们采用权值衰减为0.01的AdamW作为优化器，迭代次数为160K，批大小为16。在训练开始时进行1500次迭代预热，学习率为6 × 10e-5，学习率线性衰减。增强包括随机翻转、随机缩放和随机光度量失真。训练时输入大小为512 × 512。对于SemanticFPN，我们采用权重衰减为0.0001的AdamW作为优化器，对于80K次迭代，学习率也为0.0001。我们以mIoU作为评价指标，报告了语义FPN的单尺度测试结果，以及UperNet的单尺度和多尺度测试结果。

我们在表5中报告了结果，SG-Former在相似的参数下优于所有竞争对手。具体来说，当使用Semantic FPN时，SG-Former取得了50.6 mIoU，并以10%的模型大小优势超越了Swin Transformer 4.6 mIoU。当框架为UperNet时，我们的SG-Former取得了52.7 mIoU，以3 mIoU优势超越了Swin。

4.4、消融实验

单尺度和混合尺度自注意力。我们的混合尺度Transformer块具有两个功能：1）利用混合粒度信息捕获和识别不同大小的对象；2）为自引导注意力提供混合尺度重要性证明，以便在显著区域聚合背景tokens并保留更细粒度的信息。

我们在表6中对利用混合粒度信息捕获和识别不同大小物体的功能进行了消融实验。单尺度（局部）表示没有token聚合，只有窗口注意力并且只有一个尺度，而单尺度（全局）表示聚合率足够大，sM × sM = H × W，自注意力在全球范围内执行并且也只有一个尺度。我们的混合尺度自注意力分别比局部注意力和全局注意力高出1.0和0.6。

显著性指导。为了评估显著性地图的影响，在每个模块中，我们将第一个混合尺度Transformer块保持不变，但在第二个自引导Transformer块中更改重要分数图源。我们手动将整个显著性图上的所有位置的显著性图定义为相等作为比较。混合尺度自注意力层提供具有混合尺度信息的显著性图，但我们仅使用全局尺度或局部尺度的显著性。

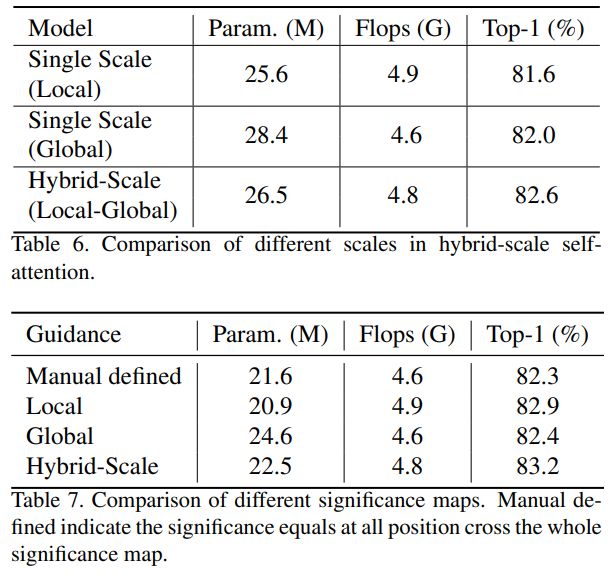
如表7所示，混合尺度的显著性优于手动定义的基线，该基线将所有区域的重要性等同对待，高出0.9。包含局部细粒度区域重要性信息的局部尺度显著性比包含全局粗粒度区域重要性信息的全局尺度显著性表现更好，而混合尺度显著性图在所有竞争对手中表现出色。

5、结论

在本文中，我们提出了一种名为自引导Transformer（SG-Former）的新型Transformer主干网络。关键动机是根据混合尺度指导聚合tokens，这明确考虑了跨越整个特征映射的长距离依赖关系，并关注更多的前景tokens以获取更精细粒度的信息，同时合并更多背景tokens以提高计算效率。在分类、检测和分割实验中，SG-Former取得了令人满意的结果:我们的基本尺寸模型在ImageNet-1K上达到了84.7%的Top-1精度，在CoCo上达到了51.2mAP bbAP，在ADE20K上达到了52.7mIoU，超过Swin Transformer +1.3% /+2.7 mAP/ +3 mIoU，且计算成本更低。