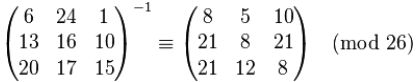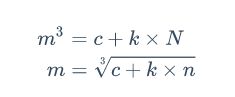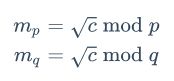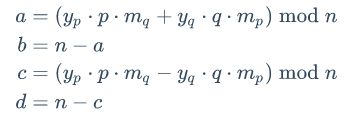密码学基础
文章目录
- **密码学基础**
-
- **一·古典密码**
-
- 1、栅栏密码(置换,代换)
-
-
- 变形
-
- 2、换位密码(代换密码)
-
- 2.1、单表替换密码
- **凯撒密码**
- **仿射密码**
- 2.2、多表替换密码
- **维吉尼亚密码**
- **希尔密码**
- **猪圈秘密**
- **培根密码**
- **二·现代密码**
-
- 1、对称密码
-
- 1.1、分组加密
-
- **DES**
- **AES**(CTF中,不知秘钥无法破解)
- **TEA**
- 1.2、流加密(序列密码)
- 2、**加密模式**(分组模式)
-
- ECB
- CBC
- 3、非对称密码
-
- **RSA**
-
- **攻击**
- RSA衍生算法--Rabin算法
密码学基础
一·古典密码
- 古典密码编码方法归根结底主要有两种,即置换和代换。
- 把明文中的字母重新排列,字母本身不变,但其位置改变了,这样编成的密码称为置换密码。最简单的置换密码是把明文中的字母顺序倒过来,然后截成固定长度的字母组作为密文。
- 代换密码则是将明文中的字符替代成其他字符。
1、栅栏密码(置换,代换)
N栏栅栏加密,把要加密的明文分成N个一组,然后把每组的第1个字符组合,每组第2个字符组合…每组的第N(最后一个分组可能不足N个)个字符组合,最后把他们全部连接起来就是密文,N就是栏数
明文:The quick brown fox jumps over the lazy dog
去空格:Thequickbrownfoxjumpsoverthelazydog
分组:Th eq ui ck br ow nf ox ju mp so ve rt he la zy do g
第一组:Teucbonojmsvrhlzdg
第二组:hqikrwfxupoeteayo
密文:Teucbonojmsvrhlzdghqikrwfxupoeteayo
变形
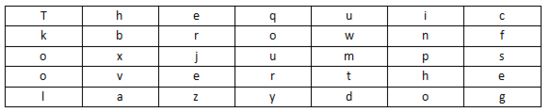
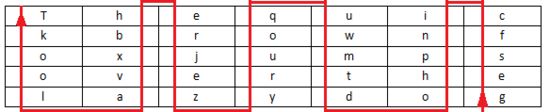
将明文去空格后按顺序放入5×7的表格中,即栏数为5,分为7组
换顺序读取
带秘钥栅栏
按字母在字典中出现的先后顺序排序
2、换位密码(代换密码)
2.1、单表替换密码
明密文一一对应,可以使用词频分析http://quipqiup.com/
凯撒密码
明文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后被替换成密文
明文:The quick brown fox jumps over the lazy dog
偏移量:1
密文:Uif rvjdl cspxo gpy kvnqt pwfs uif mbaz eph
偏移量为10:Avocat(A→K)
偏移量为13:ROT13
偏移量为-5:Cassis(K6)
偏移量为-6:Cassette(K7)
仿射密码
它的加密函数是E(x)=(ax+b)(mod m),其中
a和m互质;
m是字母的数目。
解密函数是D(x)=a−1(x−b)(mod m),其中a−1是a在Zm群的乘法逆元
以(5x+8)mod26为例:

因为密文明文必是一一对应的,所以可以用爆破的方法解密
2.2、多表替换密码
由多个简单的代替密码组合构成
维吉尼亚密码
使用一系列凯撒密码组成密码字母表的加密算法多表密码的一种最简单形式
例:
明文:come greatwall
密钥:crypto
密文:efkt zferrltzn
维吉尼亚密码破解:
破译维吉尼亚密码的关键在于它的密钥是循环重复的。如果我们知道了密钥的长度,那密文就可以被看作是交织在一起的凯撒密码,而其中每一个都可以单独破解
卡西斯基试验
在大批量明密文对样本中,如果两个相同字母序列间距正好是密钥长度的倍数时,也可能产生相同的密文序列.寻找重复出现的字母序列,并求其长度
工具:
https://www.mygeocachingprofile.com/codebreaker.vigenerecipher.aspx
https://www.guballa.de/vigenere-solver
明文:we are discovered save yourself
密钥:deceptive
密文:ZICVTWQNGRZGVTWAVZHCQYGLMGJ
解密:
1、在密文中标出重复的字符结构——VTW;
2、两个字符结构的起始位置分别为4和13;
3、两个起始点的距离是9;
4、9的因数有3和9;
5、根据步骤4出现的因数,确定密钥的可能长度是3位或9位
希尔密码
每个字母当作26进制数字:A=0,B=1,C=2等,一串字母当成n维向量,跟一个n×n的矩阵相乘,再将得出的结果模26。
密文即为:POH
解密
猪圈秘密
(英语:pigpen cipher),亦称共济会密码(英语:masonic cipher)或共济会员密码(英语:Freemason’scipher),是一种以格子为基础的简单替代式密码。即使使用符号,也不会影响密码分析,亦可用在其它替代式的方法。
变形
一一对应,单表映射
培根密码
培根密码实际上就是一种替换密码,根据所给表一一对应转换即可加密解密。它的特殊之处在于:可以通过不明显的特征来隐藏密码信息,比如大小写、正斜体等,只要两个不同的属性,密码即可隐藏。
二·现代密码
1、对称密码
在对称密码中,加密者不解密者所使用的秘钥相同
对称加密又分为分组加密和序列密码
1.1、分组加密
分组密码,也叫块加密(block cyphers),一次加密明文中的一个块。是将明文按一定的位长分组,明文组经过加密运算得到密文组,密文组经过解密运算(加密运算的逆运算),还原成明文组。
DES
密钥的长度64位,8个字节。(秘钥太短,易爆破)
DES全称为Data Encryption Standard,是典型的块加密,其基本信息如下:
- 使用64位秘钥中的56位,剩余的8位要么丢弃,要么作为奇偶校验位
- 输入64位
- 输出64位
- 明文经过16轮迭代得到密文

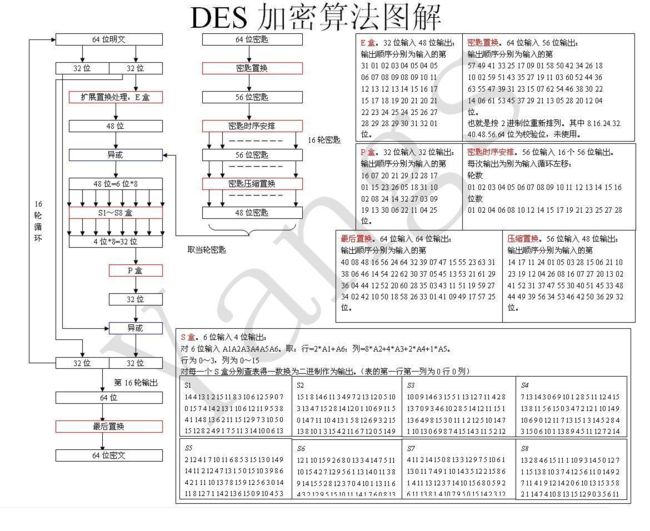
每轮加密:

s盒:
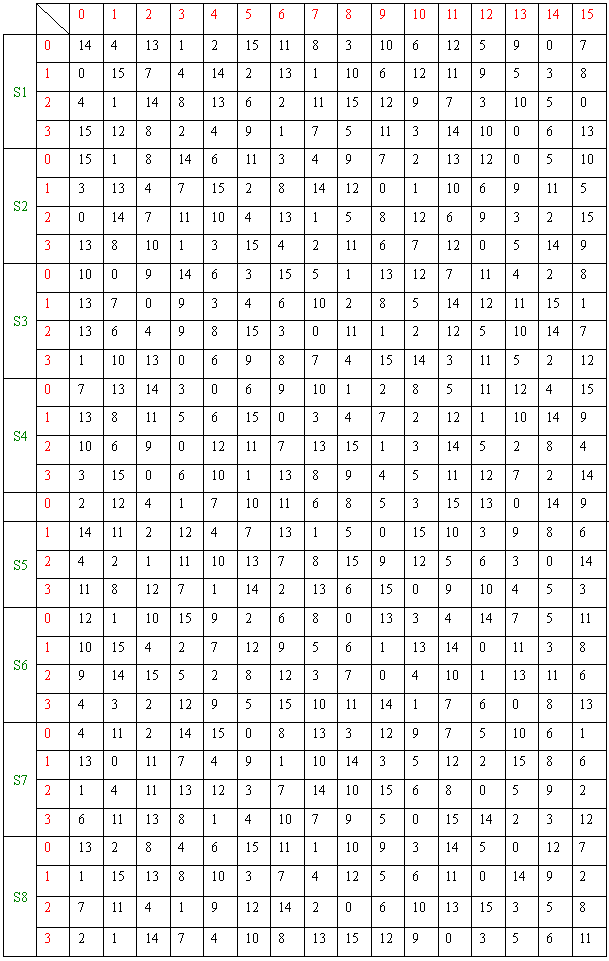
AES(CTF中,不知秘钥无法破解)
密钥的长度可以为128、192和256位,也就是16个字节、24个字节和32个字节
AES全称为Advanced Encryption Standard,典型的块加密,被设计来取代DES。其基本信息如下:
-
分组长度和秘钥长度均可变,可以有以下几种数值
128bit192bit
256bit
-
明文经过10、12、14轮迭代得到密文
TEA
1.2、流加密(序列密码)
序列密码,也叫流加密(stream cyphers),一次加密明文中的一个位。是指利用少量的密钥(制乱元素)通过某种复杂的运算(密码算法)产生大量的伪随机位流,用于对明文位流的加密。
RC4
每次加密明文中的一个字节
秘钥长度可变,1-256字节
基本流程:
- 初始化S和T
- 计算排列S, j从0到255
- 产生不明文等长秘钥流
- 加密
2、加密模式(分组模式)
- ECB
- CBC
- CFB
- OFB
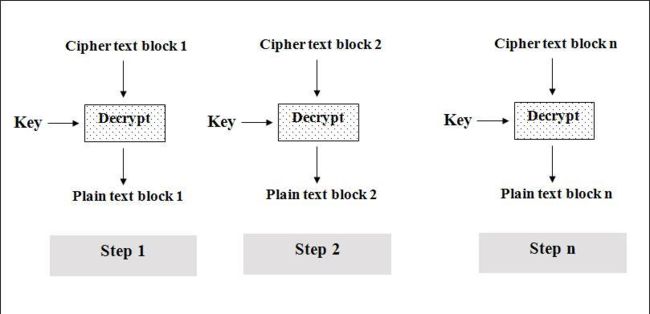
ECB
ECB(Electronic Code Book)/电码本模式

特点
1.简单,有利于并行计算,误差不会被传送;
2.不能隐藏明文的模式;在密文中出现明文消息的重复
3.可能对明文进行主动攻击;加密消息块相互独立成为被攻击的弱点
缺点
明密文一一对应,易破解
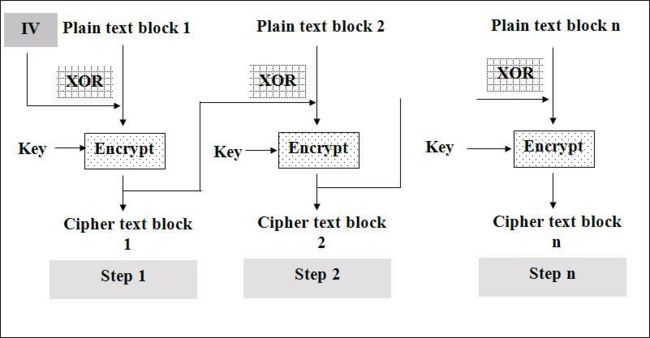
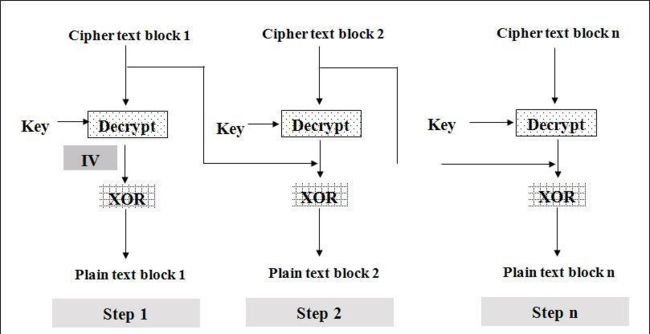
CBC
CBC(Cipher Block Chaining)/密码分组链接模式
特点
1.不容易主动攻击,安全性好于ECB,适合传输长度长的报文,是SSL、IPSec的标准。每个密文块依赖于所有的信息块,明文消息中一个改变会影响所有密文块
2.发送方和接收方都需要知道初始化向量
3.加密过程是串行的,无法被并行化
4.在解密时,从两个邻接的密文块中即可得到一个明文块。因此,解密过程可以被并行化
…
…
3、非对称密码
在非对称密码中,加密者与解密者所使用的秘钥并不一样,典型的有RSA加密,椭圆曲线加密
- RSA
- ECC
- …
RSA
RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的绝大多数密码攻击,已被ISO推荐为公钥数据加密标准。
RSA公开密钥密码体制。所谓的公开密钥密码体制就是使用不同的加密密钥不解密密钥,是一种“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制。
基于对极大整数做因数分解的困难性
将两个大质数相乘十分容易,但是想要对其乘积迚行因式分解却极其困难
原理:
①公钥与私钥的产生
- 随机选择两个丌同大质数p和q,计算N=p×q。
- 根据欧拉凼数,求得r=φ(N)=φ§φ(q)=(p−1)(q−1)。
- 选择一个小于r的整数e,使e和r互质。并求得e关于r的模反元素,命名为d(求d令ed≡1(mod r))。
- 将p和q的记录销毁。
此时,(N,e)是公钥,(N,d)是私钥。
②消息加密
将消息m以一个双斱约定好的格式转化为一个小于N且不N互质的整数n迚行加密,消息太长可以分段 ![]()
③消息解密
例题
已知RSA公钥生成参数:
p = 3487583947589437589237958723892346254777
q = 8767867843568934765983476584376578389
e = 65537
求d

攻击
①分解N
在N的比特位数小于512的时候,可以采用大整数分解的策略获叏p和q。
工具:http://factordb.com/ http://souceforge.net/projects/yafu/
②共模攻击
当两个用户使用相同的模数N、不同的私钥时,即存在共模攻击
原理:
设两个用户的公钥分别为e1和e2,且两者互质。明文消息为m,密文分别为:
c1=me1 mod N
c2=me2 mod N
当攻击者截获c1和c2后,就可以恢复出明文。
用扩展欧几里得算法求出re1+se2=1 mod N中的r ,s
得到
c1r×c2s mod N = ((me1 mod N)r×(me2 mod N)s)mod N = ((me1)r×(me2))s) mod N = m(e1^r+e2^s) mod N
e1r+e2s=1
则c1r×c2s mod N =m mod N
③小公钥指数攻击
e特别小,比如e为3
假设用户使用的密钥e=3。考虑到加密关系满足:![]()
攻击者可以从小到大枚举n,依次开三次根,直到开出整数为止
openssl rsa -pubin -in pubkey.pem -text -modulus查看公钥
④低解密指数攻击
低解密指数可以加快解密的过程,但是者也带来了安全问题。Wiener表示如果满足:
那么一种基于连分数(一个数论当中的问题)的特殊攻击类型就可以危害RSA的安全。此时需要满足:
![]()
如果满足上述条件,通过Wiener Attack可以在多项式时间中分解n。
rsa-wiener-attack的攻击源码开源在了github中,采取python编写,可以很容易使用。
识别:
非常简单,e看起来很大就行了。
RSA衍生算法–Rabin算法
Rabin特征在于e=2
Python gmpy库,gmpy.root(a, b),返回一个元组(x, y)
其中x为a开b次方的值,y是判断x是否为整数的布尔型变量。