科学计算三维可视化笔记（第七周 运算）

---

内容来自中国大学MOOC，北京理工大学，python数据分析与展示课程，侵删。
如有错误，烦请指出。

---

科学计算三维可视化笔记 第七周 运算

一、SciPy 介绍

在 Numpy 库的基础上增加了众多的数学、科学以及工程计算中常用的库函数

• 线性代数
• 常微分方程数值求解
• 信号处理
• 图像处理
• 稀疏矩阵

二、SciPy 的常数

SciPy 的 constants 模块包含了众多的物理常数：

三、SciPy 拟合与优化：optimize

optimize 模块提供了许多数值优化算法，可以实现：

• 非线性方程组求解
• 数据拟合
• 函数最小值

1. 非线性方程组求解：fsolve()

fsolve(func, x0)

• func(x) 是计算方程组误差的函数，它的参数 x 是一个矢量，表示方程组的各个未知数的一组可能解，func 返回将 x 代入方程组之后得到的误差
• x0 为未知数矢量的初始值

求解下面的非线性方程组：

• $5x_1+3=0$
• $4x_0^2-2\sin (x_1{x}_2)=0$
• $x_1{x}_2-1.5=0$

2. 最小二乘拟合：leastsq()

leastsq(func, x0)

• func(x) 是计算方程组误差的函数，它使得误差的平方和最小
• x0 为待确定参数的初始值

假设有一组实验数据 $(x_i,y_i)$，他们之间满足函数关系 $f(x)=kx+b$，求解 $k$ 和 $b$ 是多少。

四、SciPy 插值：interpolate

• 插值：通过已知的离散数据来求解未知数据的方法，要求曲线通过所有的已知数据。
• 拟合：要求曲线函数与已知数据集的误差最小，不要求曲线通过所有的已知数据。

intepolate模块提供了许多对数据进行插值运算的函数：

• B 样条曲线插值
• 外推
• Spline 拟合（UnivariateSpline 插值运算）
• 二维插值运算

1. B 样条曲线插值：interp1d()

interp1d(x, y, kind, ...)

• x 和 y 是一系列已知的数据点
• kind 是插值类型，可以是字符串或整数，给出了 B 样条曲线的阶数：
  • zero、nearest：阶梯插值，相当于 0 阶 B 样条曲线
  • slinear、linear：线性插值，相当于 1 阶 B 样条曲线
  • quadratic、cubic：2 阶和 3 阶 B 样条曲线，更高阶的曲线可以直接使用整数值来指定

'''插值：interpolate 之 B样条曲线插值'''
import numpy as np
from scipy import interpolate
import pylab as pl

# 创建数据点集
x = np.linspace(0, 10, 11)
y = np.sin(x)

# 绘制数据点集
pl.plot(x,y,'ro')

# 建立插值数据点
xnew = np.linspace(0, 10, 101)
for kind in ['nearest', 'zero', 'linear', 'quadratic']:
    # 根据kind创建插值对象interp1d
    f = interpolate.interp1d(x, y, kind=kind)
    # 计算插值结果
    ynew = f(xnew)
    # 绘制插值结果
    pl.plot(xnew, ynew, label=str(kind))
pl.legend(loc = 'lower right')
pl.show()

五、SciPy 线性代数：linalg

Numpy 和 SciPy 都提供了线性代数函数库 linalg，SciPy 更为全面：

• 解线性方程组
• 最小二乘解
• 特征值和特征向量
• 奇异值分解

1. 解线性方程组

一个实例：求解$A^{-1}B$，比较两种方法运行时间：

2. 特征值和特征向量

n × n 的矩阵 A 可以看作 n 维空间中的线性变换：

• 如果 x 为 n 维空间中的一个向量，那么 A 与 x 的矩阵乘积是对 x 进行线性变换之后的向量。
• 如果 x 是线性变换的特征向量，那么经过这个线性变换后，得到新向量仍与原来的 x 保持在同一方向上，长度可能发生改变。
• 特征向量的长度在该线性变换下缩放的比例称为其特征值。
• $Ax=\lambda x$

3. 奇异值分解

奇异值分解是线性代数中一种重要的矩阵分解。

• 假设 M 是一个 m × n 阶矩阵，存在一个分解使得 $M=U\Sigma V^{\ast }$
• 其中 U 是 m × m 阶酉矩阵；$\Sigma$ 是半正定 m × n 阶矩阵；$V^{\ast }$ 是 V 的共轭转置，是 n × n 阶酉矩阵
• $\Sigma$ 对角线上的元素为 M 的奇异值，并通常按照从大到小排列

六、SciPy 统计：stats

Stats模块包含了多种概率分布的随机变量，
连续随机变量是 rv_continuous 派生类的对象，
离散随机变量是 rv_discrete 派生类的对象

• 连续概率分布
• 离散概率分布
• 核密度估计
• 二项分布、泊松分布、伽玛分布
• 学生 t - 分布与 t 检验
• 卡方分布和卡方检验

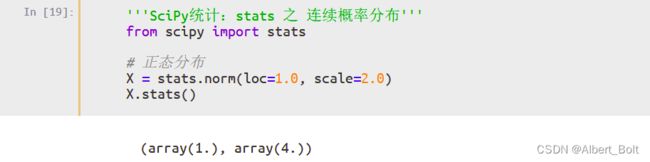
1. 连续概率分布

连续随机变量对象的方法：

2. 离散概率分布

当分布函数的值域为离散时称之为离散概率分布。
stats模块中离散分布随机变量都从 rv_discrete 类继承，也可以直接用 rv_discrete 类自定义离散概率分布。投掷骰子举例：

• 数组 X 保存骰子的所有可能值
• 数组 p 保存每个值出现的概率
• 创建表示这个骰子的随机变量 dic

3. 核密度估计

'''SciPy统计：stats 之 核密度估计'''
from scipy import stats
import numpy as np
import pylab as pl

x = range(1,7)
p = (1.0/6, 1.0/6, 1.0/6, 1.0/6, 1.0/6, 1.0/6)
dice = stats.rv_discrete(values=(x, p))
samples = dice.rvs(size=(20000,50))

# 概率平均值
samples_mean = np.mean(samples, axis=1)

# 核密度估计
_, bins, step = pl.hist(samples_mean, bins=100, density=True, 
                        histtype="step", label="Histogram")
kde = stats.kde.gaussian_kde(samples_mean)
x = np.linspace(bins[0], bins[-1], 100)
pl.plot(x, kde(x), label="kde")

# 拟合正态分布
mean, std = stats.norm.fit(samples_mean)
pl.plot(x, stats.norm(mean,std).pdf(x), alpha=0.8, label="normal fitting")
pl.legend()
pl.show()

七、SciPy 数值积分：integrate

integrate模块提供了几种数值积分算法，包括对常微分方程组（ODE）的数值积分。

• 计算球体体积
• 解常微分方程

1. 球的体积求解

dblquad(func2d, a, b, gfun, hfun)

• func2d：二重积分函数，假定 x，y 是 func3d 的两个参数
• a，b：被积分函数的第一个变量 x 的积分区间
• gfun，hfun：被积分函数第二个变量 y 的积分区间，通过变量 x 计算出变量 y 的积分区间

对于单位球，使用二重积分计算体积：

• 对于 x 轴从 -1 到 1 进行积分
• 对于 y 轴从 -half_circle(x) 到 half_circle(x) 进行积分
• 半球体的二重积分公式为：$V={\int }_{-1}^1{\int }_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}\sqrt{1-x^2-y^2}\mathrm{d}y\mathrm{d}x$

八、SciPy 可视化实例

1. 实例1：mlab 绘制洛伦茨吸引子轨迹

洛伦茨吸引子轨迹的微分方程：



定义函数 lorenz()，计算出某个坐标点在各个方向上的微分值：

'''实例1：洛伦茨因吸引子轨迹'''
from scipy.integrate import odeint
import numpy as np
from mayavi import mlab

# # 给出位置矢量w，和三个参数a, b, c计算出dx/dt, dy/dt, dz/dt的值
def lorenz(w, t, a, b, c):
    x, y, z = w.tolist()
    # 直接与lorenz的计算公式对应
    return np.array([a*(y-x), x*(b-z)-y, x*y-c*z])

# 创建时间点
t = np.arange(0, 30, 0.01)

# 调用ode对lorenz进行求解, 用两个不同的初始值
track1 = odeint(lorenz, (0.0,1.00,0.0), t, args=(10.0,28.0,3.0))
track2 = odeint(lorenz, (0.0,1.01,0.0), t, args=(10.0,28.0,3.0))

# 绘制图形
mlab.plot3d(track1[:,0], track1[:,1], track1[:,2], color=(1,0,0), tube_radius=0.1)
mlab.plot3d(track2[:,0], track2[:,1], track2[:,2], color=(0,0,1), tube_radius=0.1)
mlab.show()

2. 实例2：凸包的二维/三维可视化

• 凸包：指 N 维空间中的一个区域，该区域中任意两点之间的线段都完全被包含在该区域之中
• ConvexHull 可以快速计算包含 N 维空间点的集合的最小凸包

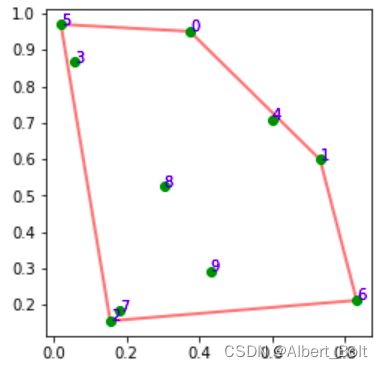
(1) ConvexHull 二维凸包

'''实例2：凸包的二维可视化'''
import numpy as np
from scipy import spatial
import pylab as pl

# 二维平面的随机点
np.random.seed(42)
points2d = np.random.rand(10, 2)

# 点的凸包对象
ch2d = spatial.ConvexHull(points2d)

# 绘制凸包对象
poly = pl.Polygon(points2d[ch2d.vertices], fill=None, lw=2, color='r', alpha=0.5)
ax = pl.subplot(aspect='equal')
pl.plot(points2d[:,0], points2d[:,1], 'go')
for i, pos in enumerate(points2d):
    pl.text(pos[0], pos[1], str(i), color='blue')
ax.add_artist(poly)
pl.show()

(2) ConvexHull 三维凸包
三维空间中的凸包是一个凸多面体，每个面是一个三角形

'''实例2：凸包的三维可视化'''
import numpy as np
from scipy import spatial
from tvtk.api import tvtk
from tvtkfunc import ivtk_scene, event_loop

def convexhull(ch3d):
    # 定义凸多面体tvtk的PolyData()对象
    poly = tvtk.PolyData()
    poly.points = ch3d.points
    poly.polys = ch3d.simplices
    
    # 定义凸多面体定点的小球
    sphere = tvtk.SphereSource(radius=0.02)
    points3d = tvtk.Glyph3D()
    points3d.set_source_connection(sphere.output_port)
    points3d.set_input_data(poly)
    
    # 绘制凸多面体的面，设置半透明度
    m1 = tvtk.PolyDataMapper()
    m1.set_input_data(poly)
    a1 = tvtk.Actor(mapper=m1)
    a1.property.opacity = 0.3
    
    # 绘制凸多面体的边，设置为红色
    m2 = tvtk.PolyDataMapper()
    m2.set_input_data(poly)
    a2 = tvtk.Actor(mapper=m2)
    a2.property.representation = "wireframe"
    a2.property.line_width = 2.0
    a2.property.color = (1.0, 0, 0)
    
    # 绘制凸多面体的顶点，设置为绿色
    m3 = tvtk.PolyDataMapper(input_connection=points3d.output_port)
    a3 = tvtk.Actor(mapper=m3)
    a3.property.color = (0.0, 1.0, 0.0)
    
    return [a1, a2, a3]

# 三维平面的随机点
np.random.seed(42)
points3d = np.random.rand(40, 3)

# 点的凸包对象
ch3d = spatial.ConvexHull(points3d)

# 定义convexhull的Actor
actors=convexhull(ch3d)

# 场景用VTK绘制出来
win = ivtk_scene(actors)
win.scene.isometric_view()
event_loop()