深度优先搜索（DFS）与宽度优先搜索（BFS）解析及例题_c语言

深度优先搜索（DFS）

1.定义

从某个状态开始，不断地转移状态直到无法转移，然后回退到前一步状态，继续转移到其他状态，如此不断重复，直到找到最终的解。
根据深度优先搜索的特点，采用递归函数实现比较简单。
深度优先搜索（隐式地）利用了栈进行计算。

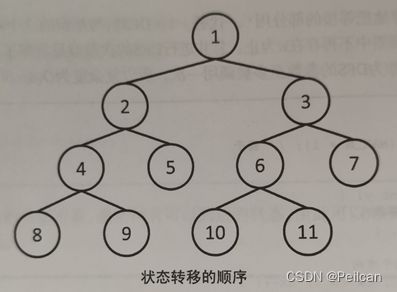
2.状态转移图

3.例题

3.1 部分和问题

问题描述
给定正整数a₁，a₂，…，a_n，判断是否可以从中选出若干数，使他们的和恰好为k。
限制条件

• 1<=n<=20
• -10⁸<=a_i<=10⁸
• -10⁸<=k<=10⁸

样例一
输入：n=4,k=13,a={1,2,4,7}
输出：Yes
解释：13=2+4+7
样例二
输入：n=4,k=15,a={1,2,4,7}
输出：No
分析
从a₁开始按顺序决定每个数加或不加，在全部n个数都决定后再判断它们的和是不是k即可。因为状态数是2ⁿ，所以复杂度为O(2ⁿ)。

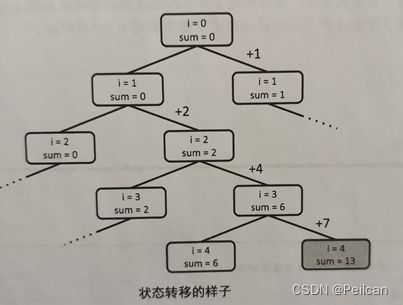
代码

//DFS
#include
#define MAX_N 20
int a[MAX_N]; //存储要求和的数据 
int n,k;      //n代表数据个数，k代表要求出的和
	
//已经从前i项得到了和sum，然后对于i项之后的进行分支 
int dfs(int i, int sum){
	//如果前n项的都经过计算了，如何sum与k相等，返回1，否则返回0
	if(i == n) return sum==k?1:0;
	//不加上a[i]的情况
	if(dfs(i+1, sum)) return 1;
	//加上a[i]的情况
	if(dfs(i+1, sum+a[i])) return 1;
}

int main(){
	scanf("%d %d",&n,&k);
	for(int i=0; i<n; i++) scanf("%d",&a[i]);
	if(dfs(0,0)){
		printf("Yes\n");
	}else{
		printf("No");
	}
}

3.2 Lake Counting

问题描述
有一个大小为N✖N的园子，雨后积起了水。八连通的积水被认为是连接在一起的。请求出园子里总共有多少个水洼？（八连通指的是下图中相对w的*部分）
限制条件

• N，M<=100

样例
输入：N=10，M=12

//园子如下图（'w'表示积水，'.'表示没有积水）
w........ww.
.www.....www
....ww...ww.
.........ww.
.........w..
..w......w..
.w.w.....ww.
w.w.w.....w.
.w.w......w.
..w.......w.

输出：3
分析
从任意的w开始，不停地把邻接的部分用’.‘代替。1次DFS后与初始的这个w所连接的所有w就都被替换成了’.’，因此直到图中不存在w为止，总共进行DFS的次数就是答案。
代码

#include
#define MAX_N 100
#define MAX_M 100
int N,M;
char field[MAX_N][MAX_M];  //园子

//现在位置[x,y] 
void dfs(int x,int y){
	//将现在所在位置替换为.
	field[x][y] = '.';
	
	//循环遍历移动的八个方向
	for(int dx = -1; dx <= 1; dx++){
		for(int dy = -1; dy <= 1; dy++){
			//向x方向移动dx,向y方向移动dy,移动结果为(dx,dy)
			int nx = x + dx, ny = y + dy;
			//判断(nx,ny)是不是在园子内,以及是否有积水
			if(0<=nx && nx<=N && 0<=ny && ny<=M && field[nx][ny]=='w') dfs(nx,ny); 
		}
	}
	return ; 
}

int main(){
	//输入 
	scanf("%d %d",&N,&M);
	getchar();
	for(int i=0; i<N; i++){
		for(int j=0; j<M; j++){
			scanf("%c",&field[i][j]);
		}
		//将第一个for循环后面的换行符去掉，否则scanf默认读取换行符 
		getchar();
	}
	//需要DFS的次数	
	int res = 0;
	//开始dfs
	for(int i=0; i<N; i++){
		for(int j=0; j<M; j++){
			if(field[i][j] == 'w'){
				//从有w的地方开始dfs
				dfs(i,j);
				res++; 
			}
		}
	} 
	printf("%d\n",res);
	return 0;
}

宽度优先搜索（BFS）

1.定义

与深度优先搜索不同之处在于搜索的顺序，宽度优先搜索总是先搜索距离初始状态近的状态。也就是说，它是按照开始状态→只需1次转移就可以到达的所有状态→只需2次就可以到达的所有状态→…这样的顺序进行搜索。对于同一个状态，宽度优先搜索只经过一次，因此时间复杂度为O（状态数✖转移的方式）。
宽度优先搜索利用了队列。搜索时首先将初始状态添加到队列里，此后从队列的最前端不断取出状态，把从该状态可以转换到的状态中尚未访问过的部分加入队列，如此反复，直至队列被取空或找到了问题的解。

2.状态转移图

3.例题

3.1 迷宫的最短路径

问题描述
给定一个大小为N*M的迷宫。迷宫由通道和墙壁组成，每一步可以向邻接的上下左右四格的通道移动。请求出从起点到终点所需的最小步数（起点一定可以到达终点）。
限制条件
N，M<=100
样例
输入：N=10，M=10

//迷宫如下图所示。'#','.','S','G'分别表示墙壁，通道，起点和终点。
#S######.#
......#..#
.#.##.##.#
.#........
##.##.####
....#....#
.#######.#
....#.....
.####.###.
....#...G#

输出：22
分析
宽度优先搜索按照距离开始状态由近及远的顺序进行搜索，因此可以很容易地用来求最短路径、最少操作之类问题的答案。
首先将起点存入队列，然后从队列中取出队头元素，遍历队头元素上下左右四个方向的通道。若其不是终点，则将此点加入队列，并存储从开始到该点的距离。然后处理下一个遍历到的点…直至队列为空。
代码

#include
#define INF 100000000
#define MAX_N 100
#define MAX_M 100
//输入 
char maze[MAX_N][MAX_M+1];  //表示迷宫的字符串的数组 
int N,M;
int sx,sy;  //起点坐标
int gx,gy;  //终点坐标
int d[MAX_N][MAX_M];   //到各个位置的最短距离的数组

//队列存储结构
int queue_x[MAX_N*MAX_M];  //存储进入队列的横坐标 
int queue_y[MAX_N*MAX_M];  //储进入队列的纵坐标 
int front,rear;

//将坐标(x,y)加入队列queue_x,queue_y
void enQueue(int x, int y){
	queue_x[rear++] = x;
	queue_y[rear++] = y;
}

//将横坐标为x的移出queue_x队列 
int deQueue_x(){
	return queue_x[front++];
}

//将纵坐标为y的移出queue_y队列 
int deQueue_y(){
	return queue_y[front++];
}

//求从{sx,sy}到{gx,gy}的最短路径
//如果无法到达，则是INF
void bfs(){
	//初始化
	front = 0;
	rear = 0;
	 
	//当前遍历到的坐标 
	int current_x,current_y;
	
	//把所有的位置都初始化为INF
	for(int i=0; i<N; i++)
		for(int j=0; j<M; j++)
			d[i][j] = INF;
	
	//将起点加入队列，并把这一地点的距离设置为0
	enQueue(sx,sy);
	d[sx][sy] = 0;
	
	//不断循环， 直到队列的长度为0
	while(maze[current_x=deQueue_x()][current_y=deQueue_y()] != 'G'){
		//遍历左右两面 
		for(int dx=-1,dy=0; dx<=1; dx+=2){
			int x = current_x + dx;
			int y = current_y + dy;
			if(x>=0 && x<N && y>=0 && y<M){  //判断未出界 
				if((maze[x][y]=='G' || maze[x][y]=='.') && d[x][y]==INF){
					d[x][y] = d[current_x][current_y] + 1;
					enQueue(x,y);
				}
			}
		}
		//遍历上下两面 
		for(int dy=-1,dx=0; dy<=1; dy+=2){
			int x = current_x + dx;
			int y = current_y + dy;
			if(x>=0 && x<N && y>=0 && y<M){   //判断未出界 
				if((maze[x][y]=='G' || maze[x][y]=='.') && d[x][y]==INF){
					d[x][y] = d[current_x][current_y] + 1;
					enQueue(x,y);
				} 
			}
		}
	} 
} 

int main(){
	scanf("%d %d",&N,&M);
	getchar();
	for(int i=0; i<N; i++){
		for(int j=0; j<M; j++){
			scanf("%c",&maze[i][j]);
			//确定起点坐标 
			if(maze[i][j] == 'S'){
				sx = i;
				sy = j;
			}
			//确定终点坐标
			if(maze[i][j] == 'G'){
				gx = i;
				gy = j;
			} 
		}
		getchar();
	}
	bfs();
	//输出最终结果 
	printf("%d\n",d[gx][gy]);
	return 0;		
}