平衡二叉搜索树(AVL)——【C++实现插入、删除等操作】
本章完整代码gitee地址:平衡二叉搜索树
文章目录
- 0. 前言
- 1. AVL树概念
- 2. 实现AVL树
- 2.1 结构定义
- 2.2 插入
- 左单旋
- 右单旋
- 左右双旋
- 右左双旋
- 2.3 查找
- 2.4 删除
- 2.5 树的高度
- 2.6 是否为平衡树
- 2.7 遍历(中序)
0. 前言
C++的map和set这两个容器的底层就搜索树,关于搜索树,之前此篇文章讲过:数据结构——二叉搜索树,但它可能会出现极端情况:退化为链表
所以再次基础上,就要将这颗树变为平衡的二叉搜索树——ALV树、红黑树,本章讲解的是AVL树
1. AVL树概念
AVL树俄罗斯的两位数学家G.M.Adlson-Velskii和E.M.Landis在1962年发表的论文《An algorithm for the organization of information》公开了这种结构:向二叉树插入一个新节点后,保证每个左右子树的高度之差绝对值不超过1,即可降低树的高度,减少平均搜索的长度。
将左子树减去右子树的深度的值,成为平衡因子BF(Balance Factor),由于绝对值不超过1,则平衡因子的范围是**[-1,1]**,如果超过,就说明目前这棵树不是平衡的,需要进行调整
由于树的左右子树是平衡的,所以要对这棵树操作的时候,最多进行高度次操作:O(lonN)
满二叉树:2h-1 = N
AVL树:2h - X = N(X的范围为[1,2h-1-1]),属于O(lonN),这个量级
2. 实现AVL树
2.1 结构定义
//定义成kv结构
template<class K,class V>
struct AVLTreeNode
{
pair<K, V> _kv;
//三叉链
AVLTreeNode<K, V>* _left; //左节点
AVLTreeNode<K, V>* _right; //右节点
AVLTreeNode<K, V>* _parent; //父亲节点
int _bf; //平衡因子
AVLTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
,_bf(0)
{}
};
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
//功能
private:
}
2.2 插入
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//链接
cur = new Node(kv);
if (parent->_kv.first > kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
//检查
while (parent)
{
//更新平衡因子
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
//判断
if (parent->_bf == 0)
{
//很健康,直接跳出
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
//小问题,无大碍
//继续往上更新
//cur = parent;
parent = parent->_parent;
cur = cur->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
//“生病”了
if (parent->_bf == 2 && cur->_bf == 1) //单纯右高 -- 左单旋
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1) //单纯左高 -- 右单旋
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1) //右子树高,插入点在右子树的左子树引发 -- 右左双旋
{
RotateRL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1) //左子树高,插入点在左子树的右子树引发 -- 左右双旋
{
RotateLR(parent);
}
else
{
assert(false);
}
break;
}
else
{
//防止写的代码有bug
assert(false);
}
}
return true;
}
我们设平衡因子为:右子树-左子树
新增左节点,
parent平衡因子减一新增右节点,
parent平衡因子加一更新后的
parent平衡因子 == 0 ,说明parent所在子树高度不变,无需继续更新祖先节点更新后的
parent平衡因子 == 1 或- 1,说明parent所在子树高度发生变化,影响祖先,需要继续更新祖先节点更新后的
parent平衡因子 == 2 或 -2,说明parent所在子树高度发生变化,且不平衡,需要对parent对所在子树进行旋转,让其平衡这里的平衡因子起到一个检测作用,查看这棵树是否“生病”,如果发现“生病”,立即“治疗”,所以不可能出现大于2的绝对值的平衡因子
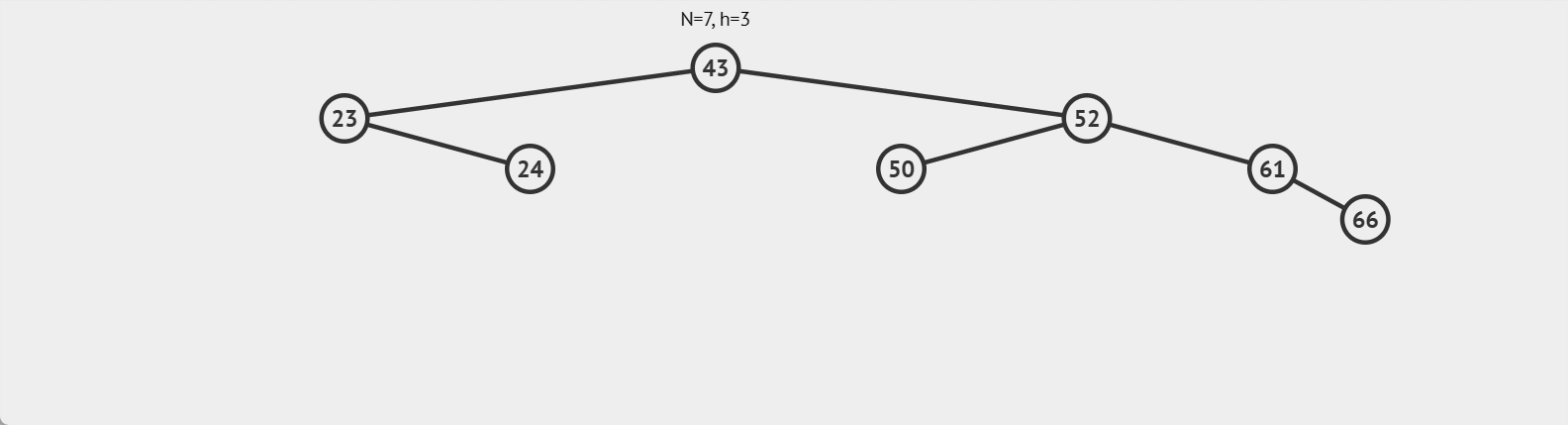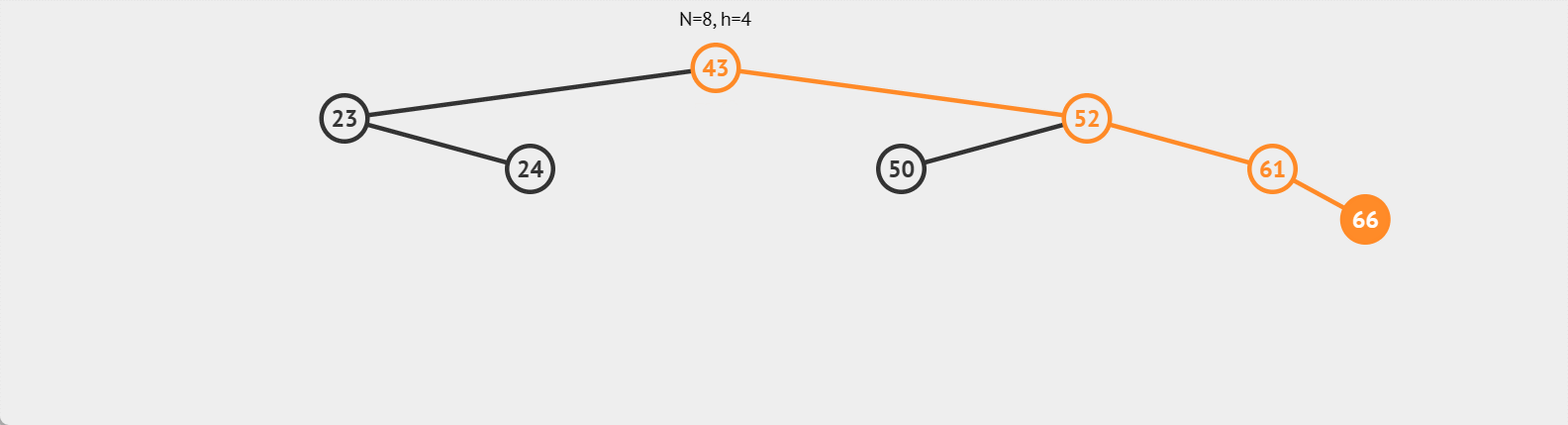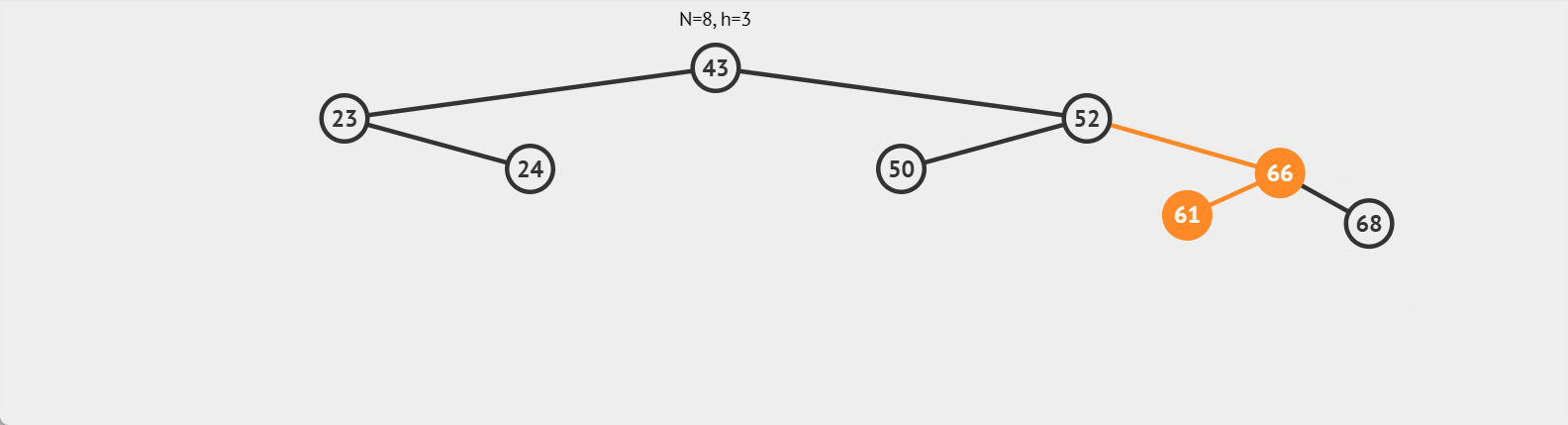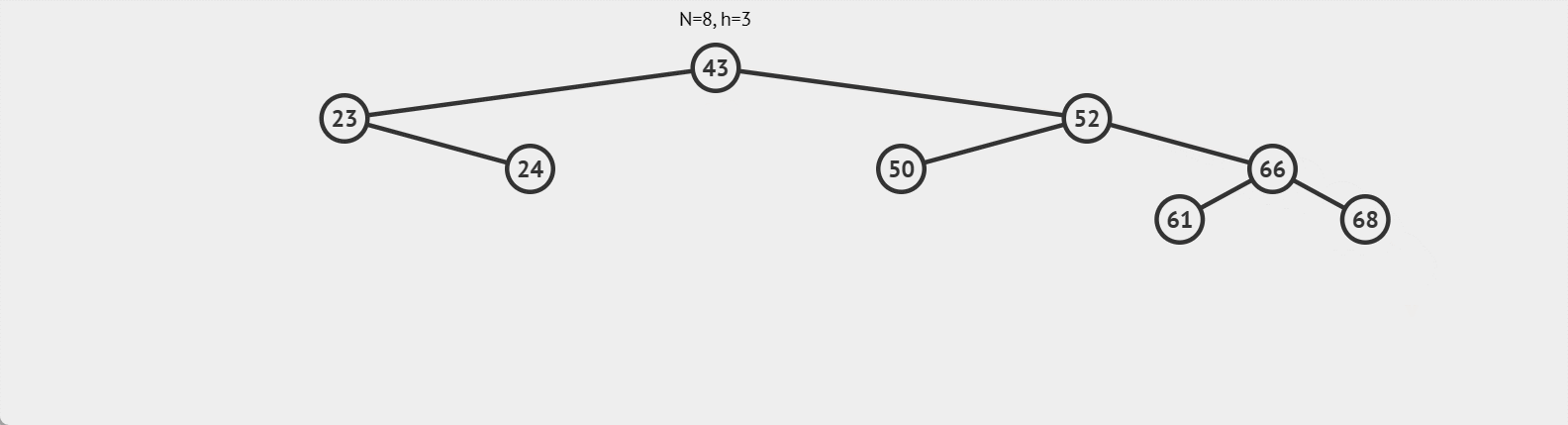
左单旋
单纯右边高,采用左单旋进行调整,具体情况如图:
核心操作:
- `parent->right = cur->left;``
- ``cur->left = parent;`
左单旋实现:
//左单旋
void RotateL(Node* parent)
{
Node* cur = parent->_right;
Node* curleft = cur->_left;
parent->_right = curleft;
if (curleft)
{
curleft->_parent = parent;
}
cur->_left = parent;
Node* ppnode = parent->_parent;
parent->_parent = cur;
if (parent == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
cur->_parent = ppnode;
}
parent->_bf = cur->_bf = 0;
}
动态示例:
右单旋
单纯的左边高,采用右单旋进行调整,具体情况如图:
核心操作:
parent->left = cur->right;cur->right = parent;
右单旋实现:
//右单旋
void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* curRight = cur->_right;
parent->_left = cur->_right;
//防止curRight为空
if (curRight)
{
curRight->_parent = parent;
}
cur->_right = parent;
//保存父亲的父亲节点
Node* ppnode = parent->_parent;
parent->_parent = cur;
if (parent == _root)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
cur->parent = ppnode;
}
//更新平衡因子
parent->_bf = cur->_bf = 0;
}
动图示例:
左右双旋
新插入节点在较高左子树的右侧,采用右左双旋,具体情况如图:
平衡因子更新需要看
cur->right的平衡因子情况:
curRight == 0,它就是插入节点,全部更新为0curRight == 1,c插入,cur->_bf = -1,parent->_bf = 0curRight == -1,b插入,cur->_bf = 0,·parent->_bf = 1`
核心操作:
- 以
parent->left为旋转点左旋 - 以
parent为旋转点右旋 - 根据
curRight->_bf调整平衡因子
右左双旋
新插入节点在较高右子树的左侧,采用右左双旋,具体情况如图:
这里平衡因子的更新,不能和单旋一样直接更新为0,要分情况,我们这里主要是看
cur->left的平衡因子
curLeft->_bf == 0,则它就是插入节点,平衡因子全部更新为0curLeft->_bf == 1,c插入,cur->_bf = 0,parent->_bf = -1curLeft->_bf == -1,b插入,cur->_bf = 1,parent->_bf = 0
核心操作:
- 以为
parent->right为旋转点右旋 - 以
parent为旋转点左旋 - 根据
curLeft->_bf更新平衡因子
右左双旋代码实现:
//右左双旋
void RotateRL(Node* parent)
{
Node* cur = parent->_right;
Node* curLeft = cur->_left;
int bf = curLeft->_bf;
RotateR(parent->_right);
RotateL(parent);
if (bf == 0)
{
//curLeft为新增节点
cur->_bf = 0;
curLeft->_bf = 0;
parent->_bf = 0;
}
else if (bf == 1)
{
//curLeft右子树插入
cur->_bf = 0;
curLeft->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
//curLeft左子树插入
cur->_bf = 1;
curLeft->_bf = 0;
parent->_bf = 0;
}
else
{
assert(false);
}
}
动图示例:
2.3 查找
//查找
Node* Find(const K& key)
{
return _Find(_root, key);
}
因为_root是私有成员,外部无法使用,所以我们设置一个子函数
Node* _Find(Node* root, const K& key)
{
if (root == nullptr || root->_kv.first == key)
return root;
if (root->_kv.first > key)
return _Find(root->_left, key);
else
return _Find(root->_right, key);
}
2.4 删除
删除操作就不多说了,注释写的特别清楚
基本思路就是:
- 删除元素
- 更新平衡因子
与插入类似,但细节还是很多
//删除
bool Erase(const K& key)
{
return _Erase(key);
}
子函数:
bool _Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
//查找元素
while (cur)
{
if (cur->_kv.first > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_kv.first < key)
{
parent = cur;
cur = cur->_right;
}
else
break;
}
//该元素不存在
if (cur == nullptr)
return false;
//删除元素
//1.左右子树都为空
if (cur->_left == nullptr && cur->_right == nullptr)
{
//根节点直接删除退出
if (cur == _root)
{
delete _root;
_root = nullptr;
return true;
}
if (cur == parent->_left)
{
//删除的是左孩子
parent->_bf++;
parent->_left = nullptr;
}
else
{
//删除的是右孩子
parent->_bf--;
parent->_right = nullptr;
}
delete cur;
cur = parent;
}
else if (cur->_left == nullptr) //左子树为空
{
if (cur == _root)
{
_root = cur->_right;
cur->_right->_parent = nullptr;
delete cur;
cur = nullptr;
return true;
}
//因为是平衡二叉树,如果左子树为空,那么右子树至多只有一个节点
//这里前面已经判断了双空的情况,那么肯定右子树只有一个节点,直接删除即可
Node* curRight = cur->_right;
//替换元素
cur->_kv.first = curRight->_kv.first;
cur->_kv.second = curRight->_kv.second;
//删除节点
cur->_right = nullptr;
delete curRight;
curRight = nullptr;
//删右孩子,父节点平衡因子-1
cur->_bf--;
}
else if (cur->_right == nullptr) //右子树为空
{
if (cur == _root)
{
_root = cur->_left;
cur->_left->_parent = nullptr;
delete cur;
cur = nullptr;
return true;
}
//与左子树为空同理
Node* curLeft = cur->_left;
//替换元素
cur->_kv.first = curLeft->_kv.first;
cur->_kv.second = curLeft->_kv.second;
//删除节点
cur->_left = nullptr;
delete curLeft;
curLeft = nullptr;
//删除左孩子,父节点平衡因子+1
cur->_bf++;
}
else
{
//左右子树都不为空
//以左子树最大元素为例
parent = cur; //前驱
Node* prev = cur->_left; //找左子树最大元素
while (prev->_right)
{
parent = prev;
prev = prev->_right;
}
//替换元素
cur->_kv.first = prev->_kv.first;
cur->_kv.second = prev->_kv.second;
//右边肯定没有元素了,因为找的就是最大的元素:左子树里面的最右边
if (parent->_left == prev)
{
parent->_left = prev->_left;
parent->_bf++;
}
else
{
parent->_right = prev->_left;
parent->_bf--;
}
delete prev;
prev = nullptr;
//指向删除节点父亲
cur = parent;
}
parent = cur->_parent;
//重新找调整位置
if (cur->_bf == -2 || cur->_bf == 2)
{
if (cur->_bf == -2)
{
Node* curLeft = cur->_left;
parent = cur;
cur = curLeft;
}
else
{
Node* curRight = cur->_right;
parent = cur;
cur = curRight;
}
}
//if (cur->_bf == 0 && parent != nullptr && abs(parent->_bf) == 2)
//{
// if (cur = parent->_left)
// cur = parent->_right;
// else
// cur = parent->_left;
//}
while (parent)
{
//更新父亲的平衡因子
parent->_bf = UpdateBf(parent);
if (parent->_bf == 2 || parent->_bf == -2)
{
//“生病”了
if (parent->_bf == 2 && cur->_bf == 1) //单纯右高 -- 左单旋
{
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1) //单纯左高 -- 右单旋
{
RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1) //右子树高,插入点在右子树的左子树引发 -- 右左双旋
{
RotateRL(parent);
}
else if (parent->_bf == 2 && cur->_bf == 1) //左子树高,插入点在左子树的右子树引发 -- 左右双旋
{
RotateLR(parent);
}
else if (parent->_bf == 2)
{
//cur->_bf == 0时
RotateL(parent);
//再更新一次
parent->_bf = UpdateBf(parent);
}
else if (parent->_bf == -2)
{
RotateR(parent);
parent->_bf = UpdateBf(parent);
}
else
{
assert(false);
}
}
cur = parent;
parent = cur->_parent;
}
return true;
}
int UpdateBf(Node* root)
{
if (!root)
return 0;
int leftH = _Height(root->_left);
int rightH = _Height(root->_right);
return rightH - leftH;
}
2.5 树的高度
int _Height(Node* root)
{
if (root == nullptr)
return 0;
//记录深度
int leftH = _Height(root->_left);
int rightH = _Height(root->_right);
//记录更深的那一个
return std::max(leftH, rightH) + 1;
}
2.6 是否为平衡树
bool _IsAVLTree(Node* root)
{
//空树符合AVL树
if (root == nullptr)
return true;
//左子树的高度
int leftH = _Height(root->_left);
//右子树高度
int rightH = _Height(root->_right);
//看平衡因子是否符合
int bf = rightH - leftH;
if (bf != root->_bf)
return false;
//平衡因子绝对值不大于
//在一次递归左右子树
return abs(bf) < 2 && _IsAVLTree(root->_left) && _IsAVLTree(root->_right);
}
2.7 遍历(中序)
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_kv.first << " ";
_InOrder(root->_right);
}
那本次分享就到这里咯,AVL树主要是重点了解其中是如何变平衡的(各种旋转),在实际中,我们只有使用C++里面的map和set(底层是红黑树)。
我们下期再见咯,如果还有下期的话。
Tips:
如果代码有bug,希望大家能指出来,看了网上好多的都有bug
不知道这个有没有bug,我测了一些数据,目前没发现bug