2023秋招人均手撕的跳表,你还不会?【力扣跳表实现】
2023秋招人均手撕的跳表,你还不会?【力扣跳表实现】
最近听到同学在面试实习时遇到了面试官让手撕跳表。而我对跳表也只是了解的水平,于是这两天学习了一下。
跳表是什么
跳表是一种数据结构。它使得包含n个元素的有序序列的查找和插入操作的平均时间复杂度都是O(logn)。这个时间复杂度与红黑树相等,但是跳表的实现要比红黑树简单!
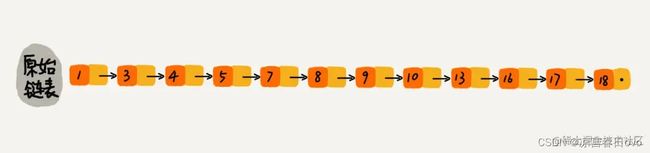
如下图是一个具有n个节点的有序单链表。如果想要从链表中找到10这个元素,只能从头开始遍历链表,时间复杂度是O(n)。
为了提高查找效率,可以把链表中每两个元素抽出来加一级索引,一级索引向下指向原始链表的对应节点,如下图。这时如果要查找10这个元素,该如何查找呢?索引节点相当于将n个节点每两个一份分成了n/2份,我们先找到10这个节点在哪一份,然后再在这一份中查找。具体来说,在以及索引中遍历1,4,7,9,遍历到9时发现9的后继节点13比10大。于是我们就可以确定,10在9和13之间。于是可以向下移动到原始链表,然后往后遍历查找到10.
加了一级索引后,查找效率有所提升。进一步我们可以添加二级索引,如下图。这时,查找10的过程为,在二级索引上遍历1,7,发现下一个节点13比10大,向下移动至一级索引,遍历7,9,发现下个节点13比10大。向下移动至原始链表,然后找到10.发现查找的效率更高了。跳表的思想就是通过加索引来加快查找速度,空间换时间。
综上,跳表是通过添加索引,实现二分查找的有序链表。
查找的时间复杂度
跳表查找一个元素是从最高层索引开始,逐层遍历直到原始链表。因此时间复杂度 = 索引高度 * 每层索引遍历元素的个数。
跳表索引的高度 h = log2n。如下图,原始的链表有n个元素,则一级索引有n/2个元素,二级索引有n/4个元素,第k级索引就有n/2k个元素。而最高级索引一般有2个元素,最高级索引2 = n/2h,可以得到h=log2n - 1,最高级索引 h 为索引的高度加上原始链表的一层,跳表的总高度为 h = log2n
当每 2 个元素抽出一个节点作为上层索引的节点时,每一层最多遍历 3 个元素。跳表的索引高度 h = log2n,且每层索引最多遍历 3 个元素。所以跳表中查找一个元素的时间复杂度为O(3log2n),省略常数即:O(logn)。
空间复杂度
设原始链表包含 n 个元素,则一级索引元素的个数为 n/2、二级索引元素个数为 n/4…所以,索引节点综合为: n/2 + n/4 + n/8 + … + 2 = n - 2,空间复杂度为 O(n)。
这个式子可以看作是a0=2, q = 2,元素个数为h = log2n - 1 的等比数列,利用等比数列求和公式Sn = a0 (1-qr) / (1-q),代入得到
n - 2
如果每 3 个节点抽一个节点作为索引,索引总和数就是 n/3 + n/9 + n/27 + … + 9 + 3 + 1 = (n-1)/2 查询的空间复杂度为 O(4log3n)。可以看到如果抽取的间隔节点数,空间有所节省但查找效率也有一定的下降。
索引节点往往只需要存储 key 和几个指针,并不需要存储完整的对象,所以当对象比索引节点大很多时,索引占用的额外空间就可以忽略了。
插入数据
随机得到插入节点的层数。为了在插入数据的同时维护索引节点,可以采用随机化的方法得到插入节点的最高层级,然后小于这个层级的每个层级都应该插入该节点。
我们可以认为,当原始链表中元素数量足够大,且抽取足够随机的话,我们得到的索引是均匀的。其效率与上述提到的每几个元素抽取一个作为上层索引节点的做法可以认为是几乎相等的。因此,我们可以维护这样一个索引:随机选取 n/2 个元素作为一级索引,随机选取 n/4 个元素作为二级索引、随机选取 n/8 个元素作为三级索引。
具体来说,每次我们要插入一个节点,让该节点有 1/2 的几率建立一级索引,1/4 的几率建立二级索引,1/8的几率建立三级索引。下面的randomLevel()方法,有1/2的概率返回1,1/4的概率返回2,1/8的概率返回3.
randomLevel()返回 1 表示插入的当前元素不需要建索引,
randomLevel()返回 2 表示插入的元素需要建立一级索引
randomLevel()返回 3 表示插入的元素需要建立二级索引
// FACTOR 是生成索引的概率 0.5 或 0.25等
// MAX_LEVEL 是跳表的最大层级
private int randomLevel() {
int lv = 1;
while(random.nextDouble() < FACTOR && lv < MAX_LEVEL) {
lv ++;
}
return lv;
}
删除数据和插入数据的思路类似,都需要先查找到新元素插入的位置,或者找到要删除的数据的位置。然后进行添加或者删除就好了,时间复杂度是查找的时间复杂度 + 添加或删除需要的时间复杂度(也是logn),因此总的时间复杂度还是logn。
这里我们直接上代码了:
力扣 1206 设计跳表
下面代码中FACTOR是每个节点成为上层索引节点的概率。MAX_LEVEL是跳表的最大层级,这个层级包含原始链表。这里设置的FACOR = 0.25,MAX_LEVEL = 32,可以容纳的节点为431,这个数字大概是4×1018次方的数量级。
ok,接下来具体解释一下每段代码的具体含义:
下面这段代码定义了跳表的节点。可以看到一个节点有一个值val和一个指针数组next,这个指针数组对应的就是每个层级的指针,next[0]指向第0层该节点的下一个节点。
class SkipListNode {
int val;
SkipListNode[] next;
SkipListNode(int _val, int maxLevel) {
this.val = _val;
this.next = new SkipListNode[maxLevel];
}
}
然后是关于跳表参数的定义。FACTOR和MAX_LEVEL已经说过了。head是跳表的头(需要定义一个MAX_LEVEL的指针数组,这样才能通过head访问每个层级),level是跳表的层数。
// 跳表参数定义
private static final double FACTOR = 0.25D;
private static final int MAX_LEVEL = 32;
private SkipListNode head; // 哨兵节点
private int level; // 跳表的层数
private Random random;
public Skiplist() {
this.head = new SkipListNode(-1, MAX_LEVEL);
this.level = 0;
this.random = new Random();
}
search()方法的实现思路。从最顶层level开始逐层遍历,当下一个节点为null,或者下一个节点的值大于等于要找的target,说明要找的值在cur和cur.next[i]之间,就可以移动至下一层级。这里的i代表的就是当前搜索的层级。在遍历到第 0 层,通过判断下一个节点是否是要找的target来判断跳表中是否存在值为target的节点。通过以上逻辑可以判断,如果存在值相同的多个元素,跳表找到的是第一个元素。
public boolean search(int target) {
// search 的逻辑
SkipListNode cur = head;
for(int i = level - 1;i >= 0;i --) {
while(cur.next[i] != null && cur.next[i].val < target) {
cur = cur.next[i];
}
// 移动到下一层,同一个节点因此不用操作
}
// 遍历到第 1 层,查看下一个节点是否是 target
if(cur.next[0] != null && cur.next[0].val == target) {
return true;
}
return false;
}
add()方法的思路。同样是从level层开始遍历,为了便于添加节点,需要在遍历到每一层最后一个节点时,用update数组记录该节点。update数组初始化为head节点(当新加入的节点的层级大于跳表的层级level时便于插入)。随机一个层级lv,更新跳表的层级取max(level,lv)。新节点的next数组的大小可以设置成lv。最后,就可以通过update数组在[0, lv - 1]的每一层遍历的最后一个节点后面添加新节点。
public void add(int num) {
// 从最高层开始遍历
// update 数组保存每一层遍历的最后一个节点
SkipListNode[] update = new SkipListNode[MAX_LEVEL];
// 将 update 数组初始化成 head 便于后续处理
// 新增节点随机得到的层数有可能 > 当前 level
Arrays.fill(update, head);
SkipListNode cur = head;
// 这里 i 就表示 cur 当前遍历的层级
for(int i = level - 1;i >= 0;i --) {
while(cur.next[i] != null && cur.next[i].val < num) {
cur = cur.next[i];
}
// 记录每一层访问的最后一个节点
update[i] = cur;
// 移动到下一层
}
// 需要确定新增节点所处的层级
// 有 p 的概率位于第 2 层
// 有 p^(i-1) 的概率位于第 i 层 ...
int lv = randomLevel();
// 添加完成后需要更新跳表层级
level = Math.max(level, lv);
SkipListNode newNode = new SkipListNode(num, lv); // 这里 next 可以只有 lv大小
// 利用 update 数组向每个层级的对应位置添加元素
for(int i = 0;i < lv;i ++) {
newNode.next[i] = update[i].next[i];
update[i].next[i] = newNode;
}
}
随机层级的函数。默认层级为 1,有 FACTOR 的概率层级为大于等于 2,也就是有FACTOR的概率建立一级索引。
private int randomLevel() {
int lv = 1;
while(random.nextDouble() < FACTOR && lv < MAX_LEVEL) {
lv ++;
}
return lv;
}
earse()方法的思路。同样是先逐层遍历跳表,用update数组记录每层遍历的最后一个节点。通过判断第 0 层的遍历的最后一个节点的下一个节点是否是num来判断要删除的元素是否存在。如果存在,从 0 层开始向上删除该节点,直到该节点不存在为止。
public boolean erase(int num) {
// 需要判断 num 在跳表中是否存在
// 存在才能进行删除
// 由于每个层级 num 节点的前驱节点不一定相同,需要使用 update 数组进行记录
SkipListNode[] update = new SkipListNode[level];
Arrays.fill(update, head);
SkipListNode cur = head;
for(int i = level - 1;i >= 0;i --) {
while(cur.next[i] != null && cur.next[i].val < num) {
cur = cur.next[i];
}
update[i] = cur;
// 移动到下个层级
}
if(cur.next[0] == null || cur.next[0].val != num) {
// num 在跳表中不存在
return false;
}
// num 在跳表中存在需要删除
for(int i = 0;i < level;i ++) {
if(update[i].next[i] == null || update[i].next[i].val != num) {
break;
}
update[i].next[i] = update[i].next[i].next[i];
}
// 删除后,需要更新跳表的层级
while(level > 1 && head.next[level-1] == null) {
level --;
}
return true;
}
下面是跳表的完整代码。
class SkipListNode {
int val;
SkipListNode[] next;
SkipListNode(int _val, int maxLevel) {
this.val = _val;
this.next = new SkipListNode[maxLevel];
}
}
class Skiplist {
// 跳表参数定义
private static final double FACTOR = 0.25D;
private static final int MAX_LEVEL = 32;
private SkipListNode head; // 哨兵节点
private int level; // 跳表的层数
private Random random;
public Skiplist() {
this.head = new SkipListNode(-1, MAX_LEVEL);
this.level = 0;
this.random = new Random();
}
public boolean search(int target) {
// search 的逻辑
SkipListNode cur = head;
for(int i = level - 1;i >= 0;i --) {
while(cur.next[i] != null && cur.next[i].val < target) {
cur = cur.next[i];
}
// 移动到下一层,同一个节点因此不用操作
}
// 遍历到第 1 层,查看下一个节点是否是 target
if(cur.next[0] != null && cur.next[0].val == target) {
return true;
}
return false;
}
public void add(int num) {
// 从最高层开始遍历
// update 数组保存每一层遍历的最后一个节点
SkipListNode[] update = new SkipListNode[MAX_LEVEL];
// 将 update 数组初始化成 head 便于后续处理
// 新增节点随机得到的层数有可能 > 当前 level
Arrays.fill(update, head);
SkipListNode cur = head;
// 这里 i 就表示 cur 当前遍历的层级
for(int i = level - 1;i >= 0;i --) {
while(cur.next[i] != null && cur.next[i].val < num) {
cur = cur.next[i];
}
// 记录每一层访问的最后一个节点
update[i] = cur;
// 移动到下一层
}
// 需要确定新增节点所处的层级
// 有 p 的概率位于第 2 层
// 有 p^(i-1) 的概率位于第 i 层 ...
int lv = randomLevel();
// 添加完成后需要更新跳表层级
level = Math.max(level, lv);
SkipListNode newNode = new SkipListNode(num, lv); // 这里 next 可以只有 lv大小
// 利用 update 数组向每个层级的对应位置添加元素
for(int i = 0;i < lv;i ++) {
newNode.next[i] = update[i].next[i];
update[i].next[i] = newNode;
}
}
private int randomLevel() {
int lv = 1;
while(random.nextDouble() < FACTOR && lv < MAX_LEVEL) {
lv ++;
}
return lv;
}
public boolean erase(int num) {
// 需要判断 num 在跳表中是否存在
// 存在才能进行删除
// 由于每个层级 num 节点的前驱节点不一定相同,需要使用 update 数组进行记录
SkipListNode[] update = new SkipListNode[level];
Arrays.fill(update, head);
SkipListNode cur = head;
for(int i = level - 1;i >= 0;i --) {
while(cur.next[i] != null && cur.next[i].val < num) {
cur = cur.next[i];
}
update[i] = cur;
// 移动到下个层级
}
if(cur.next[0] == null || cur.next[0].val != num) {
// num 在跳表中不存在
return false;
}
// num 在跳表中存在需要删除
for(int i = 0;i < level;i ++) {
if(update[i].next[i] == null || update[i].next[i].val != num) {
break;
}
update[i].next[i] = update[i].next[i].next[i];
}
// 删除后,需要更新跳表的层级
while(level > 1 && head.next[level-1] == null) {
level --;
}
return true;
}
}
/**
* Your Skiplist object will be instantiated and called as such:
* Skiplist obj = new Skiplist();
* boolean param_1 = obj.search(target);
* obj.add(num);
* boolean param_3 = obj.erase(num);
*/
参考资料:https://juejin.cn/post/6844903955831619597