对偶转化和非线性规划
对偶理论
- 对偶转化和非线性规划
-
- 对称形式
- 非对称形式
- 非线性规划
-
- 凸函数
- 无约束问题的最优解
对偶转化和非线性规划
对称形式
推 导 公 式 如 下 ： 推导公式如下： 推导公式如下：
m a x Z = C T x 转 化 为 ⟹ m i n W = Y T b maxZ=C^Tx 转化为\implies minW=Y^Tb maxZ=CTx转化为⟹minW=YTb
s t : { A x ≤ b x ≥ 0 转 化 为 ⟹ s t : { A T y ≤ b y ≥ 0 st:\begin{cases} Ax\le b\\ x\ge0 \end{cases}转化为\implies st:\begin{cases} A^Ty\le b\\ y\ge0 \end{cases} st:{Ax≤bx≥0转化为⟹st:{ATy≤by≥0
例子1：写出下列问题的对偶规划
m a x Z = 5 x 1 + 6 x 2 \color{maroon}max Z=\color{red}{5}\color{black}x_1+\color{red}{6}\color{black}x_2 maxZ=5x1+6x2
s t : { 3 x 1 − 2 x 2 ≤ 7 4 x 1 + 1 x 2 ≤ 9 x 1 , x 2 ≥ 0 st:\begin{cases} \color{lime}3\color{black}x_1-\color{purple}2\color{black}x_2\le\color{#00ff00}{7} \\ \color{lime}4\color{black}x_1+\color{purple}1\color{black}x_2\le\color{#00ff00}{9}\\ x_1,x_2\color{olive}\ge0 \end{cases} st:⎩⎪⎨⎪⎧3x1−2x2≤74x1+1x2≤9x1,x2≥0
对 偶 规 划 为 ： m i n W = 7 y 1 + 9 y 2 对偶规划为：\color{maroon}min W=\color{#00ff00}{7}\color{black}{y_1}+\color{#00ff00}{9}\color{black}{y_2} 对偶规划为：minW=7y1+9y2
s t : { 3 y 1 + 4 y 2 ≥ 5 − 2 y 1 + 1 y 2 ≥ 6 y 1 , y 2 ≥ 0 st:\begin{cases} \color{lime}3\color{black}y_1+\color{lime}4\color{black}y_2\ge\color{red}{5} \\ \color{purple}-2\color{black}y_1+\color{purple}1\color{black}y_2\ge\color{red}{6}\\ y_1,y_2\color{olive}\ge0 \end{cases} st:⎩⎪⎨⎪⎧3y1+4y2≥5−2y1+1y2≥6y1,y2≥0
非对称形式
列 1 ： 转 化 下 面 的 非 对 称 形 式 的 对 偶 规 划 列1：转化下面的非对称形式的对偶规划 列1：转化下面的非对称形式的对偶规划
m i n Z = 2 x 1 + 3 x 2 − 5 x 3 + x 4 minZ=2x_1+3x_2-5x_3+x_4 minZ=2x1+3x2−5x3+x4
s t : { 2 x 1 + x 2 − 3 x 3 + x 4 ≥ 5 2 x 1 + x 3 − x 4 ≤ 4 x 2 + x 3 + x 4 = 6 x 1 ≤ 0 , x 2 , x 3 ≥ 0 , x 4 无 约 束 st:\begin{cases} \color{red}2x_1+x_2-3x_3+x_4\ge5\\ \color{red}2x_1+x_3-x_4\le4\\ \color{red}x_2+x_3+x_4=6\\ \color{blue}x_1\le0,x_2,x_3\ge0,x_4无约束 \end{cases} st:⎩⎪⎪⎪⎨⎪⎪⎪⎧2x1+x2−3x3+x4≥52x1+x3−x4≤4x2+x3+x4=6x1≤0,x2,x3≥0,x4无约束
解 ： 对 偶 规 划 如 下 解：对偶规划如下 解：对偶规划如下
m a x W = 5 y 1 + 4 y 2 + 6 y 3 maxW=5y_1+4y_2+6y_3 maxW=5y1+4y2+6y3
s t : { 2 y 1 + 2 y 2 ≥ 2 y 1 + y 3 ≤ 4 − 3 y 1 + y 2 + y 3 ≤ 5 y 1 − y 2 + y 3 = 1 y 1 ≥ 0 , y 2 ≤ 0 , y 3 无 约 束 st:\begin{cases} \color{blue}2y_1+2y_2\ge2\\ \color{blue}y_1+y_3\le4\\ \color{blue}-3y_1+y_2+y_3\le5\\ \color{blue}y_1-y_2+y_3=1\\ \color{red}y_1\ge0,y_2\le0,y_3无约束 \end{cases} st:⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧2y1+2y2≥2y1+y3≤4−3y1+y2+y3≤5y1−y2+y3=1y1≥0,y2≤0,y3无约束
上面由min推max，此时先看 蓝 色 部 分 \color{blue}蓝色部分 蓝色部分，由min的变量约束推导max的4个约束条件， 符 号 相 反 \color{blue}符号相反 符号相反，无约束的时候去等号。
再看 红 色 部 分 \color{red}红色部分 红色部分，由min的三个约束条件，推导max的变量约束， 符 号 相 同 ， \color{red}符号相同， 符号相同，取等号的时候变量无约束。
非线性规划
凸函数
定 义 ： S 是 R n 的 非 空 集 合 ， f 是 定 义 在 S 上 的 实 函 数 ， 若 任 取 S 中 的 两 点 定义：S是R^n的非空集合，f是定义在S上的实函数，若任取S中的两点 定义：S是Rn的非空集合，f是定义在S上的实函数，若任取S中的两点
x 1 , x 2 及 任 意 实 数 ⋋ ∈ ( 0 , 1 ) 都 有 ： x_1,x_2及任意实数⋋\in(0,1)都有： x1,x2及任意实数⋋∈(0,1)都有：
f ( ⋋ x 1 + ( 1 − ⋋ ) x 2 ) ≤ ⋋ f ( x 1 ) + ( 1 − ⋋ ) f ( x 2 ) f(⋋x_1+(1-⋋)x_2)\le⋋f(x_1)+(1-⋋)f(x_2) f(⋋x1+(1−⋋)x2)≤⋋f(x1)+(1−⋋)f(x2)
其中 ⋋ x 1 + ( 1 − ⋋ ) x 2 表 示 x 1 , x 2 ⋋x_1+(1-⋋)x_2表示x_1,x_2 ⋋x1+(1−⋋)x2表示x1,x2两点之间连线上的一点，画出示意图如下
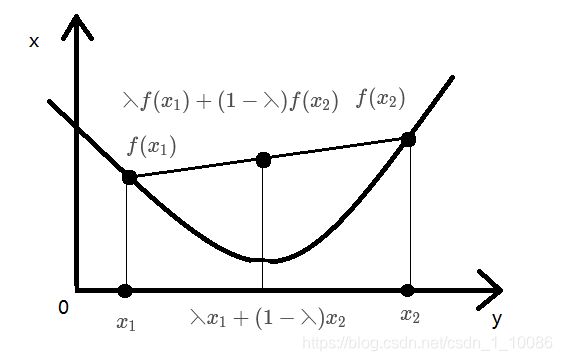严格凸函数指的是 f ( ⋋ x 1 + ( 1 − ⋋ ) x 2 ) < ⋋ f ( x 1 ) + ( 1 − ⋋ ) f ( x 2 ) f(⋋x_1+(1-⋋)x_2)\lt⋋f(x_1)+(1-⋋)f(x_2) f(⋋x1+(1−⋋)x2)<⋋f(x1)+(1−⋋)f(x2)不取等号
{ 凸 函 数 ⟹ ∇ 2 f ( x ) 半 正 定 严 格 凸 函 数 ⟹ ∇ 2 f ( x ) 正 定 { ⋋ ( 特 征 值 ) > 0 ∇ 2 f ( x ) 是 对 称 阵 添 加 知 识 点 { ∣ ⋋ E n − A ∣ = 0 求 特 征 值 A 正 定 ⟺ A 的 各 阶 顺 序 主 子 式 大 于 0 \begin{cases} 凸函数\implies \nabla^2f(x)半正定\\ 严格凸函数\implies \nabla^2f(x)正定\begin{cases} ⋋(特征值)\gt0\\ \nabla^2f(x)是对称阵\\ \end{cases}\\ 添加知识点\begin{cases} |⋋E_n-A|=0求特征值\\ A正定\iff A的各阶顺序主子式大于0\\ \end{cases}\\ \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧凸函数⟹∇2f(x)半正定严格凸函数⟹∇2f(x)正定{⋋(特征值)>0∇2f(x)是对称阵添加知识点{∣⋋En−A∣=0求特征值A正定⟺A的各阶顺序主子式大于0
无约束问题的最优解
{ x ∗ 是 局 部 最 优 解 − > ∇ f ( x ∗ ) = 0 , 并 且 ∇ 2 f ( x ∗ ) 是 半 正 定 矩 阵 ∇ f ( x ∗ ) = 0 , 并 且 ∇ 2 f ( x ∗ ) 是 正 定 矩 阵 − > x ∗ 是 局 部 最 优 解 \begin{cases} x^*是局部最优解->\nabla f(x^*)=0,并且\nabla^2f(x^*)是半正定矩阵\\ \nabla f(x^*)=0,并且\nabla^2f(x^*)是正定矩阵->x^*是局部最优解 \\ \end{cases} {x∗是局部最优解−>∇f(x∗)=0,并且∇2f(x∗)是半正定矩阵∇f(x∗)=0,并且∇2f(x∗)是正定矩阵−>x∗是局部最优解
列题1：求下面非线性规划问题
m i n f ( x 1 , x 2 , x 3 ) = x 1 2 + 4 x 2 2 + x 3 2 − 2 x 1 minf(x_1,x_2,x_3)=x_1^2+4x_2^2+x_3^2-2x_1 minf(x1,x2,x3)=x12+4x22+x32−2x1
解 ： ∇ f ( x 1 , x 2 , x 3 ) = ( 2 x 1 , 8 x 2 , 2 x 3 ) = ( 0 , 0 , 0 ) 解：\nabla f(x_1,x_2,x_3)=(2x_1,8x_2,2x_3)=(0,0,0) 解：∇f(x1,x2,x3)=(2x1,8x2,2x3)=(0,0,0)
求 得 x 1 = 1 , x 2 = x 3 = 0 求得x_1=1,x_2=x_3=0 求得x1=1,x2=x3=0
分 别 对 x 1 , x 2 , x 3 求 导 得 到 ∇ 2 f ( x 1 , x 2 , x 3 ) [ 2 0 0 0 8 0 0 0 2 ] 分别对x_1,x_2,x_3求导得到\nabla^2 f(x_1,x_2,x_3) \left[ \begin{array}{cc} 2&0&0\\ 0&8&0\\ 0&0&2 \end{array} \right] 分别对x1,x2,x3求导得到∇2f(x1,x2,x3)⎣⎡200080002⎦⎤
∇ 2 f ( x 1 , x 2 , x 3 ) 对 称 ， ⋋ 1 = 2 , ⋋ 2 = 8 , ⋋ 3 = 2 , 是 正 定 的 ， 于 是 解 x ∗ = ( 1 , 0 , 0 ) \nabla^2 f(x_1,x_2,x_3)对称，⋋_1=2,⋋_2=8,⋋_3=2,是正定的，于是解x^*=(1,0,0) ∇2f(x1,x2,x3)对称，⋋1=2,⋋2=8,⋋3=2,是正定的，于是解x∗=(1,0,0)