二叉树的顺序结构以及堆的实现——【数据结构】

W...Y的主页 

代码仓库分享  

---

上篇文章，我们认识了什么是树以及二叉树的基本内容、表示方法……接下来我们继续来深入二叉树，感受其中的魅力。

目录

 二叉树的顺序结构

堆的概念及结构

堆的实现  

堆的创建 

堆的初始化与释放空间 

堆的插入

堆的删除

 堆实现的代码接口，以及简单函数的直接实现

---

 二叉树的顺序结构

普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。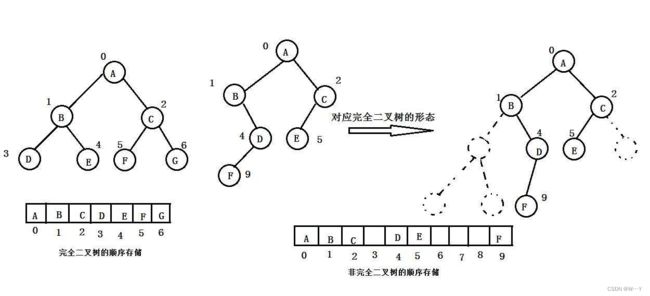

 顺序存储又叫数组存储，是指一层一层存入数组中去。物理层面上是一个数组，在逻辑上面是一个二叉树！！！

而在顺序存储中有一些规律：

通过父节点可以找到自己左右两个孩子：

左孩子：leftchild = parent*2+1;

右孩子：rightchild = parent*2+2; 

通过孩子节点可以找到父节点：

parent = (child-1)/2;

因为我们将数据按照二叉树的规律存入数组中（从上到下、从左往右）所以父节点与子节点就有一些特殊的规律，这个是我们经常会用到的，需要我们熟记于心！！！

总结：如果强行将一个普通的二叉树用数组存储，会浪费许多空间。所以只有满二叉树与完全二叉树才可以进行数组顺序存储。 

堆的概念及结构

这个堆与操作系统中的堆不同，操作系统将内存存储划分为栈区、堆区、静态区……而这个堆是一种数据结构。 

堆的概念：

如果有一个关键码的集合K = {k0 ，k1 ，k2 ，…，kn-1 }，把它的所有元素按完全二叉树的顺序存储方式存储
在一个一维数组中，并满足：  ki<=k(2*i+1) 且ki <=k(2*i+2) ( ki>=k(2*i+1) 且 ki>=k(2*i+2)) i = 0,1,2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。（以上k后面的数字以及表达式全部为角标i）
堆的性质：
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。 

小堆：树中任何一个父亲的值都<=孩子的值

大堆：树中任何一个父亲的值都>=孩子的值

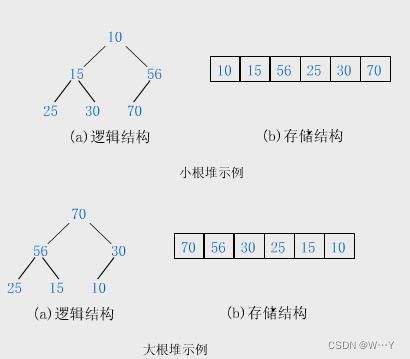
小堆那堆的底层数组是否为升序呢？ 

不一定！

这个堆转换成数组为：10 15 56 25 30 70明显不是升序，堆只能保证父亲小于(大于)孩子，并不是与堂兄第比较。但是我们可以发现小堆的根是整棵树中最小值。

所以我们可以利用发现解决topk问题与堆排序。

堆排序是非常快的，时间复杂度只有O(N*logN)

堆的实现  

堆的创建 

想要实现堆，我们先来表示堆，堆的创建其实就与顺序表大同小异，因为在物理层面上就是一个数组。

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

创建指针指向将要动态开辟的数组中，size记录有效存储数据个数，capacity记录开辟空间大小。

堆的初始化与释放空间 

还是与顺序表相同，我们将堆中指针置空，size与capacity赋值0即可。

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

 释放空间也非常简单，free掉开辟的空间，指针置空，size与capacity赋值0即可。

void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->size = php->capacity = 0;
}

堆的插入

堆的实现原理是数组，所以我们使用尾插非常方便。但是堆的要求是父亲节点必须大于或小于孩子节点，所以我们在插入时有很多情况。就以小堆为例：

这里最坏的情况就是插入一个数，最后与根交换才能成为小堆。这里我们可以创建一个向上调整函数，当插入一个数据时，我们得进行比较调换让其继续保存小堆！！！

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

我们传入这个数组，再将新插入的数据下标给予向上调整函数，利用二叉树在数组中存储的规律找到父节点进行比较，如果子节点小于父节点则break退出循环，反之子节点大于父节点进行交换继续寻找交换后的父节点进行比较，直到满足小堆或child>0结束循环。

Swap交换函数： 

void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

而创建插入函数就与顺序表极为相似，先判断空间是否足够，然后将新的数据插入数组中，最后调用向上调整判断是否满足小堆条件。

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->capacity == php->size)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size - 1);
}

堆的删除

堆的删除中，我们删除数组的尾元素就没有意义，所以一般删除堆是删除堆顶元素。那怎么删除才能保证满足小堆条件呢？

我们不能直接将堆顶元素删除，然后将数组中的其他元素往前挪一位，这样有极大的可能不满足堆的条件。如果按照上述方法继续进行，然后从新使用向上调整进行排序这样时间复杂度会很高，那有什么方法可以优化呢？

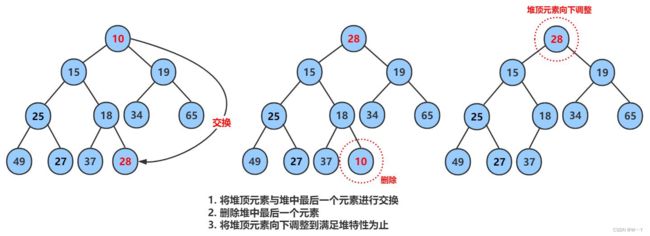
我们可以将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调
整算法。

将堆顶的元素交换到下面去先进行尾删覆盖，再进行向下调整就可以完成堆顶的删除。

那如何创建向下调整函数呢？

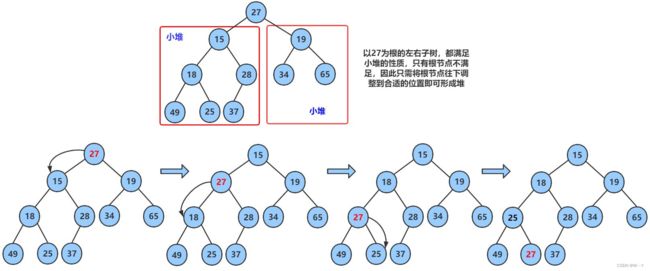
我们先创建将数组指针进行接收，然后传入数组的大小以及已经交换过需要调整元素的下标0

然后通过二叉树在数组中存储的规律找到左孩子节点，让左孩子与右孩子进行比较，谁小谁才有机会与父节点进行比较交换。以此类推即可满足小堆要求。

void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

特别注意：我们在找到左孩子节点之后，要让左孩子与右孩子进行比较时，我们必须要加入限制条件child+1

而删除堆函数就非常简单了，只需要将头与尾进行交换后调用向下调整函数即可。

void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);
	--php->size;

	AdjustDown(php->a, php->size, 0);
}

 堆实现的代码接口，以及简单函数的直接实现

typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}
// 堆的判空
int HeapEmpty(Heap* hp);
{
    assert(hp);
	return hp->size == 0;
}

---

以上就是二叉树的顺序结构以及堆排序实现的全部内容，下一篇文章我们就要学习关于堆最经典的堆排序以及topk问题，敬请期待。

感谢大家观看，一键三连是对博主最大的鼓励，博主因为你们的阅读而开心，希望博主的分享可以帮助许多人❤️❤️❤️