FIR滤波器简述及FPGA仿真验证
数字滤波器的设计,本项目做的数字滤波器准确来说是FIR滤波器。
FIR滤波器(有限冲激响应滤波器),与另一种基本类型的数字滤波器——IIR滤波器(无限冲击响应滤波器)相对应,其实就是将所输入的信号都看成是离散的,用离散的冲击信号代替实际的信号。对于FIR滤波器而言,就是将有限个最近输入的冲击信号进行加权平均运算得到新的输出信号,用以滤除其他不需要的信号。而IIR滤波器不仅需要对输入信号进行加权平均,对输出信号也要进行加权平均,从而得到新的输出信号,滤除其他不需要的信号。
FIR滤波器的算法就是类似卷积的算法。核心其实就是加权平均,即:
Y(n)=h(0)*x(n)+h(1)*x(n-1)+h(2)*x(n-2)+h(3)*x(n-3)+……+ h(N-1)*x(n-N+1)
X(n)是我们待滤波的信号,h(n)是滤波器系数。
在用Verilog编程之前用MATLAB计算出h(k)(k=0~N-1)权重。
对于FPGA而言,有两种方法可以实现FIR滤波器的设计,一种是通过Verilog语言编写,另一种是通过IP核实现。
用Verilog语言编写需要通过Matlab的工具箱生成h(k)(k=0~N-1)权重。而用IP核的话直接在软件里生成就行,本文是以Quartus软件为例。
本文刚开始还不想用IP核来生成的,并介绍了使用Matlab中FDATOOL工具箱的方法,然后后面改用了IP核的方式来完成FIR滤波器的设计与仿真。
Fdatool生成FIR相关的系数
打开matlab的fdatool工具箱。
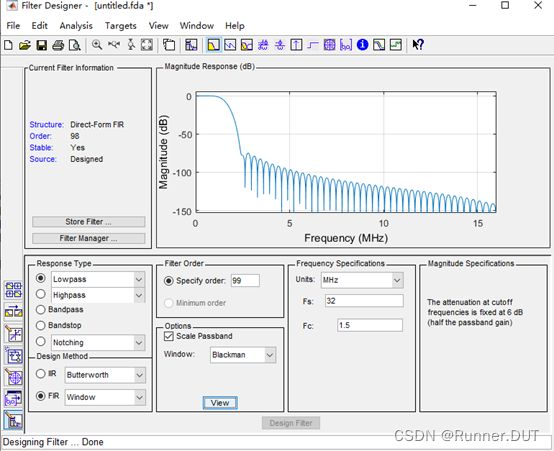
然后选择设计需要的滤波器,低通,FIR滤波器,窗函数设计(Window),采用布莱克曼窗(Blackman),99阶(这样有100个系数),采样频率50MHz,通带频率1.5MHz。
按照上图设定参数后,在上图中Specify order是阶数,Fc是截止频率,Fs是序列的采样频率。点击Design Filter。
设计完成了,可以看到显示的频率为0~Fs/2的幅频响应,大概在2MHz左右幅度下降为原来的-60dB以下,也就是正常幅度的千分之一。
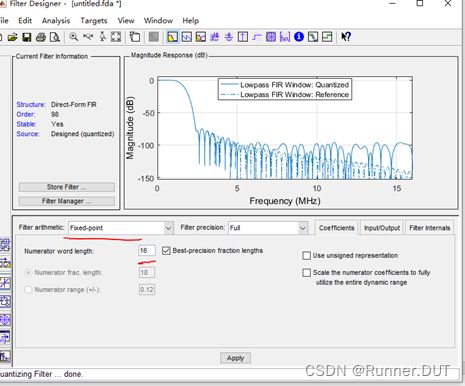
由于在FPGA中计算浮点数是一件很麻烦的事情,此处就设置成定点数,且位数越高越精确,这里设置的是16位定点数来量化。
然后点击Apply。下方图片中实线是量化后的,虚线是未量化过的精准的。可以看到虽然5MHz之后的阻带衰减不如原来,但也可以衰减到-100dB,也就是原来的1/100000。这个衰减程度已经足够了。
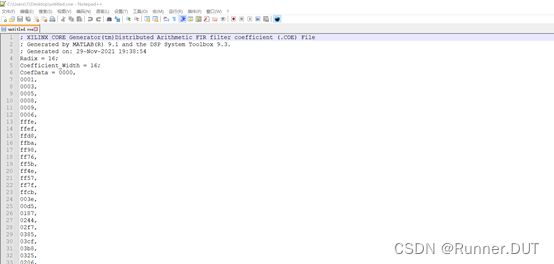
最后是导出系数。直接通过file——export导出的是没有经过量化的系数,通过量化的系数要经过Targets———XILINX Coefficient file导出.coe文件就可以查看量化后的数了。
新建Quartus工程设计FIR滤波器
首先创建好工程,这里不再赘述。
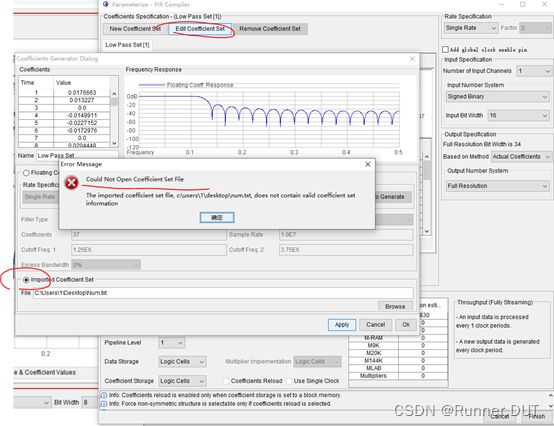
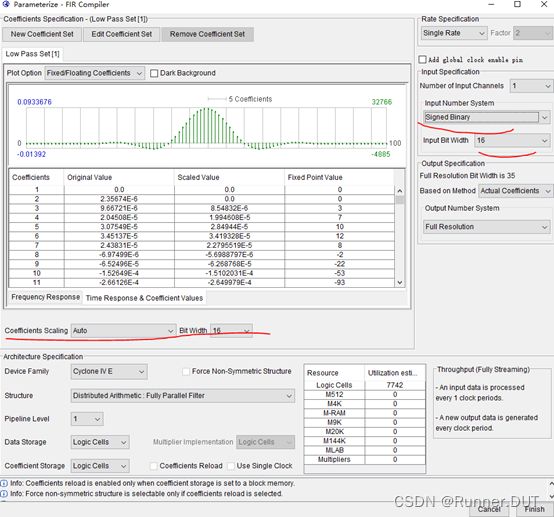
然后,生成FIR Compiler II 的IP核,随意先生成了一个,但是好像还不太对。后来才知道,应该选用FIR Complier v13.1的FIR IP核。首先进入step1,最开始要设置好滤波器系数,但是不知道为什么就是导不进去。如果可以导进去的话那么matlab中的fdatool工具箱我们就是用到了,但是问题就是导不进去。不过好在点击上面那个floating Coefficient Set可以自动生成浮点数的滤波器系数。
于是我们简单设置以下,让IP核自动生成相应的系数。
然后设置一下数据位宽
Step2的内容就全部勾选即可,然后进入step3自动生成IP核。
仿真
采用IP核的方式产生的FIR滤波器仿真的话直接通过编辑textbench仿真文件的方式仿真;采用Verilog语言编写方式产生的FIR滤波器在编辑textbench仿真文件之前还需对顶层.v文件进行编辑。
首先介绍采用IP核的方式仿真,一开始遇到的问题是关于FIR Compliter的IP核没有破解,后来需要改一下Licence文件才能使用。如下图所示,原来红框中是00A2,后来改成FIR Compliter的IP核的ID号,然后重启就能正常编译使用了。
然后遇到的问题是待滤波的数据和滤波后的数据分别是怎样输入进去以及怎样输出保存起来的。先做一种尝试,待滤波的数据通过Matlab生成并存放在.txt文档中,然后在仿真文件里调用该文档的数据,不过要注意采样周期和采样数据点的问题,也就是时序的问题。输出的数据的话先不用管,直接通过仿真看滤波后输出数据的变化即可。
编写Matlab程序产生待滤波信号,产生两个信号0.5MHz和5MHz,采样频率50MHz,采样5个周期,进行16-bit量化,并把量化后的数据写到.txt文件中。目前的问题在于怎么转换成16位二进制数。最后还是选择一种比较好的方法。首先判断读取的一个数是否大于零,如果大于零,直接采用dec2bin函数转换成16位的二进制数;如果小于零,则用216![]() 减去该数的绝对值,再用dec2bin函数将其转换成16位的二进制数。主要卡在如何分别读取每一个数上面,还是对matlab的操作不太熟悉。不过好在最后还是弄出来了。Matlab相关程序如下图所示。
减去该数的绝对值,再用dec2bin函数将其转换成16位的二进制数。主要卡在如何分别读取每一个数上面,还是对matlab的操作不太熟悉。不过好在最后还是弄出来了。Matlab相关程序如下图所示。
最终生成的十进制数和二进制数的txt文件内容如下图所示。
然后再学习一下FFT算法,利用matlab先对输入的数据进行频谱分析。有两种方法,一种是编写程序的方法,在MATLAB中,FFT的调用函数主要有两个,即:Y=FFT(X)和Y=FFT(X,N)。网上的例子:
clf;
fs=100;N=128; %采样频率和数据点数
n=0:N-1;t=n/fs; %时间序列
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号
y=fft(x,N); %对信号进行快速Fourier变换
mag=abs(y); %求得Fourier变换后的振幅
f=n*fs/N; %频率序列
subplot(2,2,1),plot(f,mag); %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('N=128');grid on;
一种是利用Simulink仿真模型的方法。首先导入数据,然后进入Simulink。利用Powergui模块进行FFT分析,加上一个Form warkspace和一个示波器就可以了,具体就不介绍。
我们只需要知道FFT输入的是按时间来划分的采样点数据,经过FFT运算之后得出的是按频率来划分的同样数据长度的数据。
之后我们进入最关键的阶段,即仿真阶段。我们只需要导入Matlab生成的待滤波信号,然后在仿真软件中观察滤波后的信号即可。
我们先编写好仿真文件。
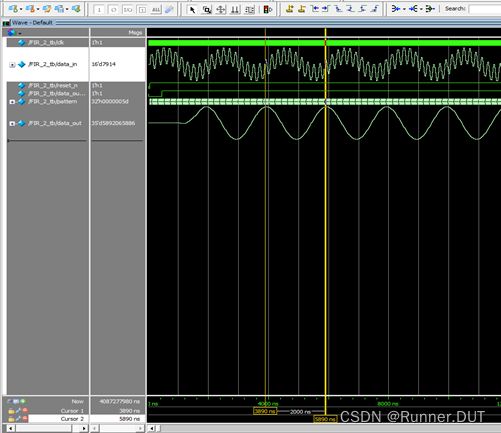
然后联合Modelsim仿真。右键data_in和data_out设置radix为decimal十进制,format为analog。
得到仿真结果,可以看到其周期为2000ns,即0.5MHz,表示5MHz干扰滤除干净了。
本文大部分内容都属于原创,如需转载,请附上本文网站,
如果需要相关的仿真图、程序代码等资料可以直接私信我,我会及时回复。