【数据结构】栈、队列和数组
栈、队列和数组
- 栈
- 队列
- 数组
-
- 数组的顺序表示和实现
-
- 顺序表中查找和修改数组元素
- 矩阵的压缩存储
-
- 特殊矩阵
- 稀疏矩阵
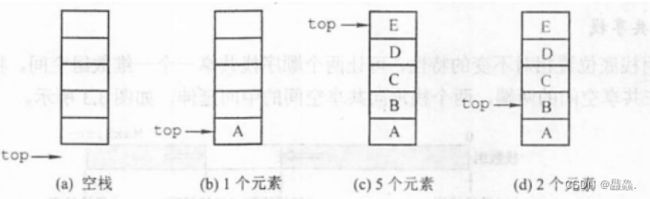
栈
#define MaxSize 50//栈中元素的最大个数
typedef char ElemType;
//数据结构
typedef struct{
int top;//栈顶指针
ElemType data[MaxSize];//存放栈中的元素
}SqStack;
//初始化栈,给top赋值为-1
void InitStack(SqStack *stack){
stack->top = -1;
}
判断是否为空
//判断栈是否为空,空返回true,反之即返回false
bool StackEmpty(SqStack stack){
if(stack.top==-1) return true;
return false;
}
进栈
//进栈
bool Push(SqStack *stack,ElemType e){
//判断是否满栈
if(stack->top==MaxSize-1) return false;
//指针先加1,再入栈
stack->data[++stack->top]=e;
return true;
}
出栈
//出栈
ElemType Pop(SqStack *stack){
//判断是否为空栈
if(stack->top==-1) return false;
//先取值,再自减
return stack->data[stack->top--];
}
读取栈顶元素
//读取栈顶元素
ElemType GetTop(SqStack stack){
//判断是否为空栈
if(stack.top==-1) return false;
return stack.data[stack.top];
}
队列
初始化
#define MaxSize 5
typedef char ElemType;
typedef struct
{
ElemType data[MaxSize];
int rear,front;
}SqQueue;
//初始化
void InitQueue(SqQueue *queue){
queue->front = queue->rear=0;
}
判断空
//判断是否为空,即判断首尾指针是否相等
bool QueueEmpty(SqQueue queue){
if(queue.front==queue.rear) return true;
return false;
}
入队
//入队
bool EnQueue(SqQueue *queue,ElemType e){
//判断是否是满队,即尾指针的下一个指向首指针
if((queue->rear+1)%MaxSize==queue->front) return false;
queue->data[queue->rear]=e;//赋值
//尾指针+1取模
queue->rear = (queue->rear+1)%MaxSize;
return true;
}
出队
//出队
ElemType DeQueue(SqQueue *queue){
//判断是否为空
if(queue->front==queue->rear) return false;
//先取值,首指针再+1取模
ElemType e = queue->data[queue->front];
queue->front++;
return e;
}
数组
提到数组,大家首先会想到的是:很多编程语言中都提供有数组这种数据类型,比如 C/C++、Java、Go、C# 等。但本节我要讲解的不是作为数据类型的数组,而是数据结构中提供的一种叫数组的存储结构。
和线性存储结构相比,数组最大的不同是:它存储的数据可以包含多种“一对一”的逻辑关系。举个简单的例子:
![]()
上图中,{a1, a2, a3, a4}、{b1, b2, b3, b4}、{c1, c2, c3, c4}、{d1, d2, d3, d4} 中各自包含的元素具有“一对一”的逻辑关系,同时 a、b、c、d 这 4 个序列也具有“一对一”的逻辑关系。
这样存储不止一种“一对一”逻辑关系的数据,数据结构就推荐使用数组存储结构。
对于数组存储结构,我们可以这样理解它:数组是对线性表的扩展,是一种“特殊”的线性存储结构,用来存储具有多种“一对一”逻辑关系的数据。
实际场景中,存储具有 N 种“一对一”逻辑关系的数据,通常会建立 N 维数组:
- 一维数组和其它线性存储结构很类似,用来存储只有一种“一对一”逻辑关系的数据:
![]()
- 二维数组用来存储包含两种“一对一”逻辑关系的数据。二维数组可以看作是存储一维数组的一维数组

- n 维数组用来存储包含 n 种“一对一”逻辑关系的数据,可以看作是存储 n-1 维数组的一维数组;
数组存储结构还具有一些其它的特性,包括:
- 无论数组的维度是多少,数组中的数据类型都必须一致;
- 数组一旦建立,它的维度将不再改变;
- 数组存储结构不会对内部的元素做插入和删除操作,常见的操作有 4 种,分别是初始化数组、销毁数组、取数组中的元素和修改数组中的元素。
数组的顺序表示和实现
数组可以是多维的,而顺序表只能是一维的线性空间。要想将 N 维的数组存储到顺序表中,可以采用以下两种方案:
- 以列序为主(先列后行):按照行号从小到大的顺序,依次存储每一列的元素;
- 以行序为主(先行后序):按照列号从小到大的顺序,依次存储每一行的元素。
多维数组中,最常用的是二维数组,接下里就以二维数组为例,讲解数组的顺序存储结构。
![]()
所示的二维数组按照“列序为主”的方案存储时,数组中的元素在顺序表中的存储状态如下图所示:
![]()
同样的道理,按照“行序为主”的方案存储数组时,各个元素在顺序表中的存储状态如图
![]()
顺序表中查找和修改数组元素
注意,只有在顺序表内查找到数组中的目标元素之后,才能对该元素执行读取和修改操作。
在 N 维数组中查找目标元素,需知道以下信息:
- 数组的存储方式;
- 数组在内存中存放的起始地址;
- 目标元素在数组中的坐标。比如说,二维数组中是通过行标和列标来确定元素位置的;
- 数组中元素的类型,即数组中单个数据元素所占内存的大小,通常用字母 L 表示;
根据存储方式的不同,查找目标元素的方式也不同。仍以二维数组为例,如果数组采用“行序为主”的存储方式,则在二维数组 anm 中查找 aij 位置的公式为:
LOC(i, j) = LOC(0, 0) + (i * m + j) * L;
其中,LOC(i, j) 为 aij 在内存中的地址,LOC(0, 0) 为二维数组在内存中存放的起始位置(也就是 a00 的位置)。
而如果采用以列存储的方式,在 anm 中查找 aij 的方式为:
LOC(i, j) = LOC(0, 0) + (j * n + i) * L;
根据以上两个公式,就可以在顺序表中找到目标元素,自然也就可以进行读取和修改操作了。
代码实现
#include矩阵的压缩存储
特殊矩阵
这里所说的特殊矩阵,主要分为以下两类:
- 含有大量相同数据元素的矩阵,比如对称矩阵;
- 含有大量 0 元素的矩阵,比如稀疏矩阵、上(下)三角矩阵;
针对以上两类矩阵,数据结构的压缩存储思想是:矩阵中的相同数据元素(包括元素 0)只存储一个
![]()
数据元素沿主对角线对应相等,这类矩阵称为对称矩阵,矩阵中有两条对角线,对角线称为主对角线,另一条从左下角到右上角的对角线为副对角线。对称矩阵指的是各数据元素沿主对角线对称的矩阵。
对称矩阵的实现过程是,若存储下三角中的元素,只需将各元素所在的行标 i 和列标 j 代入下面的公式:
![]()
存储上三角的元素要将各元素的行标 i 和列标 j 代入另一个公式:
![]()
最终求得的 k 值即为该元素存储到数组中的位置(矩阵中元素的行标和列标都从 1 开始)。
例如,在数组 skr[6] 中存储图 1 中的对称矩阵,则矩阵的压缩存储状态如图所示(存储上三角和下三角的结果相同):
![]()
注意,以上两个公式既是用来存储矩阵中元素的,也用来从数组中提取矩阵相应位置的元素。例如,如果想从图中的数组提取矩阵中位于 (3,1) 处的元素,由于该元素位于下三角,需用下三角公式获取元素在数组中的位置,即:
![]()
稀疏矩阵
![]()
如果矩阵中分布有大量的元素 0,即非 0 元素非常少,这类矩阵称为稀疏矩阵。
压缩存储稀疏矩阵的方法是:只存储矩阵中的非 0 元素,与前面的存储方法不同,稀疏矩阵非 0 元素的存储需同时存储该元素所在矩阵中的行标和列标。
例如,存储上图中的稀疏矩阵,需存储以下信息:
- (1,1,1):数据元素为 1,在矩阵中的位置为 (1,1);
- (3,3,1):数据元素为 3,在矩阵中的位置为 (3,1);
- (5,2,3):数据元素为 5,在矩阵中的位置为 (2,3);
- 除此之外,还要存储矩阵的行数 3 和列数 3;
![]()
**若对其进行压缩存储,矩阵中各非 0 元素的存储状态如图 **
![]()
三元组的结构体
//三元组结构体
typedef struct {
int i,j;//行标i,列标j
int data;//元素值
}triple;
由于稀疏矩阵中非 0 元素有多个,因此需要建立 triple 数组存储各个元素的三元组。除此之外,考虑到还要存储矩阵的总行数和总列数,因此可以采用以下结构表示整个稀疏矩阵:
#define number 20
//矩阵的结构表示
typedef struct {
triple data[number];//存储该矩阵中所有非0元素的三元组
int mu, nu, tu;//mu和nu分别记录矩阵的行数和列数,tu记录矩阵中所有的非0元素的个数
}TSMatrix;
#include