文章目录
- 一、python矩阵操作
- 二、python 矩阵乘法
- 三、python 矩阵转置
- 四、python 求方阵的迹
- 五、python 方阵的行列式计算方法
- 六、python 求逆矩阵 / 伴随矩阵
- 七、python 解多元一次方程
一、python矩阵操作
- 引入numpy, 使用mat函数创建一个2X3矩阵
import numpy as np
a=np.mat([[1,2,3],[4,5,6]])
a

- 使用 shape 可以获取矩阵的大小
a.shape

- 使用下表读取矩阵中的元素
a.T

- 进行行列转换
a.transpose()
a.T

- 使用二维数组代替矩阵来进行矩阵运算
b=np.array([[1,2,3],[4,5,6]])
b
b.T

- 加减法
a+a
b+b

- 列表是不能这么尽兴加减
c=[[1,2,3],[4,5,6]]
c+c

二、python 矩阵乘法
- 使用二维数组创建两个矩阵 A 和 B
A=np.array([[1,2,3],[4,5,6]])
B=A.T
A
B
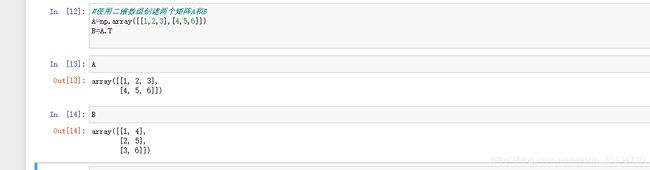
- 矩阵每个元素乘以该数
2*A
2*B

- dot 函数用于矩阵乘法,对于二维数组,它计算的是矩阵乘积,对于一维数组,它计算的是内积
A*B
np.dot(A,B)
np.dot(B,A)

- 创建一个二维数组
C=np.array([[1,2],[1,3]])
C

- 验证一个矩阵乘法的结合性:(AB)C=A(BC)
np.dot(np.dot(A,B),C)
np.dot(A,np.dot(B,C))

- 加法的分配性:(A+B)C=AC+BC、C(A+B)=CA+CB
D=B-1
D
np.dot(A,B+D)
np.dot(A,B)+np.dot(A,D)

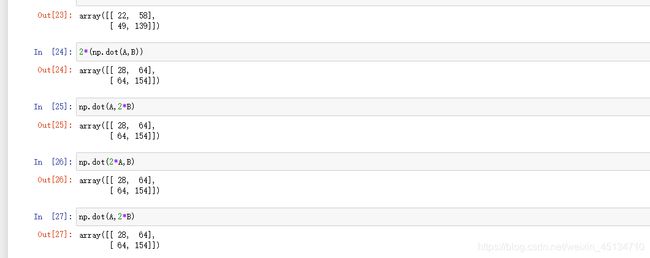
- 数乘的结合性
2*(np.dot(A,B))
np.dot(A,2*B)
np.dot(2*A,B)
np.dot(A,2*B)
- 使用 eye 创建一个单位矩阵
I=np.eye(3)
I

- 矩阵 A 乘以一个单位矩阵
np.dot(A,I)

三、python 矩阵转置
- 使用属性 T 来得到矩阵 A 的转置矩阵
A.T

- 验证:(A’)’=A
A.T.T

- 验证(A±B)’=A’±B’
(B+D).T
B.T+D.T

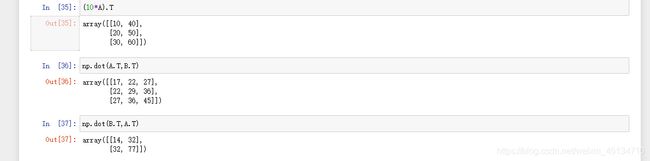
- 验证(KA)’=KA’
10*A.T
(10*A).T

- 验证(A×B)’=B’×A’
np.dot(A.T,B.T)
np.dot(B.T,A.T)
四、python 求方阵的迹
- 创建一个方阵(行数等于列数的矩阵)
E=np.array([[1,2,3],[4,5,6],[7,8,9]])
E

- trace 计算方阵的迹
np.trace(E)

- 创建一个方阵 F
F=E-2
F

- 验证一下方阵的迹等于方阵的转置的迹
np.trace(E)
np.trace(E.T)

- 验证一下方阵的乘积的迹
np.trace(np.dot(E,F))
np.trace(np.dot(F,E))

- 验证一下方阵的和的迹等于方阵的迹的和
np.trace(E+F)
np.trace(E)+np.trace(F)

五、python 方阵的行列式计算方法
- det 方法求得方阵 E 和方阵 F 的行列式
np.linalg.det(E)
np.linalg.det(F)

- 求得方阵 C
C
np.linalg.det(C)

六、python 求逆矩阵 / 伴随矩阵
- 创建一个方阵
A=np.array([[1,-2,1],[0,2,-1],[1,1,-2]])
A

- 使用 linalg.det 求得方阵的行列式
A_abs=np.linalg.det(A)
A_abs

- 使用 linalg.inv 求得方阵 A 的逆矩阵
B=np.linalg.inv(A)
B

- 公式法计算
A_bansui=B*A_abs
A_bansui

七、python 解多元一次方程
- 将未知数的系数写下来,排列成一个矩阵 a
a=[[1,2,1],[2,-1,3],[3,1,2]]
a=np.array(a)
a

- 常数项构成一个一维数组
b=[7,7,18]
b=np.array(b)
b

- 使用linalg.solve 方法解方程
x=np.linalg.solve(a,b)
x

- 使用点乘的方法可以验证一下
np.dot(a,x)




































