AcWing算法基础课第二讲(1):单链表、双链表、栈、队列、单调栈、单调队列、KMP

1. 单链表

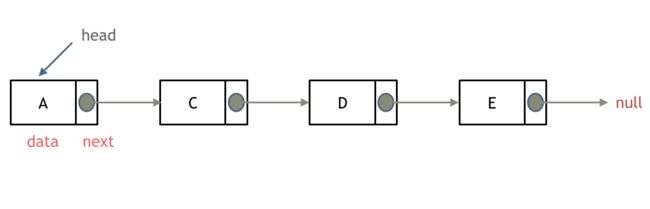
• 什么是链表，链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。

• 单链表可用来创建邻接表，邻接表主要用于存储树和图。

• 链表的入口节点称为链表的头结点也就是head。
  
  接下来我将介绍的是用数组来模拟单链表，通过数组来实现单链表的功能。

• 创建两个数组e[N]、ne[N]，其中：e[N]存放节点的值，ne[N]存放指向下一个节点的指针，最后一个节点的指针域指向-1（用-1表示链表末尾的空指针），如图所示：
  

• 链表初始化、插入节点以及删除节点，如图所示：
  

单链表模版

• head存储链表头，e[]存储节点的值，ne[]存储节点的next指针，idx表示当前用到了哪个节点

int head, e[N], ne[N], idx;

• 链表初始化
  

void init()
{
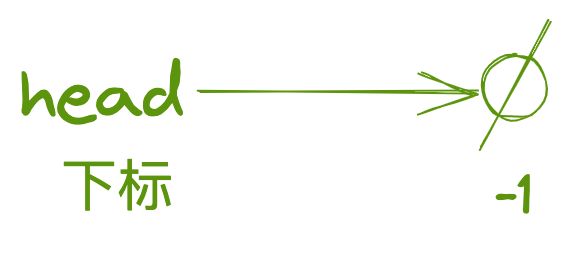
    head = -1;
    idx = 0;
}

• 在链表头插入一个数x
  

void insert(int x)
{
    e[idx] = x, ne[idx] = head, head = idx ++ ;
}

• 将x插入下标是k的点后面
  

void insert(int k, int x)
{
    e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++ ;
}

• 将头结点删除，需要保证头结点存在
  

void remove()
{
    head = ne[head];
}

• 将下标是k的点后面的点删除
  

void remove(int k)
{
    ne[k] = ne[ne[k]];
}

模板题 AcWing 826. 单链表
实现一个单链表，链表初始为空，支持三种操作：

1. 向链表头插入一个数；
2. 删除第 k 个插入的数后面的数；
3. 在第 k 个插入的数后插入一个数。

现在要对该链表进行 M 次操作，进行完所有操作后，从头到尾输出整个链表。

注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式
第一行包含整数 M，表示操作次数。
接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：

1. H x，表示向链表头插入一个数 x。
2. D k，表示删除第 k 个插入的数后面的数（当 k 为 0 时，表示删除头结点）。
3. I k x，表示在第 k 个插入的数后面插入一个数 x（此操作中 k 均大于 0）。

输出格式
共一行，将整个链表从头到尾输出。

数据范围
1≤M≤100000
所有操作保证合法。

输入样例：
10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6

输出样例：
6 4 6 5

#include 

using namespace std;

const int N = 100010;


// head 表示头结点的下标
// e[i] 表示节点i的值
// ne[i] 表示节点i的next指针是多少
// idx 存储当前已经用到了哪个点
int head, e[N], ne[N], idx;

// 初始化
void init()
{
    head = -1;
    idx = 0;
}

// 将x插到头结点
void add_to_head(int x)
{
    e[idx] = x, ne[idx] = head, head = idx ++ ;
}

// 将x插到下标是k的点后面
void add(int k, int x)
{
    e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++ ;
}

// 将下标是k的点后面的点删掉
void remove(int k)
{
    ne[k] = ne[ne[k]];
}

int main()
{
    int m;
    cin >> m;

    init();

    while (m -- )
    {
        int k, x;
        char op;

        cin >> op;
        if (op == 'H')
        {
            cin >> x;
            add_to_head(x);
        }
        else if (op == 'D')
        {
            cin >> k;
            if (!k) head = ne[head];
            else remove(k - 1);
        }
        else
        {
            cin >> k >> x;
            add(k - 1, x);
        }
    }

    for (int i = head; i != -1; i = ne[i]) cout << e[i] << ' ';
    cout << endl;

    return 0;
}

2. 双链表

• 单链表中的指针域只能指向节点的下一个节点。
  双链表：每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点。
  双链表 既可以向前查询也可以向后查询。
  如图所示：
  
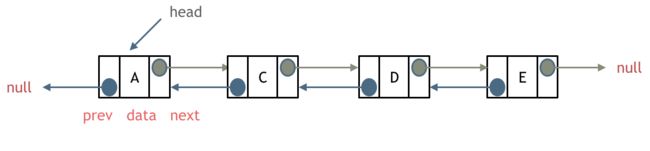
  接下来我将介绍用数组来模拟双链表，通过数组来实现双链表的功能。
• 创建三个数组e[N]、l[N]、r[N]，其中：e[N]表示节点的值，l[N]表示节点的左指针，r[N]表示节点的右指针；
• idx表示当前用到了哪个节点；
• 初始化双链表时，用0表示左端点head，1表示右端点tail

双链表模版

• e[N]表示节点的值，l[N]表示节点的左指针，r[N]表示节点的右指针，idx表示当前用到了哪个节点

int e[N], l[N], r[N], idx;

• 链表初始化
  

void init()
{
    //0是左端点，1是右端点
    r[0] = 1, l[1] = 0;
    idx = 2; //由于0和1分别表示左右端点，因此idx初始化为2
}

• 在下标是k的点的右边，插入x
  

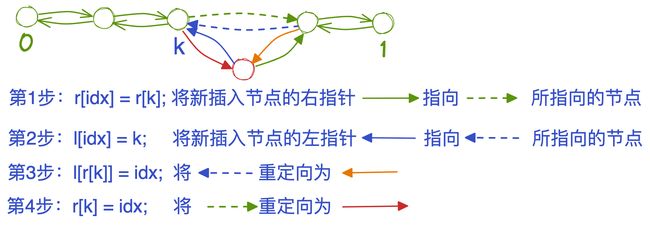
void add(int k, int x)
{
    e[idx] = x;
    r[idx] = r[k], l[idx] = k;
    l[r[k]] = idx, r[k] = idx ++;
}

• 删除下标为k的节点
  

void remove(int k)
{
    l[r[k]] = l[k];
    r[l[k]] = r[k];
}

模板题 AcWing 827. 双链表
实现一个双链表，双链表初始为空，支持 5 种操作：

1. 在最左侧插入一个数；
2. 在最右侧插入一个数；
3. 将第 k 个插入的数删除；
4. 在第 k 个插入的数左侧插入一个数；
5. 在第 k 个插入的数右侧插入一个数

现在要对该链表进行 M 次操作，进行完所有操作后，从左到右输出整个链表。

注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式
第一行包含整数 M，表示操作次数。
接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：

1. L x，表示在链表的最左端插入数 x。
2. R x，表示在链表的最右端插入数 x。
3. D k，表示将第 k 个插入的数删除。
4. IL k x，表示在第 k 个插入的数左侧插入一个数。
5. IR k x，表示在第 k 个插入的数右侧插入一个数。

输出格式
共一行，将整个链表从左到右输出。

数据范围
1≤M≤100000
所有操作保证合法。

输入样例：
10
R 7
D 1
L 3
IL 2 10
D 3
IL 2 7
L 8
R 9
IL 4 7
IR 2 2

输出样例：
8 7 7 3 2 9

#include 

using namespace std;

const int N = 100010;

int m;
int e[N], l[N], r[N], idx;

// 在节点a的右边插入一个数x
void insert(int a, int x)
{
    e[idx] = x;
    l[idx] = a, r[idx] = r[a];
    l[r[a]] = idx, r[a] = idx ++ ;
}

// 删除节点a
void remove(int a)
{
    l[r[a]] = l[a];
    r[l[a]] = r[a];
}

int main()
{
    cin >> m;

    // 0是左端点，1是右端点
    r[0] = 1, l[1] = 0;
    idx = 2;

    while (m -- )
    {
        string op;
        cin >> op;
        int k, x;
        if (op == "L")
        {
            cin >> x;
            insert(0, x);
        }
        else if (op == "R")
        {
            cin >> x;
            insert(l[1], x);
        }
        else if (op == "D")
        {
            cin >> k;
            remove(k + 1);
        }
        else if (op == "IL")
        {
            cin >> k >> x;
            insert(l[k + 1], x);
        }
        else
        {
            cin >> k >> x;
            insert(k + 1, x);
        }
    }

    for (int i = r[0]; i != 1; i = r[i]) cout << e[i] << ' ';
    cout << endl;

    return 0;
}

3. 栈

• 栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。栈具有“先进后出”的特性。
  
  接下来我将介绍的是用数组来模拟栈，通过数组来实现栈的功能。

栈的模版

tt表示栈顶
int stk[N], tt = 0;

向栈顶插入一个数
stk[ ++ tt] = x;

从栈顶弹出一个数
tt -- ;

栈顶的值
stk[tt];

判断栈是否为空

if (tt > 0) not empty
else empty

模板题 AcWing 828. 模拟栈
实现一个栈，栈初始为空，支持四种操作：

1. push x – 向栈顶插入一个数 x；
2. pop – 从栈顶弹出一个数；
3. empty – 判断栈是否为空；
4. query – 查询栈顶元素。

现在要对栈进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式
第一行包含整数 M，表示操作次数。
接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式
对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。
其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示栈顶元素的值。

数据范围
1≤M≤100000,
1≤x≤10⁹
所有操作保证合法。

输入样例：
10
push 5
query
push 6
pop
query
pop
empty
push 4
query
empty

输出样例：
5
5
YES
4
NO

#include 

using namespace std;

const int N = 100010;

int m;
int stk[N], tt;

int main()
{
    cin >> m;
    while (m -- )
    {
        string op;
        int x;

        cin >> op;
        if (op == "push")
        {
            cin >> x;
            stk[ ++ tt] = x;
        }
        else if (op == "pop") tt -- ;
        else if (op == "empty") cout << (tt ? "NO" : "YES") << endl;
        else cout << stk[tt] << endl;
    }

    return 0;
}

4. 队列

1）普通队列

• 队列（queue）是一种特殊的线性表，特殊之处在于它只允许在表的前端进行删除操作，而在表的后端进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列具有“先进先出”的特性。
  
  接下来我将介绍的是用数组来模拟队列，通过数组来实现队列的功能。

普通队列模版

hh 表示队头，tt表示队尾
int q[N], hh = 0, tt = -1;

向队尾插入一个数
q[ ++ tt] = x;

从队头弹出一个数
hh ++ ;

队头的值
q[hh];

判断队列是否为空

if (hh <= tt) not empty
else empty

模板题 AcWing 829. 模拟队列
实现一个队列，队列初始为空，支持四种操作：

1. push x – 向队尾插入一个数 x；
2. pop – 从队头弹出一个数；
3. empty – 判断队列是否为空；
4. query – 查询队头元素。

现在要对队列进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式
第一行包含整数 M，表示操作次数。
接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式
对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。
其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示对头元素的值。

数据范围
1≤M≤100000,
1≤x≤10⁹
所有操作保证合法。

输入样例：
10
push 6
empty
query
pop
empty
push 3
push 4
pop
query
push 6

输出样例：
NO
6
YES
4

#include 

using namespace std;

const int N = 100010;

int m;
int q[N], hh, tt = -1;

int main()
{
    cin >> m;

    while (m -- )
    {
        string op;
        int x;

        cin >> op;
        if (op == "push")
        {
            cin >> x;
            q[ ++ tt] = x;
        }
        else if (op == "pop") hh ++ ;
        else if (op == "empty") cout << (hh <= tt ? "NO" : "YES") << endl;
        else cout << q[hh] << endl;
    }

    return 0;
}

2）循环队列

循环队列模版

hh 表示队头，tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;

向队尾插入一个数

q[tt ++ ] = x;
if (tt == N) tt = 0;

从队头弹出一个数

hh ++ ;
if (hh == N) hh = 0;

队头的值
q[hh];

判断队列是否为空

if (hh != tt) not empty
else empty

5. 单调栈

• 常见模型：找出序列当中每个数左边离它最近的比它大/小的数。

暴力做法

for (int i = 0; i < n; i++)
	for (int j = i - 1; j >= 0; j--)
		if (a[i] > a[j]) {
			cout << a[j] << endl;
			break;
		}

单调栈模版

int tt = 0;
for (int i = 1; i <= n; i ++ )
{
    while (tt && check(stk[tt], i)) tt -- ;
    stk[ ++ tt] = i;
}

模板题 AcWing 830. 单调栈
给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

输入格式
第一行包含整数 N，表示数列长度。
第二行包含 N 个整数，表示整数数列。

输出格式
共一行，包含 N 个整数，其中第 i 个数表示第 i 个数的左边第一个比它小的数，如果不存在则输出 −1。

数据范围
1≤N≤10⁵
1≤数列中元素≤10⁹

输入样例：
5
3 4 2 7 5

输出样例：
-1 3 -1 2 2

#include 
using namespace std;

const int N = 1e5 + 10;
int stk[N], tt = 0;

int main() {
    int n;
    scanf("%d", &n);
    while (n--) {
        int x;
        scanf("%d", &x);
        while (tt && stk[tt] >= x) tt--; //当栈中存在元素并且栈顶元素大于x时，从栈中弹出栈顶元素
        if (tt == 0) printf("-1 "); //当未在栈中查找到小于x的元素时，栈中所有元素均被弹出，此时栈为空，输出-1
        else printf("%d ", stk[tt]); //当存在栈顶元素小于x时，将此栈顶元素输出
        stk[++tt] = x; //将x插入到栈顶
    }
    return 0;
}

6. 单调队列

• 常见模型：找出滑动窗口中的最大值/最小值

思路：
1）先思考如何使用普通队列来解题
2）将滑动队列中永远不会作为答案输出的元素删掉——>观察滑动窗口中的队列是否具有单调性
3）使用单调队列可以用O(1)的时间从队头/队尾取出最值

单调队列模版

int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
    while (hh <= tt && check_out(q[hh])) hh ++ ;  // 判断队头是否滑出窗口
    while (hh <= tt && check(q[tt], i)) tt -- ;
    q[ ++ tt] = i;
}

模板题 AcWing 154. 滑动窗口
给定一个大小为 n≤10⁶ 的数组。
有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。
你只能在窗口中看到 k 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子：
该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式
输入包含两行。
第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数，代表数组的具体数值。
同行数据之间用空格隔开。

输出格式
输出包含两个。
第一行输出，从左至右，每个位置滑动窗口中的最小值。
第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：
8 3
1 3 -1 -3 5 3 6 7

输出样例：
-1 -3 -3 -3 3 3
3 3 5 5 6 7

思路：
最小值和最大值分开来做，两个for循环完全类似，都做以下四步：

1. 解决队头已经弹出窗口的问题;
2. 解决队尾与当前元素a[i]不满足单调性的问题;
3. 将当前元素下标加入队尾;
4. 如果满足条件则输出结果;

需要注意的细节：

1. 上面四个步骤中一定要先3后4，因为有可能输出的正是新加入的那个元素;
2. 队列中存的是原数组的下标，取值时要再套一层，a[q[]];
3. 计算最大值前注意将hh和tt重置;
4. 此题用cout会超时，只能用printf;
5. hh从0开始，数组下标也要从0开始。

#include 

using namespace std;

const int N = 1000010;

int a[N], q[N];

int main()
{
    int n, k;
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);

    int hh = 0, tt = -1;
    for (int i = 0; i < n; i ++ )
    {
        if (hh <= tt && i - k + 1 > q[hh]) hh ++ ; // 若队首出窗口，hh加1
        while (hh <= tt && a[q[tt]] >= a[i]) tt -- ; // 若队列不单调，就将队尾弹出
        q[ ++ tt] = i; // 下标加到队尾
        if (i >= k - 1) printf("%d ", a[q[hh]]); // 输出结果
    }

    puts("");

    hh = 0, tt = -1; // 重置
    for (int i = 0; i < n; i ++ )
    {
        if (hh <= tt && i - k + 1 > q[hh]) hh ++ ;
        while (hh <= tt && a[q[tt]] <= a[i]) tt -- ;
        q[ ++ tt] = i;
        if (i >= k - 1) printf("%d ", a[q[hh]]);
    }

    puts("");

    return 0;
}

7. KMP

• 什么是KMP？
  KMP是由三位前辈D.E.Knuth、J.H.Morris和V.R.Pratt（其中Knuth和Pratt共同研究，Morris独立研究）发表的一个模式匹配算法，可以大大避免重复遍历的情况，我们把它称之为克努特-莫里斯-普拉特算法，简称KMP算法。

KMP模版
s[]是长文本，p[]是模式串，n是s的长度，m是p的长度

求模式串的next数组：
for (int i = 2, j = 0; i <= m; i ++ )
{
    while (j && p[i] != p[j + 1]) j = ne[j];
    if (p[i] == p[j + 1]) j ++ ;
    ne[i] = j;
}

匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
    while (j && s[i] != p[j + 1]) j = ne[j];
    if (s[i] == p[j + 1]) j ++ ;
    if (j == m)
    {
        j = ne[j];
        匹配成功后的逻辑
    }
}

模板题 AcWing 831. KMP字符串
给定一个字符串 S，以及一个模式串 P，所有字符串中只包含大小写英文字母以及阿拉伯数字。
模式串 P 在字符串 S 中多次作为子串出现。
求出模式串 P 在字符串 S 中所有出现的位置的起始下标。

输入格式
第一行输入整数 N，表示字符串 P 的长度。
第二行输入字符串 P。
第三行输入整数 M，表示字符串 S 的长度。
第四行输入字符串 S。

输出格式
共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。

数据范围
1≤N≤10⁵
1≤M≤10⁶

输入样例：
3
aba
5
ababa

输出样例：
0 2

题解：

一、解决该题需要了解的知识和相关概念：

1. s[ ]是文本串，即比较长的字符串。
2. p[ ]是模式串，即比较短的字符串。
3. “非平凡前缀”：指除了最后一个字符以外，一个字符串的全部头部组合。简称为前缀。
4. “非平凡后缀”：指除了第一个字符以外，一个字符串的全部尾部组合。简称为后缀。
5. 部分匹配值：前缀和后缀的最长共有元素的长度。
6. next[ ]是“部分匹配值表”，即next数组，它存储的是每一个下标对应的“部分匹配值”，是KMP算法的核心。

KMP主要分两步：

1. 求模式串的next[]数组
2. 匹配模式串

匹配模式串p[ ]和文本串s[ ]的核心思想：
在每次匹配不成功时，如s串的s[i - j] ~ s[i - 1]元素与p串的p[1]～p[j]元素匹配，而s[i] != p[j + 1]，那么就需要移动p串，然后重新在s串中匹配p串，这里不是将p串往后移一位，因为这会导致重复遍历，而是将p串往后移动至下一次可以和前面部分匹配的位置，这样就可以跳过大多数的失配步骤。而每次p串移动的步数就是通过查找next[ ]数组确定的。这样s串就可以继续从上一次匹配不成功的位置s[i]和p串移动后j的下一个位置p[j + 1]开始匹配。

二、next数组的含义及手动模拟

next数组的含义：对next[j] ，是p[1, j]串中前缀和后缀相同的最大长度（部分匹配值），即 p[1, next[j]]=p[j-next[j]+1, j]。
例如p串为“abaab”，那么next[5] = 2，如下图所示：

手动模拟求next数组：
p = “abcab”

• "a"的前缀和后缀都为空集，共有元素的长度为0；
• "ab"的前缀为[a]，后缀为[b]，共有元素的长度为0；
• "abc"的前缀为[a, ab]，后缀为[bc, c]，共有元素的长度0；
• "abca"的前缀为[a, ab, abc]，后缀为[bca, ca, a]，共有元素的长度为1；
• "abcab"的前缀为[a, ab, abc, abca]，后缀为[bcab, cab, ab, a]，共有元素为"ab"，长度为2；

三、匹配模式串的思路和实现代码

s串 和 p串都是从1开始的。i从1开始，j从0开始，因此每次s[i]和p[j + 1]进行比较

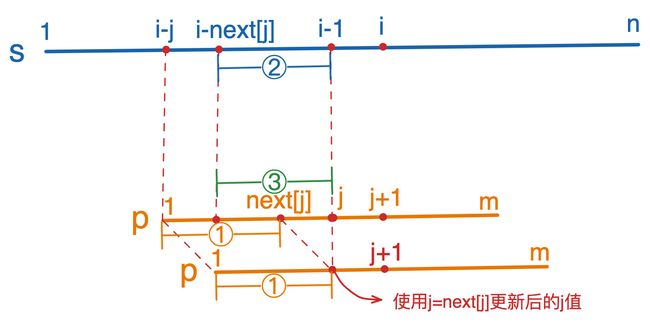
匹配过程到上图所示，
当s[i - j, i - 1 ] = p[1, j] && s[i] != p[j + 1]时，要移动p串，将p串移动到下次能直接从p[j + 1]和s[i]继续进行比较的位置。
其中①串为[1, next[j]]，③串为[j - next[j] + 1, j]。由匹配可知①串等于③串，③串等于②串。所以将p串从①移动到③的位置即可。这个操作可由j = next[j]直接完成。 如此往复下去，当s[i] = p[j + 1] && j + 1 = m时匹配成功。

代码如下：

for(int i = 1, j = 0; i <= n; i++)
{
    while(j && s[i] != p[j+1]) j = ne[j];
    //如果j有对应p串的元素， 且s[i] != p[j+1], 则失配，移动p串
    //用while是由于移动后可能仍然失配，所以要继续移动直到匹配或整个p串移到后面（j = 0)

    if(s[i] == p[j+1]) j++;
    //当前元素匹配，j移向p串下一位
    if(j == m)
    {
        //匹配成功，进行相关操作
        j = ne[j];  //继续匹配下一个子串
    }
}

四、求模式串的next数组的思路和实现代码

next数组的求法是通过模板串自己与自己进行匹配操作得出来的（代码和匹配操作几乎一样）。

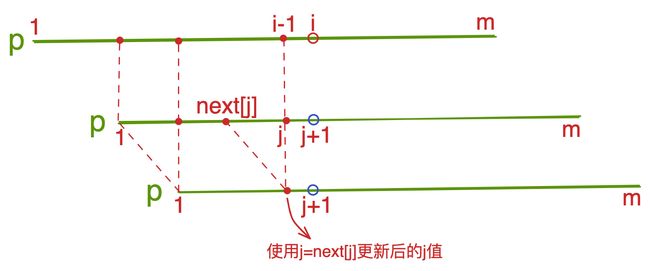
对于p串的字串p[1 ~ i]，由于已经通过循环遍历知道p串的字串p[1 ~ i-1]的最长公共前后缀长度，所以我们只需要判断p[i]是否与p[j + 1]相等，如果p[i] != p[j + 1] && j != 0，就需要将前缀进行回退，通过j = next[j]更新j值。

• 如果更新后的j = 0 && p[i] = p[j + 1]，则表明p串的字串p[1 ~ i]的最长公共前后缀分别是p[1]和p[i]，因此：将j++，next[i] = j也就相当于next[i] = 1；
• 如果更新后的j = 0 && p[i] != p[j + 1]，则表明p串的字串p[1 ~ i]没有最长公共前后缀，因此：next[i] = j也就相当于next[i] = 0；
• 如果更新后的j != 0 && p[i] = p[j + 1]，则表明p串的字串p[1 ~ i]的最长公共前缀分别是p[j + 1]，因此：将j++，这时next[i] = j；

求模式串的next数组的代码如下

for (int i = 2, j = 0; i <= m; i ++ ) //i从2开始遍历，因为当i = 1时，i的前后缀都为空，next[1] = 0
{
    while (j && p[i] != p[j + 1]) j = ne[j]; //通过回退j，更新j值
    if (p[i] == p[j + 1]) j ++ ; 
    ne[i] = j; //得到p串的第i个元素的next[i]值
}

五、完整代码

// 注：这不是题目的AC代码，是一个最基本的模板代码
#include 

using namespace std;

const int N = 1000010, M = 100010; //N为文本串长度，M为模式串长度

int n, m;
int ne[M]; //next[]数组，避免和头文件next冲突
char s[N], p[M];  //s为文本串， p为模式串

int main()
{
    cin >> m >> p + 1 >> n >> s+1;  //下标从1开始

    //求next[]数组
    for(int i = 2, j = 0; i <= m; i++) //i从2开始遍历，因为当i = 1时，i的前后缀都为空，next[1] = 0
    {
        while(j && p[i] != p[j+1]) j = ne[j]; //通过回退j，更新j值
        if(p[i] == p[j+1]) j++;
        ne[i] = j; //得到p串的第i个元素的next[i]值
    }
    //匹配模式串
    for(int i = 1, j = 0; i <= n; i++)
    {
        while(j && s[i] != p[j+1]) j = ne[j]; //通过回退j，更新j值
        if(s[i] == p[j+1]) j++;
        if(j == m)  //满足匹配条件，打印开头下标, 从0开始
        {
            //匹配成功后的具体操作
            //如：输出以0开始的匹配子串的首字母下标
            printf("%d ", i - m); (若从1开始，加1)
            j = ne[j];            //再次继续匹配
        }
    }

    return 0;
}

以上模版和笔记参考：
来源：AcWing 作者：yxc 链接：https://www.acwing.com/blog/content/277/
来源：AcWing 作者：四谷夕雨 链接：https://www.acwing.com/solution/content/14666/
来源：代码随想录 作者：孙秀洋 链接：https://www.programmercarl.com/0028.%E5%AE%9E%E7%8E%B0strStr.html
来源：阮一峰的个人网站 作者：阮一峰 链接：http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html