2022年全国研究生数学建模竞赛华为杯E题草原放牧策略研究求解全过程文档及程序

2022年全国研究生数学建模竞赛华为杯

E题 草原放牧策略研究

原题再现：

  一、背景介绍
  草原作为世界上分布最广的重要的陆地植被类型之一，分布面积广泛。中国的草原面积为3.55亿公顷，是世界草原总面积的6%~8%，居世界第二。此外，草原在维护生物多样性、涵养水土、净化空气、固碳、调节水土流失和沙尘暴等方面具有重要的生态功能。自2003 年党中央、国务院实施“退牧还草”政策以来，在保护和改善草原生态环境、改善民生方面取得了显著成效。“退牧还草”并不是禁止放牧，除了部分区域禁牧外，很多草原实行划区轮牧以及生长季休牧。合理的放牧政策是带动区域经济、防止草原沙漠化及保障民生的关键，放牧优化问题的研究也为国家、政府制定放牧政策和草原管理决策提供科学的依据。
  中国草原主要分为温带草原、高寒草原和荒漠草原等类型。内蒙古锡林郭勒草原是温带草原中具有代表性和典型性的草原，是中国四大草原之一，位于内蒙古高原锡林河流，地理坐标介于东经 110°50′至119°58′,北纬41°30′~46°45′之间，年均降水量340mm。内蒙古锡林郭勒草原不仅是国家重要的畜牧业生产基地，同时也是重要的绿色生态屏障，在减少沙尘暴和恶劣天气的发生方面发挥着作用，也是研究生态系统对人类干扰和全球气候变化响应机制的典型区域之一和国际地圈—生物圈计划（IGBP）陆地样带—中国东北陆地生态系统样带（NECT）的重要组成部分。
  关于草原放牧通常要考虑放牧方式和放牧强度（单位面积牲畜密度）2个因素。放牧方式可以分为多种，有文献将放牧方式分为以下五种，分别为：全年连续放牧、禁牧、选择划区轮牧、轻度放牧、生长季休牧。放牧强度可以分为四种，分别为：对照、轻度放牧强度、中度放牧强度、重度放牧强度。附件14、15中数据将选择划区轮牧的放牧强度分为：对照（NG， 0羊/天/公顷 ）、轻度放牧强度（LGI， 2羊/天/公顷 ）、中度放牧强度（MGI，4羊/天/公顷 ）和重度放牧强度（HGI，8羊/天/公顷 ）。实际中，也可以做如下的划分：对照（NG， 0羊/天/公顷 ）、轻度放牧强度（LGI， 1-2羊/天/公顷 ）、中度放牧强度（MGI，3 -4羊/天/公顷 ）和重度放牧强度（HGI，5-8羊天/公顷 ）。
  植物的生长满足自身的生长规律，同时受到周围环境的影响。例如，降水、温度、土壤湿度、土壤PH、营养等都决定植物的生长情况。当牧羊（家畜日食量为1.8kg，即标准羊单位，也包括羊羔。大牲畜折算系数6.0，比如牛、马、骆驼，大牲畜幼崽折算系数3.0 ）对植物进行采食时，一方面植物的地上生物量减少；另一方面，放牧对植物有刺激作用，改变了植物原有的生长速率，适当的放牧会刺激植物的超补偿生长，同样不合理的放牧也会降低植物的生长速率。
过度放牧，往往因牲畜密度过大，可能导致草原植被结构破坏，土壤裸露面积增大，促进了土壤表面的蒸发，土体内水分相对运动受到不利影响，破坏了土壤积盐与脱盐平衡，增加了盐分在土壤表面的积累，土壤盐碱化程度加重。最终造成草场退化、土地沙漠化。
  适度的放牧可以改善草原土壤质量、提高草原生物的多样性。一方面由于家畜的采食践踏造成枯落物分解，充分进入土壤，从而提高土壤有机质和氮和钾含量，减少土壤的板结。另一方面放牧能够降低表层土壤湿度、PH，一定程度增加土壤容重。土壤氮、磷、钾的含量及比例是土壤有机质组成和质量程度的重要指标。磷元素含量多少会影响土壤中凋落物的分解速率、微生物数量及活性以及有机碳和养分的积累。钾元素能够促进植物生理代谢，增强抗逆性，并促进植物对氮素营养的吸收和利用。土壤全氮含量随着放牧强度的增加而降低。有研究表明：高寒草甸的土壤全氮含量沿着放牧梯度呈下降趋势。因此，为了保证土壤达到合适的状态，找到放牧羊（标准羊）数量的阈值是问题的关键。
  土壤沙漠化又被称为沙质沙漠化，是荒漠化的一种主要表现类型。沙漠化是在干旱、半干旱和部分半湿润地区的沙物质基础和干旱大风动力条件下，由于自然因素或人为活动的影响，致使自然的生态系统平衡性遭到破坏，出现了以风沙活动为主要标志，并逐渐形成风蚀、风积地貌景观的环境退化过程，使原来没有沙漠景观的地区出现了类似沙漠景观的环境变化。所谓土壤板结化是指土壤打破了原有结构，表层的有机质遭到严重破坏而造成的，土壤板结原因很多，比如土壤贫瘠、容重过大、土壤质地太粘以及有机肥严重不足等。
  沙漠化程度指数（SM）是从数学的范畴去界定沙漠化程度，采用一定的分级标准使得其与沙漠化程度相对应。把沙漠化程度划分为五类：非沙漠化、轻度沙漠化、中度沙漠化、重度沙漠化和极重度沙漠化，SM 采用 0～1 标度法。

  土壤湿度越少，容重越大，有机物含量越低，土壤板结化程度越严重。
  土壤化学性质和物理性质是影响土壤肥力重要因素，土壤化学性质包括：土壤有机碳SOC、土壤无机碳SIC、土壤全碳STC、全N、土壤C/N比等；土壤物理性质包括：土壤湿度、土壤容重等。一般来说，在保持土壤化学性质等基本不变情况下，降水会增加土壤湿度，而土壤湿度增加会提高草场植被覆盖率，在良好的植被覆盖情况下可以适当提高放牧强度，在一定区域内，放牧强度越高意味着更多的放牧数量，在不考虑放牧补贴和价格波动情况下，更多放牧数量代表更高的放牧收益。
  现代草地资源的经营应遵循可持续发展原则，在保证生态环境良性健康发展中寻求经济利益的最大化。美国著名生态经济学家赫尔曼·E·戴利给可持续发展的定义是:“可持续发展是经济规模增长没有超越生物环境承载能力的发展”。 其理念是“可持续发展的整个理念就是经济子系统的增长规模绝对不能超越生态系统可以永远持续或支撑的容纳范围”。在草原区域系统中，承载力是评价可持续发展的一种工具。在《远东英汉大辞典》中，承载力被定义为“某一自然环境所能容纳的生物数目（指最高限度）”。区域生态系统承载力和可持续发展是相辅相成的两个概念。

  二、需解决问题：
  请你根据附件数据以及收集有关草原数据（土壤容重、土壤PH等），由于历史原因，数据虽然并不充分，实际问题仍然需要解决。请通过数学建模完成下列问题：
  问题1. 从机理分析的角度，建立不同放牧策略（放牧方式和放牧强度）对锡林郭勒草原土壤物理性质（主要是土壤湿度）和植被生物量影响的数学模型。
  问题2. 请根据附件3土壤湿度数据、附件4土壤蒸发数据以及附件8中降水等数据，建立模型对保持目前放牧策略不变情况下对2022年、2023年不同深度土壤湿度进行预测，并完成下表。

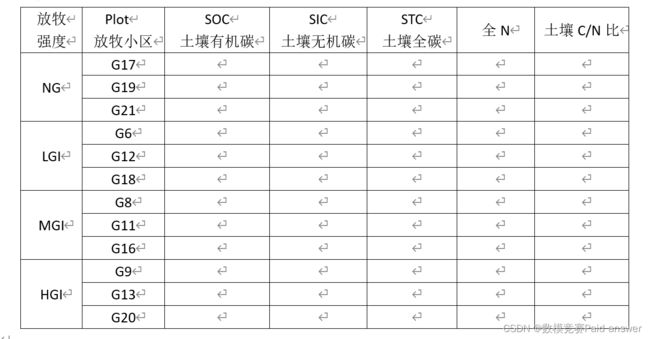
  问题3.从机理分析的角度，建立不同放牧策略（放牧方式和放牧强度）对锡林郭勒草原土壤化学性质影响的数学模型。并请结合附件14中数据预测锡林郭勒草原监测样地(12个放牧小区)在不同放牧强度下2022年土壤同期有机碳、无机碳、全N、土壤C/N比等值,并完成下表。

  问题4、利用沙漠化程度指数预测模型和附件提供数据（包括自己收集的数据）确定不同放牧强度下监测点的沙漠化程度指数值。并请尝试给出定量的土壤板结化定义，在建立合理的土壤板结化模型基础上结合问题3，给出放牧策略模型，使得沙漠化程度指数与板结化程度最小。
  问题5、锡林郭勒草原近10的年降水量（包含降雪）通常在300 mm ~1200 mm之间，请在给定的降水量（300mm，600mm、900 mm 和1200mm）情形下，在保持草原可持续发展情况下对实验草场内（附件14、15）放牧羊的数量进行求解，找到最大阈值。（注：这里计算结果可以不是正整数）
  问题6、在保持附件13的示范牧户放牧策略不变和问题4中得到的放牧方案两种情况下，用图示或者动态演示方式分别预测示范区2023年9月土地状态（比如土壤肥力变化、土壤湿度、植被覆盖等）。

整体求解过程概述(摘要)

  自 2003 年起，“退牧还草政策”逐渐进入人们视野，合理的草原放牧策略管理成为维护生物多样性、调节水土流失等现象的重要手段。在此背景下，本文研究一系列放牧强度对草原土壤物理性质、化学性质、植被生物量影响的诸多问题，广泛收集全球土壤数据、文献相关数据并进行数据处理和合并，综合运用微积分方程、多项式回归模型、OLS 普通最小二乘法算法、时间序列预测模型、决策树模型、RandomForest 回归模型、单变量回归诊断方法、粒子群算法、SHapley Additive exPlanation 特征影响分析、相关性分析、因子分析、变异系数法、熵值法、多目标进化算法等方法建立相关问题的数学模型，具体做法如下：
  针对问题一（放牧强度对土壤物理性质和植被生物量影响的数学模型），首先，从机理分析的角度厘清放牧策略对土壤湿度和植被生物量的影响关系和主要指标，采取逐步推理方式确定求解数学模型。然后，利用附件 3、4、5、6、9、10 等数据，研究降水量、蒸发量、叶面积指数、绿植覆盖率等主要指标与时间的关系。接着，采用 ARIMA 时序分析模型分别对降水量、蒸发量进行时序建模，并利用自相关/偏自相关系数、BIC、分位图进行最优模型选择和时序稳定性验证；同时，通过观察指标分布，采用多项式回归分析模型对叶面积指数、绿植覆盖率进行回归建模，利用 OLS 最小二乘法进行最优模型参数求解。最后，通过定性分析揭示不同放牧策略对土壤物理性质和植被生物量的影响关系。
  针对问题二（对 2022 年、2023 年不同深度土壤湿度进行预测），首先基于问题一从机理分析视角所建立的土壤湿度数学模型，明确土壤湿度的影响指标；然后，采用线性/非线性回归分析分别对关键影响指标(降水量、土壤蒸发量)按指定月份进行建模并预测；之后，基于降水量、土壤蒸发量对不同深度的土壤湿度的多重回归模型，挖掘三者间的相互作用关系；最后对 2022 年、2023 年不同深度土壤湿度进行预测，并对预测结果进行多维度分析，揭示了土壤湿度随降水量、土壤湿度的变化规律及其在不同月份和季度的演化特征和原因。
  针对问题三（放牧强度对土壤化学性质影响的数学模型及预测），首先，为了建立放牧强度对土壤化学性质影响的机理模型，根据已有方程模型，将具有实际意义的土壤化学性质（SOC、SIC 和全 N）与植物生物量的数据进行关联对应和数据均值处理并构建土壤化学性质同 Woodward 放牧与植物生长模型的等式。其次，根据问题一的方程求解方法，使用多项式回归求解与土壤化学性质随时间变化相关的系数并构建出数学模型。随后，构建 60 个基于 OLS 回归的不同放牧强度下不同小区土壤化学性质随时间变化的模型，使用CCPR 图、拟合图、偏回归图、模型残差图检验 OLS 回归模型建立的有效性并进行回归预测。最后，进行扩展研究，建立了决策树回归、线性回归、随机森林回归、AdaBoost 决策树回归、GradientBoost 回归、XGBoost 回归、CatBoost 回归、神经网络线性回归、LGBMBoost 回归累计 9 种回归模型预测不同放牧强度对土壤化学性质的影响，考虑影响每种土壤化学性质的最优模型并进行参数调优，确定影响每种土壤化学性质的最佳模型然后输入至可解释机器学习 SHapley Additive exPlanation 模型中，建立了不同放牧强度对土壤化学性质的影响机制。研究结果表明使用 OLS 回归能够很好地拟合不同放牧强度下各小区土壤化学性质的变化趋势，基于 SHAP 模型的影响机制建立，完美阐释了不同放牧强度对土壤化学性质影响的结果，验证了机器学习模型在相关研究中的有效性。
  针对问题四（沙漠化程度指数预测模型和土壤板结化），通过观察发现，现有的研究数据不能支撑该问题的解决，因此，本文广泛收集内蒙古水资源数据和全球土壤信息数据。针对沙漠化程度指数预测模型，根据现有文献，重新建立基于植物生长多样性因素、气象因素、地表与水资源因素、人文因素的沙漠化程度预警指标，整合附件 2、附件 6、附件 8和附件 15 及来自内蒙古政务网站的水资源数据，使用随机森林缺失值填充法和迭代插值法填补缺失数据，并充分考虑指标正负性影响，构建了基于因子分析法和变异系数法构建沙漠化程度指数公式；针对土壤板结化程度模型，随机收集来自 WoSIS 的 50 个地区全球土壤信息数据，基于熵值法构建全球土壤板结化程度公式，确定了土壤板结化的定量定义，并使用 flourish 可视化方法展现该 50 个地区土壤板结化程度；最后，基于 PSO 粒子群算法就沙漠化程度预测模型和土壤板结化程度模型进行最优求解，确定最优放牧策略为：当月降水量约为 45mm、平均气温约为 19 度时，采用轻牧方式。
  针对问题五（在特定降雨量条件下，预测草原可持续发展原则下的放牧标准羊数量最大值），通过对附件 8 中气候情况进行皮尔逊相关系数分析，显示降雨量与其他气候条件相关性较弱，可以作为独立变量。草原可持续发展原则是在保证生态环境良性健康发展中寻求经济利益的最大化，为此，本文定义了沙漠化指数、土壤板结化程度以及生物多样性指标来评估草原生态的良性发展，利用标准羊数量评估经济利益，并将该问题视为多目标优化问题。其中生物多样性指标使用α 多样性中的 ACE 指标计算，然后利用多项式回归建立了植物多样性同降水量、羊群数量的回归模型；经济利益通过分析附件 13，构建了每公顷经济收益同羊群数量的回归模型。最后，针对该多目标优化问题，使用融合回归模型的基于分解的多目标进化算法，在求解目标函数最优值，且满足约束条件的情况下，求解放牧标准羊数量的最大阈值。
  针对问题六（求解不同放牧策略下土地情况的变化），基于前五个问题研究的基础上，本文将问题六分解成四个子问题，分别建立不同放牧强度同土壤化学性质的回归模型，土壤化学性质、降雨量同土壤湿度的回归模型，植被指数同绿植覆盖率的回归模型，土壤湿度同绿植覆盖率的该回归模型，从而间接求解出不同放牧策略下土地肥力、土壤湿度、绿植覆盖率的变化情况。

模型假设：

  根据内蒙古锡林郭勒盟草原监测、调查数据情况和本题所给出的条件，本文作出如下假设：
  (1) 所给数据除给定限制条件外，没有其他外部因素的影响，且数据人工统计误差可以忽略。
  (2) 除了所给的附件数据之外，其他外部因素对土壤物理性质、化学性质等的影响可以忽略。
  (3) 对于需要按年或者月份统计的数据可以通过平均的方式计算。
  (4) 对于缺失数据可以通过平均插值法进行填充。
  (5) 在放牧策略确定的情况下，人类活动对土壤等各项指标产生影响可以忽略。
  (6) 所有参考模型、公式和文献都真实无误。

问题分析：

  从机理分析的角度，建立不同放牧策略（放牧方式和放牧强度）对锡林郭勒草原土壤物理性质（主要是土壤湿度）和植被生物量影响的数学模型。目前，不同放牧策略会对植被生物量产生影响，而生物量的变化关系到植被覆盖率和植被最大截流量。通过土壤-植被-大气系统的水平衡基本方程可知，植被截流率会影响到土壤土壤贮水变化量。因此，放牧强度会间接作用到土壤湿度变化。解析土壤湿度模型，需要获取影响土壤贮水变化量的降水量、蒸发量、植被截流率和植被覆盖率等因素。

  问题二需要建立一些模型对保持目前放牧策略不变情况下对 2022 年、2023 年不同深度土壤湿度进行预测。根据问题一中土壤湿度与降水量、土壤蒸发量、植被截流量、水毛管上升量、土壤水渗透量和径流量等有关，因此在保持放牧策略不变的情况下，植被生物量确定（根据问题一放牧方式与植被生物量关系公式）。由于植被的截流量与植被生物量有关其中，假设内蒙古土壤水毛管上升量和土壤水渗透量为特定量，同时在草原中径流量的出入相等。因此，因此影响土壤湿度的关键指标为土壤蒸发量和降水量。预测 2022 年、2023 年不同深度土壤湿度，首先预测土壤蒸发量和降水量，进而根据拟合的土壤蒸发量和降水量对土壤湿度的关系，获取指定时间的土壤湿度数据。

  问题三分为两个子问题，第一个子问题同问题一一样需要从机理分析角度建立不同放牧策略对锡林郭勒草原土壤化学性质影响，为更近一步探究放牧策略对土壤化学性质的影响方向，我们建立放牧策略对土壤化学性质影响模型；第二子问题需要完成对不同放牧策略下 2022 年各类土壤化学性质的预测。

  问题四包括三个子问题，各个子问题分析如下：
  子问题一：要求利用沙漠化程度指数预测模型确定不同放牧强度下监测点的沙漠化程度。针对该问题，首先需要整理确定影响沙漠化程度指数的变量，其次需要确定沙漠化指数的各变量的系数。根据题目提供的沙漠化程度指数指标，我们发现题目所提供的数据集有限，且难以收集到更多其他相关数据，因此，在该问题中，我们根据已有文献重新定义影响沙漠化程度的相关指标，然后使用变异系数法确定各指标的系数，进而来预测不同放牧强度下监测点的沙漠化程度。在该部分涉及到附件 15、附件 8、附件 6 和附件 2 等相关数据。
  子问题二：子问题二需要给出定量的土壤板结化定义和建立合理的土壤板结化模型。由于题目中没有更多相关的数据，因此，首先我们从其他网站上收集关于土壤有机物、土壤湿度和土壤的容重的数据，然后使用熵值法确定各指标的权重系数，进而建立土壤板结化模型。
  子问题三：给出放牧策略模型，使得沙漠化程度指数与土壤板结化程度最小。考虑到根据子问题和子问题二可以求解出关于沙漠化程度指数和土壤板结化的公式，基于这两个公式，使用粒子群算法进行求解。随机森林缺失值填充法和 IterativeImputer 多变量缺失值法。

  问题五需在给定降水量的情形下，在保持草原可持续发展情况下找到实验草场内放牧羊数量的最大阈值。现代草地资源经营的可持续发展原则是在保证生态环境良好健康发展中寻求经济利益的最大化，依据问题四，我们将生态环境良好定义为草场土壤板结化程度和沙漠化程度小，且生物多样性丰富。一昧得追求经济效益即扩大草场放牧羊的数量，将对生态环境造成很大影响，为实现草原资源的可持续发展，需在土壤板结化、沙漠化、生物多样性以及经济效益中进行权衡，因此我们将该问题看作为一个多目标优化问题，并主要利用融合回归模型的多目标优化算法来获取在保持草原可持续发展情况下的放牧羊数量的最大阈值。

  该问题需要预测在示范区牧户放牧策略不变和问题四得到的放牧方案两种情况下，示范区 2023 年 9 月的土壤肥力、土壤湿度、植被覆盖等土地状态的情况。为求解该问题，我们利用了问题一、问题三得到的放牧强度同植被覆盖率模型和放牧强度同土壤情况模型来进行计算。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

部分Python程序如下:

import pandas as pd
caoyuan=pd.read_excel('D:\\DataSet\\19届研究生数模竞赛\\2022年E题数据\数据集\监测点
数据\\附件14：内蒙古自治区锡林郭勒盟典型草原不同放牧强度土壤碳氮监测数据集
（2012年8月15日-2020年8月15日）\\内蒙古自治区锡林郭勒盟典型草原不同放牧强度土壤
碳氮监测数据集（2012年8月15日-2020年8月15日）.xlsx')
caoyuan=caoyuan[['intensity','SOC土壤有机碳','SIC土壤无机碳','STC土壤全碳','全氮N','土
壤C/N比']]
caoyuan.head()
from sklearn.preprocessing import OneHotEncoder
caoyuanH=pd.get_dummies(caoyuan, prefix=['inten','year','plot'],columns=['intensity','year','plot'])
import sklearn
#机器学习算法模型
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeRegressor
#准确率，精确率，召回率，f1
from sklearn.metrics import
accuracy_score,precision_score,recall_score,f1_score,classification_report
import xgboost as xgb
import joblib
from xgboost import XGBRegressor
from sklearn.model_selection import train_test_split
X = caoyuanH.drop(['SOC','SIC','STC','N','CN'],axis=1)
X
# X=caoyuanH[['SOC土壤有机碳','SIC土壤无机碳','STC土壤全碳','全氮N','土壤C/N比']]
Y=caoyuanH['SOC']
test_size = 0.2
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=test_size, random_state=123)
from sklearn.metrics import mean_squared_error,mean_absolute_error,r2_score
modelDecision= DecisionTreeRegressor()
modelDecision.fit(X_train, y_train)
# 对测试集做预测
y_pred = modelDecision.predict(X_test)

predictions = [round(value) for value in y_pred]
# 评估预测结果
MAE=mean_absolute_error(y_pred, y_test)
MSE=mean_squared_error(y_pred, y_test)
print(MAE,MSE)
modelMLP= MLPRegressor()
modelMLP.fit(X_train, y_train)
# 对测试集做预测
y_pred =modelMLP.predict(X_test)
predictions = [round(value) for value in y_pred]
# 评估预测结果
MAE=mean_absolute_error(y_pred, y_test)
MSE=mean_squared_error(y_pred, y_test)
print(MAE,MSE)
from sklearn import linear_model
modelLinear=linear_model.LinearRegression()
modelLinear.fit(X_train, y_train)
# 对测试集做预测
y_pred = modelLinear.predict(X_test)
predictions = [round(value) for value in y_pred]
# 评估预测结果
MAE=mean_absolute_error(y_pred, y_test)
MSE=mean_squared_error(y_pred, y_test)
print(MAE,MSE)
modelRandom= RandomForestRegressor()
modelRandom.fit(X_train, y_train)
# 对测试集做预测
y_pred = modelRandom.predict(X_test)
predictions = [round(value) for value in y_pred]
# 评估预测结果
MAE=mean_absolute_error(y_pred, y_test)
MSE=mean_squared_error(y_pred, y_test)
print(MAE,MSE)
modelADA= AdaBoostRegressor()
modelADA.fit(X_train, y_train)
# 对测试集做预测
y_pred =modelADA.predict(X_test)
predictions = [round(value) for value in y_pred]
# 评估预测结果
MAE=mean_absolute_error(y_pred, y_test)
MSE=mean_squared_error(y_pred, y_test)
print(MAE,MSE)
modelGradient= GradientBoostingRegressor()
modelGradient.fit(X_train, y_train)
# 对测试集做预测
y_pred =modelGradient.predict(X_test)
predictions = [round(value) for value in y_pred]
# 评估预测结果
MAE=mean_absolute_error(y_pred, y_test)
MSE=mean_squared_error(y_pred, y_test)
print(MAE,MSE)
modelXGB= XGBRegressor()
modelXGB.fit(X_train, y_train)
# 对测试集做预测
y_pred =modelXGB.predict(X_test)
predictions = [round(value) for value in y_pred]
# 评估预测结果
MAE=mean_absolute_error(y_pred, y_test)
MSE=mean_squared_error(y_pred, y_test)
print(MAE,MSE)
modelCat= CatBoostRegressor()
modelCat.fit(X_train, y_train)
# 对测试集做预测
y_pred =modelCat.predict(X_test)
predictions = [round(value) for value in y_pred]
# 评估预测结果
MAE=mean_absolute_error(y_pred, y_test)
MSE=mean_squared_error(y_pred, y_test)
print(MAE,MSE)
modelLGB= lgb.LGBMRegressor()
modelLGB.fit(X_train, y_train)
# 对测试集做预测
y_pred =modelLGB.predict(X_test)
predictions = [round(value) for value in y_pred]
# 评估预测结果
MAE=mean_absolute_error(y_pred, y_test)
MSE=mean_squared_error(y_pred, y_test)
print(MAE,MSE)

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error, median_absolute_error
from sklearn.preprocessing import PolynomialFeatures
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
import pandas as pd
df = pd.read_excel(r'Data/f8_weather_3.xls', sheet_name='10月')
# 生成测试数据:
#nSample = 100
x = df['月份'].values # = np.linspace(0, 10, nSample) # 起点为 0，终点为 10，均分为
nSample个点
#e = np.random.normal(size=len(x)) # 正态分布随机数
y = df['降水量'].values #= 2.36 + 1.58 * x + e # y = b0 + b1*x1
# 按照模型要求进行数据转换：输入是 array类型的 n*m 矩阵，输出是 array类型的 n*1
数组
x = x.reshape(-1, 1) # 输入转换为 n行 1列（多元回归则为多列）的二维数组
y = y.reshape(-1, 1) # 输出转换为 n行1列的二维数组
# print(x.shape,y.shape)
# 定义多项式回归, degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=2)
# 特征处理
x_poly = poly_reg.fit_transform(x)
# 定义回归模型
reg = LinearRegression()
reg.fit(x_poly, y)
#plt.plot(x, y, 'b.')
#plt.plot(x, reg.predict(x_poly), 'r')
#plt.show()
plt.style.use("seaborn-deep")
# 绘图：原始数据点，拟合曲线
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x, y, 'o', label="data") # 原始数据
ax.plot(x, reg.predict(x_poly), 'r-', label="OLS") # 拟合数据
ax.legend(loc='best') # 显示图例
ax.legend(loc='best') # 显示图例
plt.title('降水量')
plt.grid(ls='--')
plt.savefig('降水量_duo10.jpg')
plt.show()
# 输出回归结果 XUPT
print('回归截距: w0={}'.format(reg.intercept_)) # w0: 截距
print('回归系数: w1={}'.format(reg.coef_)) # w1,..wm: 回归系数
# 回归模型的评价指标 YouCans
print('R2 确定系数：{:.4f}'.format(reg.score(x_poly, y))) # R2 判定系数
print('均方误差：{:.4f}'.format(mean_squared_error(y, reg.predict(x_poly)))) # MSE 均方误
差
print('平均绝对值误差：{:.4f}'.format(mean_absolute_error(y, reg.predict(x_poly)))) # MAE
平均绝对误差
print('中位绝对值误差：{:.4f}'.format(median_absolute_error(y, reg.predict(x_poly)))) # 中
值绝对误差

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可