拓扑排序（不整虚的 实例带你分析 含indegree）

今天阿尼亚也在好好学习！（干饭bushi）

一键跳跃按钮：

复杂度:

需要什么：准备工作：

逻辑化代码（汉字代码双混 便于理解）（栈的操作放在了结尾）：

上实例：写出此DAG的一个拓扑排序并且分析indegree print 和 栈中的元素究竟怎么变化的

round 1：

round 2：

round 3：

拓扑需要的栈操作

准备工作：

初始化栈 （将来定义时还得传地址）

入栈操作 （注意分清楚top的大小和capacity的关系）

栈的判空

弹出栈

取出栈顶元素

最后找一个练习题练手：

---

 

复杂度:

时间复杂度：

O(V+E) 每一个顶点和边都会被操作

若邻接矩阵表示图：则需要O(V ^2)

需要什么：准备工作：

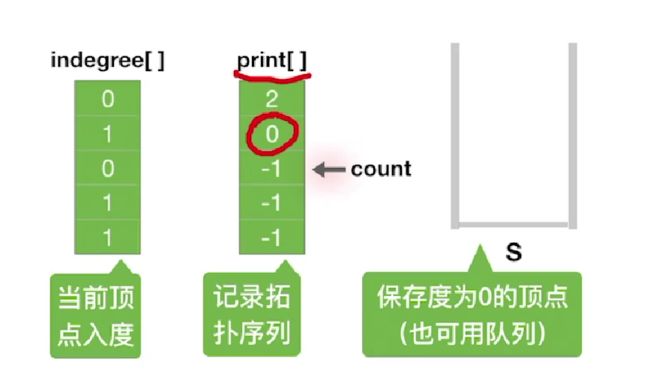
一、indegree数组 记录每个顶点入度情况

二、print数组 1、记录拓扑序列2、记录好之后 将来一个for循环直接嘎嘎输出 所以既是记录也是输出

三、还得定义一个栈 : 所有所有所有（重要的事情说三遍）入度为0的节点都入栈

（1.一出生入度为0 2.通过for循环--度删边之后的操作使得节点的度为0 ）这俩种情况的节点都得入栈

四、需要一个count 用来计数 且count的作用和print绑定 1.记录当前已经输出（出栈pop）的顶点数 2.利用count寻找print数组下标

逻辑化代码（汉字代码双混 便于理解）（栈的操作放在了结尾）：

#define vexnum 5
bool Topologicalsort(Graph G) {
	int indegree[10] = {0}; int print[10] = {0};
	Stack st;
	StackInit(&st);
	for (int i = 0; i < vexnum; i++) {
		if (indegree[i] == 0) StackPush(&st, i); //将所有入度为0的顶点入栈
		int count = 0; // 作用已写
		while (!StackEmpty(&st)) { // 栈不空 则存在入度为0的顶点 就要操作
			StackPop(&st); // 栈顶元素出栈 每个节点都会处理一次
			print[count] = i; count++;//记录弹出元素
			for (、、、) {
				v = p->adjvex;
				if (!(--indegree[v])) StackPush(&st, v);
			}//用来删边 少度的小for
		}//用来处理栈中无元素的while
	}//大for 直到图中节点全无才结束
	//最后判断 若 count小于 顶点数 就是排序失败 图中含有回路 反之则正确
}

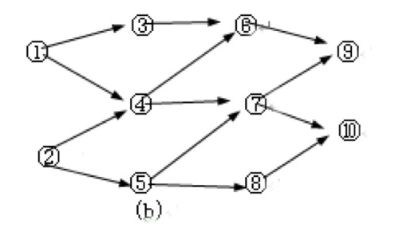
上实例：写出此DAG的一个拓扑排序并且分析indegree print 和 栈中的元素究竟怎么变化的

round 1：

0号节点的入度为0 1号节点的入度为1 二号节点的入度为0 3号节点的入度为2 4号节点的入度为2

不光可以从图中看 有几个指向顶点的弧 indegree就是记录这个东西的 就可以一一对应

print全部初始化成-1

将所有入度为0的顶点进栈 ：

if (indegree[i] == 0) StackPush(st, i);

现在需要对栈顶元素出栈 2号弹出 且count指向的位置是2 且进行count++

while (!S = StackEmpty(st)) {
		pop(st, i);
		print[count] = i; count++;
		for(,,,)// 处理和被弹出节点 i 所有相连接的节点 令他们的度减一 逻辑上就是删边{
  	度减减
  	if(度==0) StackPush(st, i);
		}// for
}//while

将所有被弹出顶点所指向的顶点的入度减一（逻辑上就是：删除二号节点与其余节点相连的边）

并且将入度为0的顶点压入栈s if(度==0) StackPush(st, i);

round 2：

此时栈依然是非空的

则依然要弹出（这是一个while循环）

此时0被弹出 则将0的值赋给print数组 同时count++；

接下来要0号与所连节点进行删边操作了 将1号节点的度减一

这导致1号节点没有前驱节点了 入度为0 嘎嘎入栈

、

此时从删度的小for循环跳出 跳到了大的while循环当中去 那么继续将弹出的值赋给print数组

将1号存储好之后 还得进行小for循环 那么就意味着 1号节点所指的3号节点的入度再次减少

round 3：

现在从indegree可以看出 3号选手的入度为0 令其入栈

进入while循环 将3号节点出栈 记录在count中 并且count++

对被弹出3号所连节点的入度进行减一的操作 这就导致4号节点的入度为0 令其入度

现在又从小for循环跳出到了while循环当中去 将4号节点出栈 并且记录在print数组中

由于4号节点没有后继 那么while循环结束了 此时count的结果是5

特殊的 ： 要是 count的值小于顶点个数 这就说明出现了有环图 而不再是DAG 有向无环图

拓扑需要的栈操作

准备工作：

typedef struct Stack {
	STDataType* a;
	int top;
	int capacity;
}ST;

初始化栈 （将来定义时还得传地址）

void StackInit(ST* ps) {
	assert(ps);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}

入栈操作 （注意分清楚top的大小和capacity的关系）

void StackPush(ST* ps, STDataType x) {
	assert(ps);
	//最担心的就是出现了top和capacity相等的情况
	if (ps->top == ps->capacity) {
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;//要是原来的值不等于0的话 就直接2倍扩大 避免扩多浪费、
		//realloc函数 void*reallocc(void* beforep,newsize) 那么 首先得强制类型转换 然后写上开辟空间的ps—>a 接着写上新空间的字节数
		STDataType* tmp = (STDataType*)realloc(ps->a, newCapacity * sizeof(STDataType));
		assert(tmp);// 担心创建失败
		//别忘了将tmp和原先的建立联系 错因
		ps->a=tmp;//将新创建的空间建立好联系
		ps->capacity = newCapacity;
	}
	//若是没有出现满栈问题的话
	ps->a[ps->top] = x; // ps->a 是形容的指针 但是a中要是有元素的话 就是元素本身了
	ps->top++;
}

栈的判空

bool StackEmpty(ST* ps) {
	assert(ps);
	return ps->top == 0;
}

弹出栈

void StackPop(ST* ps) {
	assert(ps);
	assert(!StackEmpty(ps));
	--ps->top;
}

取出栈顶元素

//取出栈顶元素
STDataType StackTop(ST* ps) {
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->a[ps->top - 1];
}

最后找一个练习题练手：