【C++】AVL树的插入操作实现以及验证是否正确（带平衡因子）

---

前言

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：
1.它的左右子树都是AVL树
2.左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在$O(lo{g}_{2}n)$，搜索时间复杂度O($lo{g}_{2}n$)。

一、AVL树结点的定义

template<class K,class V>
//我们这里用键值的数据类型来举例
struct AVLTreeNode {
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;//（父结点）
	int _bf;//（平衡因子大小）

	AVLTreeNode(const pair<K, V>& kv)
		//构造函数
		:_kv(kv),
		_left(nullptr),
		_right(nullptr),
		_parent(nullptr),
		_bf(0)
	{}
};

二、AVL树的插入（Insert）

AVL树的插入过程可以分为两步：

1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子

插入完整代码：

typedef AVLTreeNode<K, V> Node;
bool Insert(const pair<K, V>& kv) {
		
		if (_root == nullptr) {
			//若为空树就先建立结点
			_root = new Node(kv);
			return  true;
		}
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur) {
			//寻找要插入结点的父亲的位置
			if (cur->_kv.first < kv.first) {
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first) {
				parent = cur;
				cur = cur->_left;
			}
			else {
				return false;
			}
		}
		cur = new Node(kv);
		//找到要插入结点父亲后，寻找插入其左边还是右边
		if (parent->_kv.first < kv.first) {
			parent->_right = cur;
		}
		else {
			parent->_left = cur;
		}
		cur->_parent = parent;
		while (parent) {//更新平衡因子
			if (parent->_left == cur) {
				parent->_bf--;
			}
			else {
				parent->_bf ++ ;
			}
			// 更新后检测双亲的平衡因子
			if (parent->_bf == 0) {
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1) {
				// 插入前双亲的平衡因子是0，插入后双亲的平衡因为为1 或者 -1 ，说明以双亲
				//为根的二叉树的高度增加了一层，因此需要继续向上调整
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2) {
				// 双亲的平衡因子为正负2，违反了AVL树的平衡性，需要对以parent
                // 为根的树进行旋转处理
				if (parent->_bf == 2 && cur->_bf == 1) {
					RotateL(parent);//左单旋
				}
				else if (parent->_bf == -2 && cur->_bf == -1) {
					RotateR(parent);//右单旋
				}
				else if (parent->_bf == 2 && cur->_bf == -1) {
					RotateRL(parent);//双旋
				}
				else if (parent->_bf == -2 && cur->_bf == 1) {
					RotateLR(parent);//双旋
				}
				break;
			}
			else {
				assert(false);
			}
			
		}
		return true;
	}

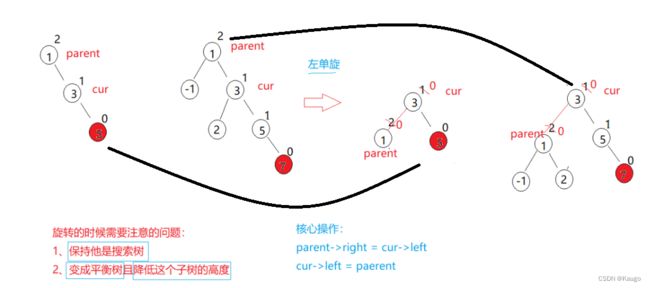
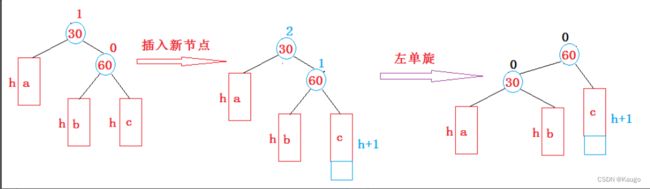
1.左单旋（RotateL）

 void RotateL(Node* parent) {
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		parent->_right = curleft;//  核心操作
		if (curleft) {
			//因为curleft可能为空
			curleft->_parent = parent;
		}
		Node* ppnode = parent->_parent;
		//提前记录下父结点的父亲
		cur->_left = parent;//     核心操作
		parent->_parent = cur;
		if (ppnode == nullptr) {
			//判断原先parent是否为根节点
			//因为根节点的父亲为空
			_root = cur;
			cur->_parent = nullptr;
		}
		else {
			 //说明parent不为根节点
			//parent可能为ppnode的左或者右子树，改变ppnode的指向
			if (ppnode->_left == parent) {
				ppnode->_left = cur;
			}
			else {
				ppnode->_right = cur;
			}
			cur->_parent = ppnode;
		}
		parent->_bf = cur->_bf = 0;
		// 根据调整后的结构更新部分节点的平衡因子
	} 

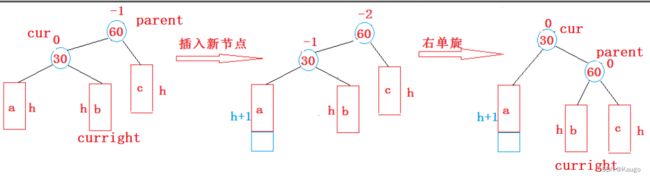
2.右单旋（RotateR）

 void RotateR(Node* parent) {
		Node* cur = parent->_left;
		Node* curright = cur->_right;
		parent->_left = curright;
		if (curright) {
			//因为curleft可能为空
			curright->_parent = parent;
		}
		cur->_right = parent;
		Node* ppnode = parent->_parent;
		parent->_parent = cur;
		if (ppnode == nullptr) {
			//判断原先parent是否为根节点
			//因为根节点的父亲为空
			_root = cur;
			cur->_parent = nullptr;
		}
		else {
			//说明parent不为根节点
		   //parent可能为ppnode的左或者右子树，改变ppnode的指向
			if (ppnode->_left == parent) {
				ppnode->_left = cur;
			}
			else {
				ppnode->_right = cur;
			}
			cur->_parent = ppnode;
		}
		parent->_bf = cur->_bf = 0;
		// 根据调整后的结构更新部分节点的平衡因子
	} 

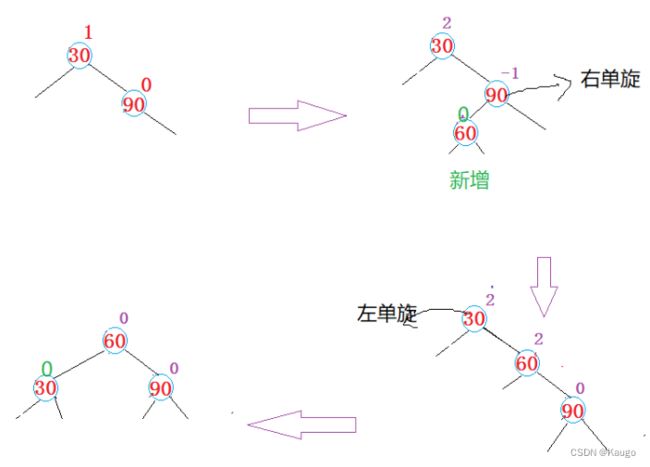
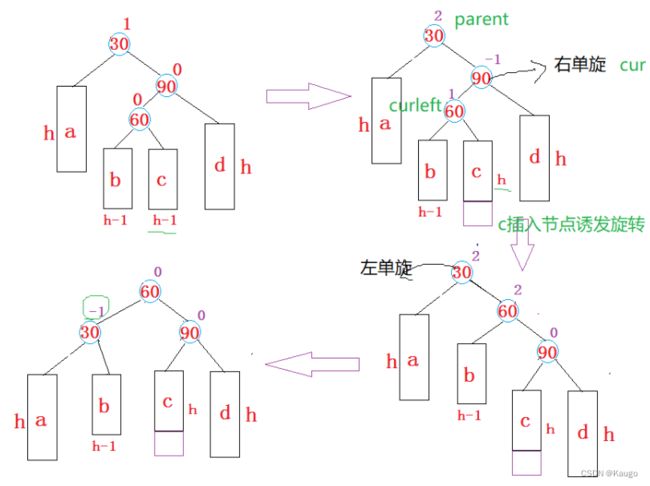
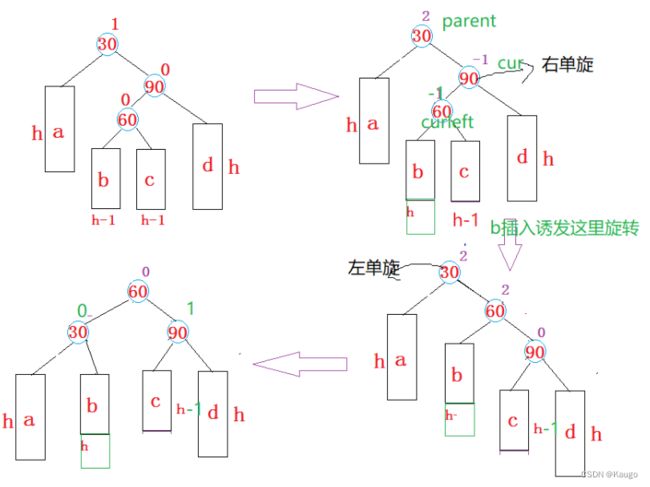
3.先右单旋再左单旋（RotateRL）

以cur为旋转点进行右旋，以parent为旋转点进行左旋，之后进行平衡因子的修改

 void RotateRL(Node* parent) {
		Node* cur = parent->_right;
		Node* curleft = cur->_left;
		int bf = curleft->_bf;
		// 旋转之前，保存curleft的平衡因子，旋转完成之后，需要根据该平衡因子来调整其他节
		//点的平衡因子
		RotateR(cur);
		RotateL(parent);
		if (bf == 0) {
			cur->_bf = 0;
			curleft->_bf = 0;
			parent->_bf = 0;
		}
		else if (bf == 1) {
			cur->_bf = 0;
			curleft->_bf = 0;
			parent->_bf = -1;
		}
		else if (bf == -1)
		{
			cur->_bf = 1;
			curleft->_bf = 0;
			parent->_bf = 0;
		}
		else
		{
			assert(false);
		}
	} 

1.保存的bf为0

2.保存的bf为1

3.保存的bf为-1

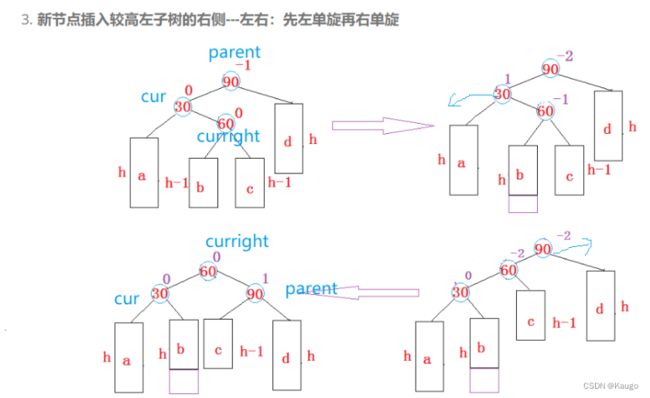
4.先左单旋再右单旋（RotateLR）

以cur为旋转点进行左旋，以parent为旋转点进行右旋，之后进行平衡因子的修改

 void RotateLR(Node* parent) {
		Node* cur = parent->_left;
		Node* curright = cur->_right;
		int bf = curright->_bf;
		// 旋转之前，保存curright的平衡因子，旋转完成之后，需要根据该平衡因子来调整其他节
		//点的平衡因子
		RotateL(cur);
		RotateR(parent);
		if (bf == 0) {
			cur->_bf = 0;
			parent->_bf = 0;
			curright->_bf = 0;
		}

		else if (bf == -1)
		{
			parent->_bf = 1;
			cur->_bf = 0;
			curright->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = 0;
			cur->_bf = -1;
			curright->_bf = 0;
		}
		else {
			assert(false);
		}
	} 

三、AVL树的验证

验证其为平衡树关键点：
1.每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
2.节点的平衡因子是否计算正确

int  Height(Node* root) {
		if (root == nullptr) {
			return 0;
		}
		int left =  Height(root->_left);
		int right =  Height(root->_right);
		return left > right ? left + 1 : right + 1;
	}

	bool IsBalance() {
		return IsBalance(_root);
	}
	bool IsBalance(Node* root) {
		if (root == nullptr) {
			return true;
		}
		int left = Height(root->_left);
		int right = Height(root->_right);
		if (right - left != root->_bf) {//节点的平衡因子是否计算正确
			cout << "平衡因子异常" << root->_kv.first << "=>" << root->_bf << endl;
			return false;
		}
		//每个节点子树高度差的绝对值不超过1
		//之后在验证左右子树
		return abs(right-left)<2&&IsBalance(root->_left) && IsBalance(root->_right);
	}