dp(2) - 最长上升子序列模型
目录 :
简论
最长上升子序列
链接 :
题面:
思路 :
代码 :
最长递增子序列
链接 :
题面 :
编辑
思路 :
代码:
怪盗基德的滑翔翼
链接 :
题面 :
思路 :
代码 :
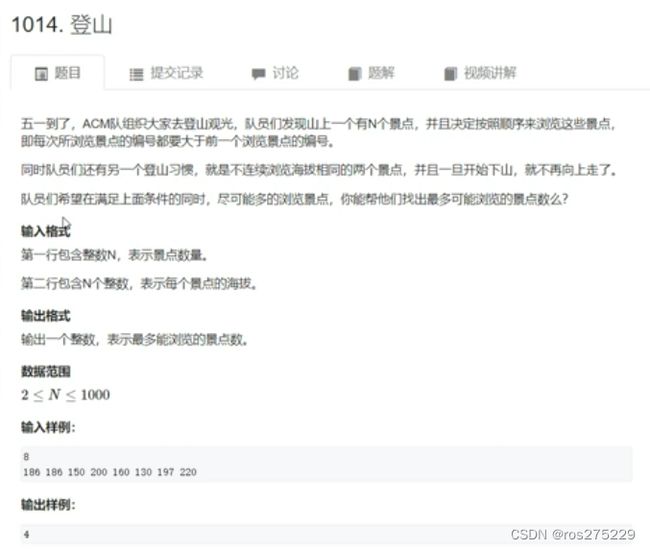
登山
原题链接 :
题面 :
编辑
思路 :
代码 :
合唱队形
链接 :
题面 :
编辑
思路 :
代码 :
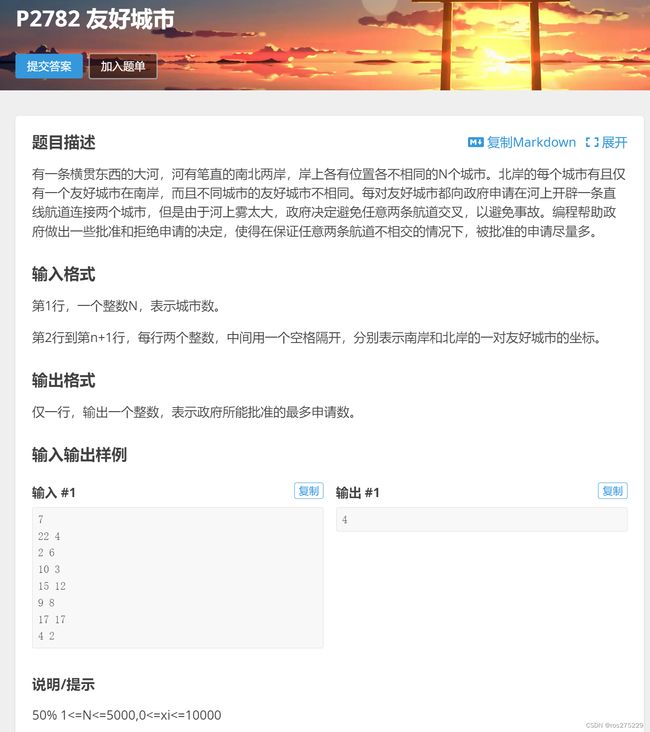
友好城市
链接 :
题面 :
编辑
思路 :
代码 1:
代码(优化)
1016.最大上升子序列和
链接 :
题面 :
思路 :
代码 :
导弹拦截
链接 :
题面 :
思路 :
代码 [O(n^2)]:
代码 [O(nlogn)] :
187.弹道防御系统
链接 :
思路 :
代码 :
272.最长上升公共子序列
原题链接 :
思路 :
代码 :
简论
最长上升子序列(Longest Increasing Subsequence),简称LIS,也有些情况求的是最长非降序子序列,二者区别就是序列中是否可以有相等的数。假设我们有一个序列 b i,当b1 < b2 < … < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2, …, aN),我们也可以从中得到一些上升的子序列(ai1, ai2, …, aiK),这里1 <= i1 < i2 < … < iK <= N,但必须按照从前到后的顺序。比如,对于序列(1, 7, 3, 5, 9, 4, 8),我们就会得到一些上升的子序列,如(1, 7, 9), (3, 4, 8), (1, 3, 5, 8)等等,而这些子序列中最长的(如子序列(1, 3, 5, 8) ),它的长度为4,因此该序列的最长上升子序列长度为4。
最长上升子序列
链接 :
-
最长上升子序列 - AcWing
题面:
给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。
输入格式 第一行包含整数 N。
第二行包含 N 个整数,表示完整序列。
输出格式 输出一个整数,表示最大长度。
数据范围 : 1≤N≤1000,−109≤数列中的数≤109 输入样例: 7 3 1 2 1 8 5 6 输出样例: 4
思路 :
用f[i]表示以a[i]结尾的最长上升子序列的长度;
详情见图;
代码 :
#include
using namespace std;
const int N = 1010;
int n,a[N],f[N];
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
f[i] = 1;
for(int j=1;j 最长递增子序列
链接 :
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
题面 :
思路 :
同上
代码:
class Solution {
public:
int lengthOfLIS(vector& nums) {
int n = nums.size();
int res = 0;
vector dp(n+1);
for(int i=1;i<=n;i++){
dp[i] = 1;
for(int j=1;j 怪盗基德的滑翔翼
链接 :
怪盗基德的滑翔翼 - AcWing
题面 :
题目给定一个长度为 n的一维数组 w[n],表示每个楼房的高度,
怪盗基德可以选定任意一个楼房,作为他的起始位置
他可以选择向左或向右出发直到边界,途中不能改变方向
题目要求我们找出一条路径,使得他飞行的路线上,经过的高度递减的楼房子序列长度最大
输出该子序列的长度
思路 :
模型 :
我们只需要求一遍最长上升子序列,再求一遍最长下降子序列,这两者中的最小值就是答案。
代码 :
#include
using namespace std;
const int N=110;
int a[N],f[N];
int main(){
int t;
cin>>t;
while(t--){
int res=0,n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;ja[i])
f[i]=max(f[i],f[j]+1);
res = max(res,f[i]);
}
cout< 登山
原题链接 :
登山 - AcWing
题面 :
思路 :
-
按照编号递增的顺序来浏览 : 必须时子序列
-
相邻的两个景点不能相同 :
-
开始下降,就不能开始上升了
-
求最多能够浏览多少景点
题目也就是求满足下面形状子序列的最大长度 :
然后对于这个求解,先正向求一个LIS存于f(n)中,然后反向求一个LIS存于g(n)中,每个点的关于问题的最大长度为f[i]+g[i]-1,然后遍历求得最大值即可。
代码 :
#include
using namespace std;
const int N = 1010;
int n,h[N],f[N],g[N],res;
int main(){
cin >> n;
for(int i = 1;i <= n;i++) scanf("%d",&h[i]);
// 正
for(int i = 1;i <= n;i++){
f[i] = 1;
for(int j = 1;j <= n;j++)
if(h[j] < h[i]) f[i] = max(f[i],f[j]+1);
}
// 反
for(int i = n;i >= 1;i--){
g[i] = 1;
for(int j = n;j >= i;j--)
if(h[j] < h[i]) g[i] = max(g[i],g[j]+1);
}
for(int i = 1;i <= n;i++) res = max(res,f[i]+g[i]-1);
cout << res< 合唱队形
链接 :
-
482. 合唱队形 - AcWing题库
-
合唱队形_牛客网
题面 :
思路 :
与上题思路一摸一样,最后输出n-res即可
代码 :
#include
using namespace std;
const int N=1010;
int a[N],f[N],g[N];
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){//求以每个点结尾的最长上升子序列
f[i]=1;
for(int j=1;ji;j--){
if(a[j] 友好城市
链接 :
-
友好城市 - AcWing
-
友好城市 - 洛谷
题面 :
思路 :
-
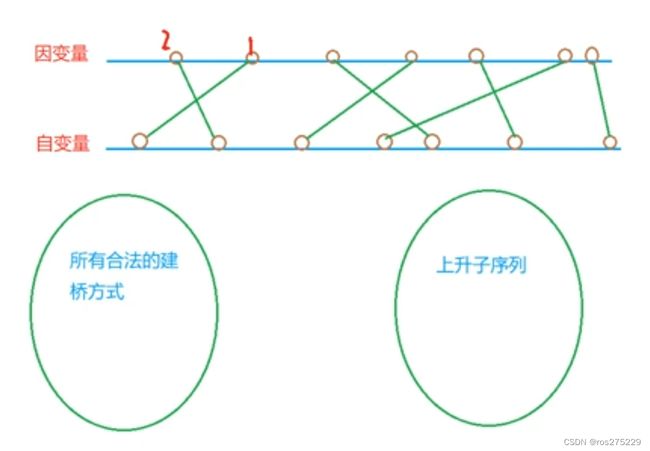
先将所有的信息读入到pair中
对于两岸的城市相互对应,要求建的桥不能相交,求最多能建多少座桥;
-
先对整个pair数组进行排序。
-
然后就可以转化为LIS问题了;
代码 1:
对于acwing中,n<=5000,n*n也不会超时,可以直接暴力LIS求解
#include
#include
using namespace std;
const int N=5050;
typedef pair PII;
PII a[N];
int f[N];
int main(){
int n; cin>>n;
for(int i=1;i<=n;i++) cin>>a[i].first>>a[i].second;
sort(a+1,a+n+1);
int res = 0;
for(int i=1;i<=n;i++){//求以每个点结尾的最长上升子序列
f[i]=1;
for(int j=1;j 代码(优化)
对于洛谷中的n<=2e5,那么暴力的LIS肯定是不行的;
要加上二分来优化,具体请看下面代码 :
#include
#include
using namespace std;
const int N=2e5+10;
typedef pair PII;
PII a[N];
int f[N];
int main(){
int n,res = 0; cin>>n;
for(int i=0;i>a[i].first>>a[i].second;
sort(a,a+n);
int len = 0;
for (int i = 0; i < n; i ++ )
{
int l = 0, r = len;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (f[mid] < a[i].second) l = mid;
else r = mid - 1;
}
len = max(len, r + 1);
f[r + 1] = a[i].second;
}
res = len ;
cout< 二分优化具体请看 : 最长上升子序列优化(贪心+二分)(超级详细的讲解)_最长上升子序列二分优化_Turing_Sheep的博客-CSDN博客
LIS二分优化模板 :
int len = 0;
for (int i = 0; i < n; i ++ )
{
int l = 0, r = len;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (q[mid] < a[i]) l = mid;
else r = mid - 1;
}
len = max(len, r + 1);
q[r + 1] = a[i];
}1016.最大上升子序列和
链接 :
活动 - AcWing
题面 :
一个数的序列 bi,当 b1 对于给定的一个序列(a1,a2,…,aN),我们可以得到一些上升的子序列(ai1,ai2,…,aiK),这里1≤i1 比如,对于序列(1,7,3,5,9,4,8),有它的一些上升子序列,如(1,7),(3,4,8)等等。 这些子序列中和最大为18,为子序列(1,3,5,9)的和。 你的任务,就是对于给定的序列,求出最大上升子序列和。 注意,最长的上升子序列的和不一定是最大的,比如序列(100,1,2,3)的最大上升子序列和为100,而最长上升子序列为(1,2,3)。 输入格式 输入的第一行是序列的长度N。 第二行给出序列中的N个整数,这些整数的取值范围都在0到10000(可能重复)。 输出格式 数据范围 输入样例: 输出样例: 和最长上升子序列相类似,只需改变一些条件就行了; f[i]代表以a[i]结尾的最大上升子序列和; 导弹拦截 - AcWing 导弹拦截 _ 牛客 [NOIP1999 普及组] 导弹拦截 - 洛谷 题目描述 : 某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。 输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。 输入格式 一行,空格隔开的若干个正整数。 输出格式 两行,每行一个整数。 第一个整数表示最多能拦截的导弹数; 第二个整数表示要拦截所有导弹最少要配备的系统数。 数据范围与提示 输入样例 输出样例 对于第一问 : 一个LIS即可解决,求最长下降子序列的长度即可 对于第二问 : 采用贪心的思路: 从前往后扫描每个数,对于每个数: 情况一 : 如果现有的子序列的结尾都小于当前数,则创建新的子序列 情况二 : 将当前数放到结尾大于等于它的最小的子序列后面 : 选择对后面造成最小影响的选法(可以理解留下高度较大的来防范后面的导弹); 贪心的证明 : 假设最优解对应的方案和当前方案不同 第二问就是问这个序列最少可以划分为多少个非递增序列,根据Dilworth定理,我们只需求最长上升子序列的长度就是答案。 Dilworth : Dilworth定理,一言以蔽之,偏序集能划分成的最少的全序集个数等于最大反链的元素个数 关于Dilworth定理 : Dilworth定理 关于dilworth相关题的总结 : 最小链覆盖——Dilworth定理_·马克图布·的博客-CSDN博客 对于洛谷的要求O(nlogn),那么就要用二分来优化; 187. 导弹防御系统 上一题 套个dfs 最长公共上升子序列 这一题是 最长上升子序列 + 最长公共子序列 fi代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合; fi的值等于该集合的子序列中长度的最大值 首先依据公共子序列中是否包含a[i],将fi所代表的集合划分成两个不重不漏的子集: 不包含a[i]的子集,最大值是fi - 1; 包含a[i]的子集,将这个子集继续划分,依据是子序列的倒数第二个元素在b[]中是哪个数: 子序列只包含b[j]一个数,长度是1; 子序列的倒数第二个数是b[1]的集合,最大长度是fi - 1 + 1; … 子序列的倒数第二个数是b[j - 1]的集合,最大长度是fi - 1 + 1;输出一个整数,表示最大上升子序列和。
1≤N≤1000
7
1 7 3 5 9 4 8
18
思路 :
代码 :
#include导弹拦截
链接 :
题面 :
2<=n<=500
389 207 155 300 299 170 158 65
6
2思路 :
代码 [O(n^2)]:
#include代码 [O(nlogn)] :
#include187.弹道防御系统
链接 :
思路 :
代码 :
#include 272.最长上升公共子序列
原题链接 :
思路 :
代码 :
#include