算法综合篇专题三:二分法
"寻一颗,未萌的渺小啊,随着青翠未来,升入辽阔云霄~"
现在你有一个"升序"数组,想让你在这个数组里完成查找数字n,在这个数组内的下标,你可以怎么做?这也许是不少友子们初遇二分问题的场景。你可以使用O(N)的时间复杂度,对该数组进行遍历,就像这样。
void FindNum(vector& arr,int n)
{
for(int i=0;i 可是我们没有很好地利用到数组“有序”的特点,我们可以令数字为mid,那么借着有序的特点,可以将这个数组划分为两个区域,一边是小于mid的数,一边是大于mid的数。
void FindNum(vector& arr,int n)
{
int left = 0,right = arr.size()-1;
while(left < right)
{
int mid = (left + right) / 2;
if(arr[mid] < n) mid = left+1;
else if(arr[mid] > m ) mid = right-1;
else mid;
}
return -1;
} 所以,按照这样的算法查找数组中的某个数,时间复杂度可以下降为O(logN),是一个特别大的提升,但使用这个算法的前前提的 “数组有序”。
——前言
1、二分查找
(1) 题目解析 
这道题是最朴素的二分查找,同前言举的例子是一样的解题思路。
(2) 算法原理
class Solution {
public:
int search(vector& nums, int target) {
int left = 0,right = nums.size()-1;
// 当left==right时 当前元素是没有判断的
// 因此这里需要再循环一次
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] > target){
right = mid - 1;
}
else if(nums[mid] < target){
left = mid + 1;
}
else return mid;
}
return -1;
}
};
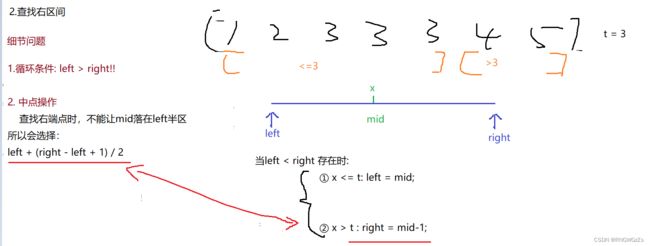
2、在排序数组中查找元素的第⼀个和最后⼀个位置
(1) 题目解析
根据数组"非递减顺序" 使用二分查找但朴素的二分查找只适用于查找一个数,所以这道题需要变形。
(2) 算法原理 
查找区间右端点也是类似过程,只是需要注意细节处理:
class Solution {
public:
vector searchRange(vector& nums, int target) {
if(nums.empty()) return {-1,-1};
int left = 0,right = nums.size()-1;
vector ret;
// 找左端点
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < target){
left = mid + 1;
}
else right = mid;
}
// 此时找到了左端点
if(nums[left] != target) ret.push_back(-1);
else ret.push_back(left);
right = nums.size()-1;
// 找右端点
while(left < right)
{
int mid = left + (right - left + 1) /2;
if(nums[mid] > target){
right = mid - 1;
}
else left = mid;
}
if(nums[right] != target) ret.push_back(-1);
else ret.push_back(right);
return ret;
}
};
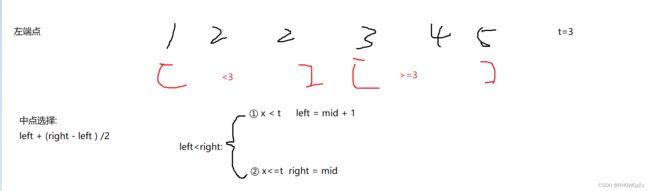
3、搜索插⼊位置
(1) 题目解析
这道题可以使用左端点和右端点解决。
(2) 算法原理
左端点:
class Solution {
public:
int searchInsert(vector& nums, int target) {
int left = 0,right = nums.size()-1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < target){
left = mid + 1;
}
else right = mid;
}
// 可能该数不存在并且 > 当前数
if(nums[left] < target) return left + 1;
return left;
}
}; 右端点:
class Solution {
public:
int searchInsert(vector& nums, int target) {
int left = 0,right = nums.size()-1;
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(nums[mid] > target){
right = mid - 1;
}
else left = mid;
}
// 可能该数不存在并且 > 当前数
if(nums[left] < target) return left + 1;
return left;
}
};
4. x 的平方根
(1) 题目解析 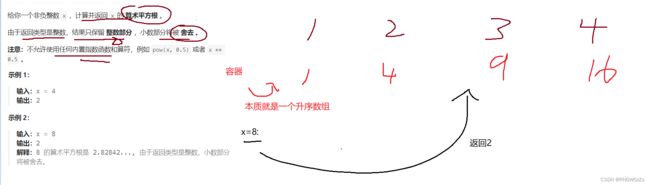
(2) 算法原理 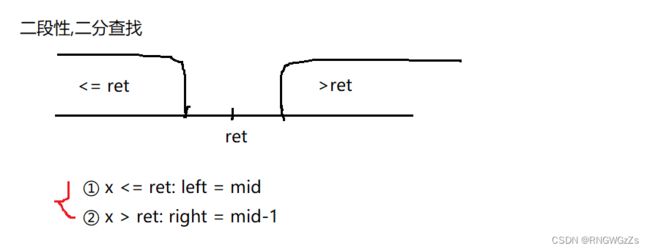
class Solution {
public:
int mySqrt(int x) {
if(x < 1) return 0;
// 1~x
int left = 1,right = x;
while(left < right)
{
int mid = left + (right -left + 1) / 2;
if(x < pow(mid,2))
{
right = mid - 1;
}
else left = mid;
}
return left;
}
};
5、山脉数组的峰顶索引
(1) 题目解析
(2) 算法原理
左端点:
class Solution {
public:
int peakIndexInMountainArray(vector& arr) {
int left = 1,right = arr.size()-2;
// [left,mid] [mid+1,right]
while(left < right)
{
int mid = left + (right - left) / 2;
// 左端点
if(arr[mid] < arr[mid+1]){
left = mid + 1;
}
else right = mid;
}
return right;
}
};
右端点:
class Solution {
public:
int peakIndexInMountainArray(vector& arr) {
int left = 1,right = arr.size()-2;
// [left,mid] [mid+1,right]
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(arr[mid] < arr[mid-1]){
right = mid - 1;
}
else left = mid;
}
return left;
}
}; 6、寻找峰值
(1) 题目解析
(2) 算法原理 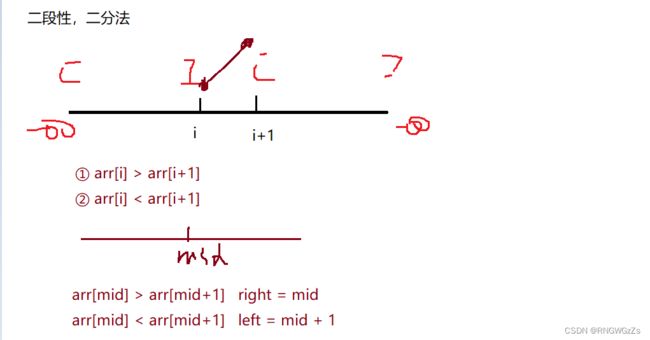
class Solution {
public:
int findPeakElement(vector& nums) {
if(nums.size() == 1) return 0;
int left = 0,right = nums.size() - 1;
while(left < right)
{
// 左端点发
int mid = left + (right - left) / 2;
if(nums[mid] < nums[mid+1]){
left = mid+1;
}
else right = mid;
}
return left;
}
};
7、寻找旋转排序数组中的最小值
(1) 题目解析
(2) 算法原理
class Solution {
public:
int findMin(vector& nums) {
int left = 0,right = nums.size()-1;
int x = nums[right]; //标记参照点
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] > x){
left = mid + 1;
}
else right = mid;
}
return nums[left];
}
};
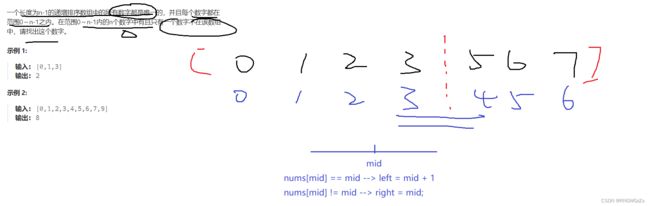
8、II. 0~n-1中缺失的数字
(1) 题目解析
(2) 算法原理
class Solution {
public:
int missingNumber(vector& nums) {
int left = 0,right = nums.size()-1;
while(left < right)
{
int mid = left + (right-left) / 2;
if(nums[mid] == mid) {
left = mid + 1;
}
else right = mid;
}
// left为0时 特殊处理
return left == nums[left] ? left+1:left;
}
}; 本篇到此结束,感谢你的阅读。
祝你好运,向阳而生~