函数式编程

函数式编程是什么

函数式编程，是“优美范式”，更是“进阶套路”。

函数式编程是一种编程范式。

编程范式可以理解为编程的风格/方式，它决定了我们将以一种什么样的方法和规范去组织自己的代码，是一门研究“如何写代码”的学问。

对前端工程师来说，我们可能接触过的编程范式有以下几种：

• 命令式编程
• 面向对象编程
• 函数式编程

我们之所以“有可能”接触过这 3 种范式，是因为 JS 是多范式的语言。

为什么选择函数式编程

为什么 React 选择逐步告别 Class 组件，拥抱“函数组件”？

为什么 Redux 的 Reducer 必须是“纯函数”？

为什么各路前端框架、小程序框架总在强调“不可变值”？

为什么各厂的前端面试中，无论是问答题目还是 coding-test，都开始越来越频繁地考察高阶函数、柯里化、偏函数、compose/pipe 等函数式能力？

归根结底，是因为函数式思想正在以越来越快的速度渗透前端生态。

在React、Redux、Ramda.js、Lodash/fp、Immutable.js、Immer.js这些现代前端框架/库中，有的借助函数式思想实现了部分功能，有的则整个基于函数式来设计自身的软件架构。

函数式编程和设计模式一样，都致力于解决软件设计的复杂度的问题，着力点都在于“如何应对变化”，引导我们用健壮的代码解决具体的问题、用抽象的思维应对复杂的系统。

前端视角看编程范式

对前端工程师来说，我们可能接触过的编程范式有以下几种：

• 命令式编程
• 面向对象编程
• 函数式编程

命令式编程关注的是一系列具体的执行步骤，当你想要使用一段命令式的代码来达到某个目的，你需要一步一步地告诉计算机应该“怎样做”。

与命令式编程严格对立的其实是“声明式编程”：不关心“怎样做”，只关心“得到什么”。

函数式编程是声明式编程的一种。

具体到范式表达上，函数式编程总是需要我们去思考这样两个问题：

• 我想要什么样的输出？
• 我应该提供什么样的输入？

一个例子：

有一个员工信息数据库。现在为了对年龄大于等于 24 岁的员工做生涯指导，需要拉出一张满足条件的员工信息清单，要求清单中每一条信息中间用逗号分隔，并按照年龄升序展示。

把这个需求简单梳理一下，分三步走：

1. 对列表进行排序
2. 筛选出 >= 24 岁这个区间内的员工列表
3. 针对该列表中的每一条员工数据历史，保存到 logText 中

命令式编程的代码如下所示：

// 这里我mock了一组员工信息作为原始数据，实际处理的数据信息量应该比这个大很多
const peopleList = [
  {
    name: 'John Lee',
    age: 24,
    career: 'engineer'
  },
  {
    name: 'Bob Chen',
    age: 22,
    career: 'engineer'
  },
  {
    name: 'Lucy Liu',
    age: 28,
    career: 'PM'
  },
  {
    name: 'Jack Zhang',
    age: 26,
    career: 'PM'
  },
  {
    name: 'Yan Xiu',
    age: 30,
    career: 'engineer'
  }
]

const len = peopleList.length

// 对员工列表按照年龄【排序】
for(let i=0;i<len;i++) {
  // 内层循环用于完成每一轮遍历过程中的重复比较+交换
  for(let j=0;j<len-1;j++) {
    // 若相邻元素前面的数比后面的大
    if(peopleList[j].age > peopleList[j+1].age) {
      // 交换两者
      [peopleList[j], peopleList[j+1]] = [peopleList[j+1], peopleList[j]]
    }
  }
}

let logText = ''
for(let i=0; i<len; i++) {
  const person = peopleList[i]
  // 【筛选】出年龄符合条件的
  if( person.age >= 24 ) {
    // 从数组中【提取】目标信息到 logText
    const perLogText = `${person.name}'s age is ${person.age}`
    if(i!==len-1) {
      logText += `${perLogText},`
    } else {
      logText += perLogText
    }
  }
}

console.log(logText)

下面再来看看函数式的解法：

// 定义筛选逻辑
const ageBiggerThan24 = (person)=> person.age >= 24

// 定义排序逻辑
const smallAgeFirst = (a, b) => {
  return a.age - b.age
}

// 定义信息提取逻辑
const generateLogText = (person)=>{
  const perLogText = `${person.name}'s age is ${person.age}`
  return perLogText
}

const logText = peopleList.filter(ageBiggerThan24)
                      .sort(smallAgeFirst)
                      .map(generateLogText)
                      .join(',')

console.log(logText)

作为用户不需要了解每个函数内部都执行了哪些语句，仅仅通过函数名就可以推断出来这个调用链做了哪些事情。

此外，声明式代码定义的 ageBiggerThan24、 sortByAge、getLogText等方法，是可以被复用的。

而命令式代码中的比大小、排序、字符串处理等逻辑，更像是“一锤子买卖”，执行完也就过去了，日后想要实现相同的逻辑，只能靠复制粘贴。

在函数式编程的代码组织模式下，我们关注的不再是具体逻辑的实现，而是对“变换”的组合。

那么就 JS 函数式编程而言，以下三个特征是其关键：

• 拥抱纯函数，隔离副作用
• 函数是“一等公民”
• 避免对状态的改变（不可变值）

纯函数与副作用

纯函数是函数式编程的一个最大的前提，也是这坨知识体系的根基。

接下来我们探讨一下以下问题：

• 纯函数、副作用的内涵
• 纯函数/非纯函数的辨析
• 从数据流的角度理解“纯”与“不纯”的本质
• 纯函数解决了什么问题

纯函数、副作用的定义

什么是纯函数？

同时满足以下两个特征的函数，我们就认为是纯函数：

• 对于相同的输入，总是会得到相同的输出
• 在执行过程中没有语义上可观察的副作用。

什么是副作用？

如果一个函数除了计算之外，还对它的执行上下文、执行宿主等外部环境造成了一些其它的影响，那么这些影响就是所谓的”副作用”。

看几个例子：

下面这个add()函数不是一个纯函数，因为它违背了对于相同的输入，总是会得到相同的输出。只要在全局作用域上改变a和b的值，那么这个函数执行后就没办法得到相同的输出。

let a = 10
let b = 20

function add() {
  return a+b
}

改为纯函数：

let a = 10  
let b = 20

function add(a, b) {
  return a+b
}

简单的改造后，add 函数就能够充分满足纯函数的两个条件了：

1. 对于相同的输入，总是会得到相同的输出：对于相同的 a 和 b 来说，它们的和总是相等的✅
2. 在执行过程中没有语义上可观察的副作用：add() 函数除了加法计算之外没有做任何事，不会对外部世界造成额外影响✅

下面这个函数也是一个不纯的函数，console.log() 会在控制台打印一行文字，这改变了浏览器的控制台，属于对外部世界的影响，也就是说 processName 函数在执行过程中产生了副作用。

function processName(firstName, secondName) {
  const fullName = `${firstName}·${secondName}`
  console.log(`I am ${fullName}`)
  return fullName
}

processName('约瑟翰', '庞麦郎')

要想把它改回纯函数也非常简单，只需要像这样把副作用摘出去就可以了：

function processName(firstName, secondName) {
  const fullName = `${firstName}·${secondName}`
  return fullName
}

console.log(processName('约瑟翰', '庞麦郎'))

再看一个网络请求函数，它也不是一个纯函数，一个引入了网络请求的函数，从原则上来说是纯不起来的。

function getData(url) {
  const response = await fetch(url)
  cosnt { data } = response   
  return data
}

为什么网络请求会使函数变得不纯呢？我们以示例代码中的 get 请求为例来分析一下：

• 请求获取到的 response 是动态的：需要通过网络请求获取的数据往往是动态的，对于相同的输入，服务端未必能够给到相同的输出。
• 请求可能出错：既然是网络请求，那就一定要考虑失败率的问题。网络拥塞、机房起火、后端删库跑路等等问题都有可能导致请求过程中的 Error，未经捕获的 Error 本身就是一种副作用。

当请求方法为 post、delete 等具有“写”能力的类型时，网络请求将会执行对外部数据的写操作，这会使函数的“不纯”更进一步。

看了这些例子，让我们来对纯函数的定义做一次总结：

纯函数：输入只能够以参数形式传入，输出只能够以返回值形式传递，除了入参和返回值之外，不以任何其它形式和外界进行数据交换的函数。

函数为何非纯不可？

纯函数解决了两个大问题，那就是“不确定性”和“副作用”。

纯函数，高度确定的函数

不纯的函数（Impure function）最直接的问题，就是不确定性

Impure function 的行为是难以预测的；对于同样的输入，Impure function 不能够保证同样的输出。

以测试过程为例：单元测试的主要判断的依据就是函数的输入和输出。

如果对于同样的输入，函数不能够给到确定的输出，测试的难度将会陡然上升。

不确定性也会导致我们的代码难以被调试、数据变化难以被追溯、计算结果难以被复用等等。

总而言之一句话：不确定性意味着风险，而风险是万恶之源。

纯函数，没有副作用的函数

消除副作用，足以解决函数中大多数的不确定性。

此外，副作用的消除还解决了并行计算带来的竞争问题。

不纯的函数有可能访问同一块资源，进而相互影响，引发意想不到的混乱结果。

而纯函数则不存在这种问题，纯函数的计算完全发生在函数的内部，它不会对外部资源产生任何影响，因此纯函数的并行计算总是安全的。

纯函数，更加灵活的函数

不纯的函数是不灵活的

它们只能在某一个特定的上下文里运行，一旦脱离了这个上下文，就会失去预期中的效用。

纯函数则完全不存在这个弊端，因为它太简单了，它除了入参谁也不认，除了计算啥也不干。

因此，纯函数是高度灵活的函数，它的计算逻辑在任何上下文里都是成立的。

纯函数，可以改善代码质量

从研发效率上来看，纯函数的实践，实际上是将程序的“外部影响”和“内部计算”解耦了。

这间接地促成了程序逻辑的分层，将会使得模块的功能更加内聚。

作为程序员在开发中，不再需要去关注函数可能会造成的外部影响，只需要关注函数本身的运算逻辑。

这和设计模式的“单一职责”原则有异曲同工之妙

设计模式中，我们强调将“变与不变”分离，而纯函数强调将计算与副作用分离。

计算是确定性的行为，而副作用则充满了不确定性。这一实践，本质上也是在贯彻“变与不变分离”的设计原则。

这样的逻辑分层将会使得我们的程序更加健壮和灵活，也会促成更加专注、高效的协作。

副作用不是毒药

对于纯函数来说，副作用无疑是地雷、是毒药。

但对于一个完整的程序来说，副作用却至关重要。

函数生产的是数据，这些数据要想作用于外部世界、创造一些真正的改变，就必须借助副作用。

试想，公司为什么要花钱雇程序员？

因为要做网页，这需要程序员操作DOM；因为要 CRUD，这需要程序员操作DB；因为要读写文件，这需要程序员执行 IO…… 如果我们试图把一个业务程序员的简历用一句话概括，那无外乎“精通实现各种副作用”。

老板和客户不会关心你的代码是否优雅，只会关心那些肉眼可见的副作用——页面渲染、网络请求、数据读写等等是否符合预期。

对于程序员来说，实践纯函数的目的并不是消灭副作用，而是将计算逻辑与副作用做合理的分层解耦，从而提升我们的编码质量和执行效率。

纯函数的这些规则并不是为了约束而约束，而是为了追求更高的确定性；

同时引导我们做更加合理的逻辑分层，写出更加清晰、更善于应对变化的代码。

函数是一等公民

如果一门编程语言将函数当做一等公民对待，那么这门语言被称作“拥有头等函数”

当一门编程语言的函数可以被当作变量一样用时，则称这门语言拥有头等函数。例如，在这门语言中，函数可以被当作参数传递给其他函数，可以作为另一个函数的返回值，还可以被赋值给一个变量。 ——MDN Web Docs

【划重点】：头等函数的核心特征是“可以被当做变量一样用”。

“可以被当做变量一样用”意味着什么？它意味着：

1. 可以被当作参数传递给其他函数
2. 可以作为另一个函数的返回值
3. 可以被赋值给一个变量

以上三条，就是“函数是一等公民”这句话的内涵。

“一等公民”的 JS 函数

看几个例子：

JS 函数可以被赋值给一个变量

// 将一个匿名函数赋值给变量 callMe
let callMe = () => {
   console.log('Hello World！')
}

// 输出 callMe 的内容
console.log(callMe)

// 调用 callMe
callMe()

JS 函数可以作为参数传递

咱要是说“JS 函数作为参数传递”，你可能还不太能转过这个弯儿来。

但咱要是说“回调函数”，你肯定一下就来精神了——它可不就是在说回调函数么！

众所周知，回调函数是 JS 异步编程的基础。

在前端，我们常用的事件监听、发布订阅等操作都需要借助回调函数来实现。比如这样：

function consoleTrigger() {
    console.log('spEvent 被触发')
}   

jQuery.subscribe('spEvent', consoleTrigger)

在这个例子中，consoleTrigger 函数就作为 subscribe 函数的第 2 个入参被传递。

而在 Node 层，我们更是需要回调函数来帮我们完成与外部世界的一系列交互（也就是所谓的“副作用”）。

这里举一个异步读取文件的例子：

function showData(err, data){
    if(err) {
      throw err
    }
    // 输出文件内容
    console.log(data);
})

// -- 异步读取文件
fs.readFile(filePath, 'utf8', showData)

在这个例子中， showData 函数作为 readFile 函数的第 3 个入参被传递。

JS 函数可以作为另一个函数的返回值

函数作为返回值传递，基本上都是馋人家闭包的特性。比如下面这个例子：

function baseAdd(a) {
  return (b) => {
    return a + b
  };
};

const addWithOne = baseAdd(1)

// .... (也许在许多行业务逻辑执行完毕后）

const result = addWithOne(2)

显然，add 函数想要做一个加法，但是在只能够确认其中一个加数（a）的时候，它并不急于立刻做这个加法。

怎么办呢？先把这个已经确定的加数（a）以【闭包中的自由变量】的形式存起来，然后返回一个待执行的加法函数。等什么时候第二个加数也确定了，就可以立刻执行这段逻辑。

“一等公民”的本质：JS 函数是可执行的对象

为什么 JS 中的函数这么牛x，可以为所欲为呢？本质上是因为它不仅仅是个函数，它还是个对象。

对象能干啥？咱对照“一等公民”的特征来一个一个看一下：

1. 能不能赋值给变量？能！
2. 能不能作为函数参数传递？能！
3. 能不能作为返回值返回？能！

到这里我们不难看出，“First-Class Function（头等函数）” 的本质，其实是"First-Class Object（头等对象）”。

JS 函数的本质，就是可执行的对象。

JS 世界的“不可变数据”

JS中的数据类型，整体上来说只有两类：值类型（也称基本类型/原始值）和引用类型（也称复杂类型/引用值）。

其中值类型包括：String、Number、Boolean、null、undefined、Symbol

这类型的数据最明显的特征是大小固定、体积轻量、相对简单。

而排除掉值类型，剩下的 Object 类型就是引用类型（复杂类型）

这类数据相对复杂、占用空间较大、且大小不定。

保存值类型的变量是按值访问的， 保存引用类型的变量是按引用访问的。

这两类数据之间最大的区别，在于变量保存了数据之后，我们还能对这个数据做什么。

不可变的值，可变的引用内容

值类型的数据无法被修改，当我们修改值类型变量的时候，本质上会创建一个新的值。

let a = 1
let b = a

// true
a === b

b = 2

// false
a === b

当我把 a 赋值给 b 的时候，相当于在内存里开辟了一个新的坑位，然后将此时此刻的 a 值拷贝了一份、塞了进去。从这一刻开始，a 和 b 各据一坑，界限分明，谁也不会再影响谁。

当修改 b 值的时候，相当于解除了 b 变量和旧的 b 值（也就是 1）之间的关联关系，然后建立了 b 变量和新的 b 值（也就是 2）之间的关联关系。此时 b 的值已经发生了变化，但 a 坑里的 1 纹丝不动。

在这整个过程中，出现的值有三个：a 值 = 1、b 值（初始值） = 1、b 值（修改后） = 2。

1、1、2 这三个数字从创建开始就不会再发生任何改变

我们修改 b 值的时候，其实是在修改数字 1、2 与“b 变量”之间的关系，而并不是在修改数字本身。

像数字类型这样，自创建起就无法再被修改的数据，我们称其为“不可变数据”。

对应到 JS 的数据分类上，“值类型”数据均为不可变数据。

但引用类型就没有那么好对付了。在引用本身不变的情况下，引用所指向的内容是可以发生改变的。

const a = {
  name: 'ruimengmeng',
  age: 30
}

const b = a


// true 
a === b 

b.name = 'mengmengda'   
 
// true
a === b 

对于引用类型来说，当把 a 对象赋值给 b 时，并不会发生“开辟一个新的 b 对象坑位、放入一份 a 对象的副本”这种事——JS 会直接把 a 的引用赋值给 b。

引用类型的赋值过程本质上是给同一块数据内容起一个新的名字。赋值结束后，a 和 b 都会指向内存中的同一块数据。

对于引用类型来说，我们总是可以在数据被创建后，随时修改数据的内容。

像这种创建后仍然可以被修改的数据，我们称其为“可变数据”。

为什么函数式编程不喜欢可变数据

可变数据使函数行为变得难以预测

可变数据带来的最根本的问题——不确定性。

可变数据会使数据的变化变得隐蔽，进而使函数的行为变得难以预测。

在函数式编程这种范式下，我们校验一个函数有效性的关键依据，永远是“针对已知的输入，能否给出符合预期的输出”，这样的校验非常清晰、且容易实现。

而可变数据的出现则将会使函数的作用边界变得模糊，进而导致使用者、甚至开发者自身都难以预测它的行为最终会指向什么样的结果。同时，这也会大大增加测试的难度。

可变数据使函数复用成本变高

可变数据的存在，要求我们不得不在调用一个函数之前，先去了解它的逻辑细节、定位它对外部数据的依赖情况和影响情况，由此来确保调用动作的安全性。

而当我们使用某一个函数的时候，我们会默认它是一个黑盒

我们关注的都是这个函数的效用、函数的输入与输出，而不会去关注它的实现细节。

因此，我们有必要确保，这个黑盒是可靠的、受控的。

一个可靠、受控的黑盒，应该总是将变化控制在盒子的内部，而不去改变盒子外面的任何东西。

要想做到这一点，就必须把可变数据从我们的函数代码里铲除干净。

“不可变”不是要消灭变化，而是要控制变化

大家知道，我们现代前端应用的复杂度整体是比较高的，其中最引入注目的莫过于“状态的复杂度”。

“状态”其实就是数据。

一个看似简单的页面，背后可能就有几十上百个状态需要维护

如果没有状态之间的相互作用、相互转化，又怎能将精彩纷呈的前端交互呈现给用户呢？

程序失去变化，宛如人类失去灵魂。

所以说，消灭变化是不可能的事情，也是万万不可的事情。

我们真正要做的，是控制变化，确保所有的变化都在可预期的范围内发生，从而防止我们的程序被变化“偷袭”。

不可变数据の实践原则：拷贝，而不是修改

先看一个修改的例子：

function dynamicCreateJob(baseJob) {
  let newJob = baseJob
  if(isHighPosition()) {
      newJob.level = 10 
  }
  return newJob
}

这个粗糙版本显然并没有遵循“不可变数据”的原则——它直接在 baseJob 的对象本体上进行了篡改。

再看一个最常用的拷贝方式：

function dynamicCreateJob(baseJob) {
  // 创建一个 baseJob 的副本
  let newJob = {...baseJob}
  if(isHighPosition()) {
      newJob.level = 10 
  }
  return newJob
}

通过拷贝，我们顺利地将变化控制在了 dynamicCreateJob() 函数内部，避免了对全局其它逻辑模块的影响。

用拷贝代替修改后，baseJob 对于 dynamicCreateJob() 函数来说，成为了一个彻头彻尾的只读数据。

对于函数式编程来说，函数的外部数据是只读的，函数的内部数据则是可写的。

对于一个纯函数来说，它需要把自己的入参当做只读数据，它也需要把自己可访问的所有全局变量/自由变量当做只读数据。 有且仅有这些外部数据，存在【只读】的必要。

不可变数据的两种最直接的实践思路：

对于值类型数据，可以使用 const 来确保其不变性；

对于引用类型数据，可以使用拷贝来确保源数据的不变性。

这其中，引用类型数据的不可变性值得我们再三思考——有没有比拷贝更加高效的解法呢？

答案当然是有啦，接下来我们就学习一下不可变数据的进阶解法中最有名的一个——持久化数据结构

持久化数据结构

通过上面的学习我们已经知道，用拷贝代替修改，是确保引用类型数据不可变性的一剂良药。

然而，拷贝并非一个万能的解法。拷贝意味着重复，而重复往往伴随着着冗余。

当数据规模大、数据拷贝行为频繁时，拷贝将会给我们的应用性能带来巨大的挑战。

拷贝出来的冗余数据将盘踞大量的内存，挤占其它任务的生存空间；

此外，拷贝行为本身也是需要吃 CPU 的，持续而频繁的拷贝动作，无疑将拖慢应用程序的反应速度。

因此，对于状态简单、逻辑轻量的应用来说，拷贝确实是一剂维持数据不可变性的良药。

但是对于数据规模巨大、数据变化频繁的应用来说，拷贝意味着一场性能灾难。

接下来就来学习一下什么是持久化数据结构。

先看两个持久化数据结构实际使用的例子：

Immutable.js

React 开发者对它应该不会感到陌生。 Immutable.js 是持久化数据结构在前端领域影响最深远的一次实践。

// 引入 immutable 库里的 Map 对象，它用于创建对象
import { Map } from 'immutable'

// 初始化一个对象 baseMap
const originData = Map({
  name: 'ruimengmeng',
  hobby: 'coding',
  age: 777
})

// 使用 immutable 暴露的 Api 来修改 baseMap 的内容
const mutatedData = originData.set({
  age: 77.7
})

// 我们会发现修改 baseMap 后将会返回一个新的对象，这个对象的引用和 baseMap 是不同的
console.log('originData === mutatedData', originData === mutatedData)

Immutable.js 提供了一系列的 Api，这些 Api 将帮助我们确保数据的不可变性。

从代码上来看，它省掉了我们手动拷贝的麻烦。

从效率上来说，它在底层应用了持久化数据结构，解决了暴力拷贝带来的各种问题。

Git commit

在创建 commit 时，git 会对整个项目的所有文件做一个“快照”。

“快照”并不是对当前所有文件的一次拷贝而已，“快照”记录的不是文件的内容，而是文件的索引。

当 commit 发生时， git 会保存当前版本所有文件的索引。

对于那些没有发生变化的文件，git 保存他们原有的索引；

对于那些已经发生变化的文件，git 会保存变化后的文件的索引。

也就是说，git 记录“变更”的粒度是文件级别的。

它会同时保有新老两份文件，不同的 version，索引指向不同的文件。

数据共享

和 git “快照”一样，持久化数据结构的精髓在于“数据共享”。

数据共享意味着将“变与不变”分离，确保只有变化的部分被处理，而不变的部分则将继续留在原地、被新的数据结构所复用。

不同的是，在 git 世界里，这个“变与不变”的区分是文件级别的；

而在 Immutable.js 的世界里，这个“变与不变”可以细化到数组的某一个元素、对象的某一个字段。

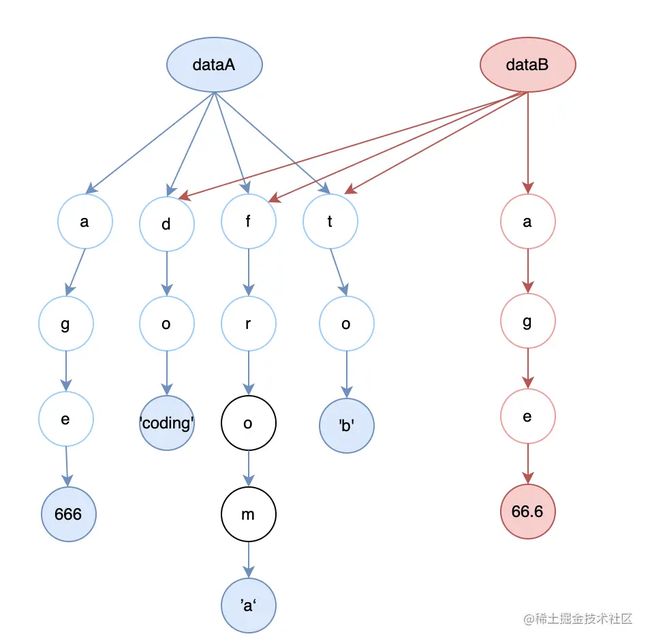
举个例子：

假如借助 Immutable.js 基于 A 对象创建出了 B 对象。

A 对象有 4 个字段：

const dataA = Map({
  do: 'coding',
  age: 666,
  from: 'a',
  to: 'b'
})

B 对象在 A 对象的基础上修改了其中的某一个字段(age)：

// 使用 immutable 暴露的 Api 来修改 baseMap 的内容
const dataB = dataA.set({
  age: 66.6
})

那么 Immutable.js 仅仅会创建变化的那部分（也就是创建一个新的 age 给 B)，并且为 B 对象生成一套指回 A 对象的指针，从而复用 A 对象中不变的那 3 个字段。

为了达到“数据共享”，持久化数据结构在底层依赖了一种经典的基础数据结构，那就是 Trie(字典树）。

当我们创建对象 B 的时候，我们可以只针对发生变化的 age 字段创建一条新的数据，并将对象 B 剩余的指针指回 A 去

Immer.js

“数据不可变性如何在前端业务中落地？”

这道题目的答案多年来几乎是“固定”的——Immutable.js/持久化数据结构

Immutable.js/持久化数据结构真的是唯一的答案吗？

Immutable.js 对于前端函数式编程来说，有划时代的意义，但它终究也只是实现 Immutability 的一种途径。

在活跃的函数式社区中，优秀的 Immutability 实践还有很多——比如，Immer.js

用 Immer.js 写代码，不需要操心深拷贝浅拷贝的事儿，更不需要背诵记忆 Immutable.js 定义的一大堆 API

所需要做的仅仅是在项目里轻轻地 Import 一个 produce：

import produce from "immer"

// 这是数据
const baseState = [
    {
        name: "aaa",
        age: 99
    },
    {
        name: "bbb",
        age: 100
    }
]

// 定义数据的写逻辑
const recipe = draft => {
    draft.push({name: "ccc", age: 101})
    draft[1].age = 102
}

// 借助 produce，执行数据的写逻辑
const nextState = produce(baseState, recipe)

这个 API 里有几个要素：

• (base)state：源数据，是我们想要修改的目标数据
• recipe：一个函数，我们可以在其中描述数据的写逻辑
• draft：recipe 函数的默认入参，它是对源数据的代理，我们可以把想要应用在源数据的变更应用在 draft 上
• produce：入口函数，它负责把上述要素串起来。

Immer.js 是如何工作的

Immer.js 实现 Immutability 的姿势非常有趣——它使用 Proxy，对目标对象的行为进行“元编程”。

Proxy 对象用于创建一个对象的代理，从而实现基本操作的拦截和自定义（如属性查找、赋值、枚举、函数调用等）。 ——MDN

Proxy 是 JS 语言中少有的“元编程”工具。所谓“元编程”，指的是对编程语言进行再定义。

借助 ES6 暴露给我们的 Proxy 构造函数，我们可以创建一个 Proxy 实例，并借助这个实例对目标对象的一些行为进行再定义。举个例子：

// 定义一个 programmer 对象
const programmer = {
  name: 'aaa',
  age: 30
}

// 定义这个对象的拦截逻辑
const proxyHandler = {
  // obj 是目标对象， key 是被访问的键名
  get(obj, key) {
    if(key === 'age')
      return 100
    return obj[key]
  }
}

// 借助 Proxy，将这个对象使用拦截逻辑包起来
const wrappedProgrammer = new Proxy(programmer, proxyHandler)

// 'aaa'
console.log(wrappedProgrammer.name)
// 100
console.log(wrappedProgrammer.age)

如这段代码所示， Proxy 接收两个参数，第一个参数是你需要处理的目标对象，第二个参数同样是一个对象，在这个对象里，描述了你希望对目标对象应用的拦截/代理行为。

在这个例子里，我借助 proxyHandler 拦截了目标对象（programmer）的 getter 方法，代理了 programmer 对象的访问行为。

每次访问 wrappedProgrammer 时，JS 不会执行 programmer 对象的默认行为（返回 obj[key]），而是会执行 proxyHandler.get() 方法所定义的行为：若访问的 key 是 age，则固定返回 100，否则返回 obj[key]。

（同理，我们也可以对目标对象的 setter 方法进行拦截，此处不再赘述）。

借助 Proxy，我们可以给目标对象创建一个代理（拦截）层、拦截原生对象的某些默认行为，进而实现对目标行为的自定义。那么 Proxy 是如何帮助 Immer.js 实现 Immutability 的呢？

Produce 关键逻辑抽象

Immer.js 的一切奥秘都蕴含在 produce 里，包括其对 Proxy 的运用。那么 produce 是如何工作的呢？

Immer.js 的源代码虽然简洁，但整个读完也是个力气活。这里我们只关注 produce 函数的核心逻辑，将其提取为如下的极简版本：

function produce(base, recipe) {
  // 预定义一个 copy 副本
  let copy
  // 定义 base 对象的 proxy handler
  const baseHandler = {
    set(obj, key, value) {
      // 先检查 copy 是否存在，如果不存在，创建 copy
      if (!copy) {
        copy = { ...base }
      }
      // 如果 copy 存在，修改 copy，而不是 base
      copy[key] = value
      return true
    }
  }
  // 被 proxy 包装后的 base 记为 draft
  const draft = new Proxy(base, baseHandler)
  // 将 draft 作为入参传入 recipe
  recipe(draft)
  // 返回一个被“冻结”的 copy，如果 copy 不存在，表示没有执行写操作，返回 base 即可
  // “冻结”是为了避免意外的修改发生，进一步保证数据的纯度
  return Object.freeze(copy || base)
}

接下来我尝试对这个超简易版的 producer 进行一系列的调用（解析在注释里）：

// 这是我的源对象
const baseObj = {
  a: 1,
  b: {
    name: "修言"
  }
}

// 这是一个执行写操作的 recipe
const changeA = (draft) => {
  draft.a = 2
}

// 这是一个不执行写操作、只执行读操作的 recipe
const doNothing = (draft) => {
  console.log("doNothing function is called, and draft is", draft)
}

// 借助 produce，对源对象应用写操作，修改源对象里的 a 属性
const changedObjA = produce(baseObj, changeA)

// 借助 produce，对源对象应用读操作
const doNothingObj = produce(baseObj, doNothing)

// 顺序输出3个对象，确认写操作确实生效了
console.log(baseObj)      // {a: 1,b: {name: "修言"}}
console.log(changedObjA)  // {a: 2,b: {name: "修言"}}
console.log(doNothingObj) // {a: 1,b: {name: "修言"}}

// 【源对象】 和 【借助 produce 对源对象执行过读操作后的对象】 还是同一个对象吗？
// 答案为 true
console.log(baseObj === doNothingObj)
// 【源对象】 和 【借助 produce 对源对象执行过写操作后的对象】 还是同一个对象吗？
// 答案为 false
console.log(baseObj === changedObjA)
// 源对象里没有被执行写操作的 b 属性，在 produce 执行前后是否会发生变化？
// 输出为 true，说明不会发生变化
console.log(baseObj.b === changedObjA.b)

貌似上面这个produce实现起来每次还是需要浅拷贝啊？别急，让我们来看看produce的原理

Produce 原理：将拷贝操作精准化

将“变与不变”分离，确保只有变化的部分被处理，而不变的部分则将继续留在原地。

不难看出，produce 可以像 Immutable.js 一样，精准打击那些需要执行写操作的数据。

但 produce 并没有像 Immutable.js 一样打数据结构的主意，而是将火力集中对准了“拷贝”这个动作。

它严格地控制了“拷贝”发生的时机：

当且仅当写操作确实发生时，拷贝动作才会被执行。只要写操作没执行，拷贝动作就不会发生。

只有当写操作确实执行，也就是当我们试图修改 baseObj 的 a 属性时，produce 才会去执行拷贝动作：

先浅拷贝一个 baseObj 的副本对象（changedObjA）出来，然后再修改 changedObjA 里的 a。

这样一来，changedObjA 和 baseObj 显然是两个不同的对象，数据内容的变化和引用的变化同步发生了，这符合我们对 Immutability 的预期。

与此同时，changedObjA.b 和 baseObj.b 是严格相等的，说明两个引用不同的对象，仍然共享着那些没有实际被修改到的数据。由此也就实现了数据共享，避免了暴力拷贝带来的各种问题。

produce 借助 Proxy，将拷贝动作发生的时机和 setter 函数的触发时机牢牢绑定，确保了拷贝动作的精确性。

那万一是一个嵌套对象怎么办呢？

Produce 逐层拷贝

在上面的极简版 produce 里，着重突出了 setter 函数的写逻辑，也就是对“拷贝时机”的描述，淡化了其它执行层面的细节。而在 Immer.js 中，完整版 produce 的浅拷贝其实是可递归的。

无论对象嵌套了多少层，每一层对于写操作的反应是一致的，都会表现为“修改时拷贝”。

这是因为 produce 不仅会拦截 setter ，也会拦截 getter。

通过对 getter 的拦截，produce 能够按需地对被访问到的属性进行“懒代理”：你访问得有多深，代理逻辑就能走多深；而所有被代理的属性，都会具备新的 setter 方法。

当写操作发生时，setter 方法就会被逐层触发，呈现“逐层浅拷贝”的效果。

“逐层浅拷贝”是 Immer 实现数据共享的关键。

假设我的对象嵌套层级为 10 层，而我对它的属性修改只会触达第 2 层，“逐层的浅拷贝”就能够帮我们确保拷贝只会进行到第 2 层。“逐层的浅拷贝”如果递归到最后一层，就会变成深拷贝。

对于引用类型数据来说，“暴力拷贝”指的也就是深拷贝。

“暴力拷贝”之所以会带来大量的时间空间上的浪费，本质上是因为它在拷贝的过程中不能够“知其所止”。

而“逐层的浅拷贝”之所以能够实现数据共享，正是因为它借助 Proxy 做到了“知其所止”。

按需变化

无论是“精准拷贝”、“修改时拷贝”，还是“逐层拷贝”，其背后体现的都是同一个思想——“按需”。

对于 Immutable.js 来说，它通过构建一套原生 JS 无法支持的 Trie 数据结构，最终实现了树节点的按需创建。

对于 Immer.js 来说，它借助 Proxy 的 getter 函数实现了按需代理，借助 Proxy 的 setter 函数实现了对象属性的按需拷贝。

Immutable.js 底层是持久化数据结构，而 Immer.js 的底层是 Proxy 代理模式。

两者虽然在具体的工作原理上大相径庭，但最终指向的目的却是一致的：

使数据的引用与数据内容的变化同步发生；并且在过程中按需处理具体的变化点，提升不可变数据的执行效率。

可见，想要实现高效的 Immutability，“按需变化”是一个不错的切入点。

因为DRY，所以HOF

什么是DRY？

DRY 是一个缩写，全拼是 Don’t Repeat Yourself。

直译过来，就是“不要重复你自己”

这是一个重要的设计原则，也是程序员的基本行事准则。

具体到编码上来，就是提醒我们，不要做重复的工作，不要把同一段代码写N次。

当我们多次遇到同一个问题，多次用到重复的解法时，我们就应该把重复的这部分提取出来，而不是 ctrl-c + ctrl-v 四处复制粘贴。

DRY 原则的 JS 实践：HOF

实践 DRY 原则最重要的一点，就是将“变与不变”分离。

这时不妨回顾一下，什么是函数？函数就是下面这个东西：

y = f(x)

出参 y 是因变量，函数体 f 是计算逻辑，函数入参 x 就是自变量。

函数体一旦被定义了就无法再修改，所以，我们使用函数体来承接“不变”。

因变量和自变量都是动态可变的，但因变量变化的前提是自变量的变化。

自变量确定的情况下，因变量也是不变的。

因此，唯一可以用来承接“变”的要素，只有自变量。也就是函数的入参。

我们要想办法把变化的算式，作为一个入参传递给 arrCompute()。

在一些语言中，你或许可以直接把一坨计算逻辑作为入参传递给函数。但在 JS 的世界里，这是行不通的，要想把逻辑作为入参传递，我们必须把它包装成函数。

本着“不变”构造成通用函数体，“变”包装成函数作为入参传递的原则，我们来看一个例子：

题目——使用原生 JS，实现如下三个函数：

1. 迭代做加法：函数入参为一个数字数组，对数组中每个元素做 +1 操作，并把计算结果输出到一个新数组 newArr。
   fe：输入 [1,2,3]，输出 [2,3,4]
2. 迭代做乘法：函数入参为一个数字数组，对数组中每个元素做 *3 操作，并把计算结果输出到一个新数组 newArr。
   fe：输入 [1,2,3]，输出 [3,6,9]
3. 迭代做除法：函数入参为一个数字数组，对数组中每个元素做 /2 操作，并把计算结果输出到一个新数组 newArr。
   fe：输入 [2,4,6]，输出 [1,2,3]

大家最原始的做法肯定是分别写三个做运算的函数来完成任务：

// 迭代做加法
function arrAdd1(arr) {
  const newArr = []  
  for(let i=0; i<arr.length; i++) {
    newArr.push(arr[i]+1)
  }
  return newArr
}  

// 迭代做乘法 
function arrMult3(arr) {
  const newArr = []  
  for(let i=0; i<arr.length; i++) {
    newArr.push(arr[i]*3)
  }
  return newArr
} 

// 迭代做除法
function arrDivide2(arr) {
  const newArr = []  
  for(let i=0; i<arr.length; i++) {
    newArr.push(arr[i]/2)
  }
  return newArr
} 

// 输出 [2, 3, 4]
console.log(arrAdd1([1,2,3]))   
// 输出 [3, 6, 9]
console.log(arrMult3([1,2,3])) 
// 输出 [1, 2, 3]
console.log(arrDivide2([2,4,6]))  

我们可以看到，这三个函数的输出都是符合预期的，代码逻辑也没有毛病。但是问题就出在代码的设计上，这段代码并没有遵循 DRY 原则。我们再来看一下改造之后的代码：

// +1 函数 
function add1(num) {
  return num + 1  
}  

// *3函数
function mult3(num) {
  return num * 3 
}  

// /2函数
function divide2(num) {
  return num / 2
}

function arrCompute(arr, compute) {
  const newArr = []  
  for(let i=0; i<arr.length; i++) {
    // 变化的算式以函数的形式传入
    newArr.push(compute(arr[i]))
  }
  return newArr
}

// 输出 [2, 3, 4]
console.log(arrCompute([1,2,3], add1))
// 输出 [3, 6, 9]
console.log(arrCompute([1,2,3], mult3)) 
// 输出 [1, 2, 3]
console.log(arrCompute([2,4,6], divide2))  

我们把不变的逻辑提取为一个通用的函数，而变化的部分作为函数的入参传入。

其中的 arrCompute() 函数，就是一个高阶函数（HOF）。

高阶函数，指的就是接收函数作为入参，或者将函数作为出参返回的函数。

WHY HOF？

既然实现的都是同样的功能，为什么我们程序员一定要 DRY、为什么用高阶函数来做就比复制粘贴梭哈更好呢？

更简洁的代码，方便读写

对比上面数组计算这几个函数，改造后的代码，给人最直接的感受，就是比改造前的代码要简洁许多。

这个 case 里我们提取的公共逻辑不算很复杂，实际上越复杂的公共逻辑，提取前后的代码行数对比越明显。

通过抽取重复的逻辑到高阶函数里，我们可以减少大量复制粘贴带来的冗余代码。

更少的代码，意味着更小的编码负担，更好的可读性。

代码可复用，利人利己

用高阶函数，最直接的目的就是为了能够复用代码，减少重复，避免复制粘贴。

对于开发者本人来说， 自己写的代码，自己自然是熟悉的，复制粘贴顶多算是一个体力活。

但如果明天同时想写一个类似的功能，就不得不自己重新实现一遍别人写过的逻辑。

实践 DRY 原则，不仅仅是为了方便自己的工作，也是为了提升整个团队的研发效率。

清晰的逻辑边界，更少的测试工作

谁能保证复制粘贴的过程，不会出错呢？

万一在复制粘贴的时候，在某个业务函数里少贴了一行，干扰了业务层面的输出，这不是寄了嘛。

这些都是很有可能的，因为我们是人，人远没有计算机可靠。

因为不可靠的人类无法保证每一个函数的质量，测试就不得不对涉及到的多个函数做全面的回归测试。

但实际上，业务函数本身是不变的，我们可能仅仅是在原有的基础上做一个小计算而已。

也就是说，如果我们研发能够提前把变与不变通过函数的形式划分清楚，那么测试根本不需要做那么多重复的工

作，他只需要对增量部分的函数做测试就可以了。

Reduce：函数式语言的“万金油”

没错，我说的就是数组方法，包括但不限于 map()、reduce()、filter() 等等等等…

其中，最特别的一个是 reduce()。

几乎任何在范式上支持了函数式编程的语言，都原生支持了 reduce()。

在 JS 中，基于 reduce()，我们不仅能够推导出其它数组方法，更能够推导出经典的函数组合过程。

Reduce 工作流分析

接下来我们先通过一个小快速分析一波 reduce 的工作流特征。

const arr = [1, 2, 3]

// 0 + 1 + 2 + 3 
const initialValue = 0  
const add = (previousValue, currentValue) => previousValue + currentValue
const sumArr = arr.reduce(
  add,
  initialValue
)

console.log(sumArr)
// expected output: 6

众所周知，reduce()是一个高阶函数，它的第一个入参是回调函数，第二个入参是初始值。

Array.prototype.reduce()调用发生后，它会逐步将数组中的每个元素作为回调函数的入参传入，并且将每一步的计算结果汇总到最终的单个返回值里去。

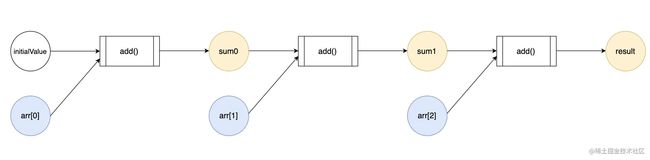
以楼上的 case 为例，它的工作流是这样的：

1. 执行回调函数 add()，入参为(initialValue, arr[0])。这一步的计算结果为记为 sum0，sum0=intialValue + arr[0]，此时剩余待遍历的数组内容为[2, 3]，待遍历元素2个。
2. 执行回调函数 add()，入参为 (sum0, arr[1])。这一步的计算结果记为 sum1，sum1 = sum0 + arr[1]，此时剩余待遍历的数组内容为 [3] ，待遍历元素1个。
3. 执行回调函数 add()，入参为 (sum1, arr[2])，这一步的计算结果记为 sum2，sum2 = sum1 + arr[2]，此时数组中剩余待遍历的元素是 []，遍历结束。
4. 输出 sum2 作为 reduce() 的执行结果， sum2 是一个单一的值。

这个过程本质上是一个循环调用add()函数的过程，上一次 add()函数调用的输出，会成为下一次 add()函数调用的输入。

用 reduce() 推导 map()

先看map()，众所周知 map() 长这样，它看上去和 reduce()没有一毛钱关系：

const arr = [1,2,3]  

const add1 = (num)=> num+1
// newArr: [2, 3, 4]
const newArr = arr.map(add1)    

arr === newArr  // false

对比 newArr 和 arr，我们可以看到它们之间的不等关系。

这说明 newArr 是一个新创建出来的数组——map() 方法不会改变原有的 arr 数组，而是会把结果放在一个新创建出来的数组里返回，这符合我们对不可变数据的预期。

map() 方法创建一个新数组，这个新数组由原数组中的每个元素都调用一次提供的函数后的返回值组成。 —— MDN

就这个例子来说，map() 遍历了 arr 数组中的每一个元素，给每一个元素执行一遍 add1() 这个 callback 后，把执行结果放在一个新的数组里返回。把这个过程用代码表达出来，看上去会更清晰：

const map = (arr, callback) => {
  const len = arr.length  
  // 创建一个新数组用来承接计算结果
  const newArr = []
  // 遍历原有数组中的每一个元素
  for(let i=0; i<len; i++) {  
    // 逐个对每个元素做 callback 计算，
    newArr.push(callback(arr[i]))
  }
  return newArr
}

在 add1() 这个 case 里，整个map() 的计算过程共有以下要素参加：

1. arr 数组里的所有数字。
2. newArr，它最初是一个空数组 []，在循环体中被反复 push()。

我们把每次循环列出来看：

1. 初始化状态，newArr = []，剩余待遍历的数组内容为 [1,2,3]，待遍历元素3个。
2. 计算 callback(arr[0])，把计算结果推入 newArr。此时 newArr = [2]，剩余待遍历的数组内容为 [2, 3]，待遍历元素2个。
3. 计算 callback(arr[1])，把计算结果推入 newArr。此时 newArr= [2, 3]，剩余待遍历的数组内容为 [3] ，待遍历元素1个。
4. 计算 callback[arr[2]]，把计算结果推入 newArr，此时 newArr= [2, 3, 4]，剩余待遍历的数组内容为 []，待遍历元素0个。
5. 输出 newArr 作为 map() 的执行结果， newArr 是一个单一的值（一个单一的数组）。

大家细品一下这个过程，是不是开始隐约觉得它和楼上的 reduce()好像有点神似——它们都吃进【多个】入参、吐出【一个】出参。

不同点仅仅在于出参的类型：reduce 编码示例中的出参是一个数字 6，而 map 编码示例中的出参是一个数组[2, 3, 4]。但出参类型的不同，其实是由 callback 的不同导致的，而不是由流程上的差异导致的。

有没有可能，我微调一下 reduce()的 callback，它的输出就和 map()一致了呢？

具体来说，我们可以把 map() 编码示例中的 add1()回调逻辑和 newArr.push() 这个动作看做是同一坨逻辑，给它起名叫 add1AndPush()。

function add1AndPush(previousValue, currentValue) {
  // previousValue 是一个数组
  previousValue.push(currentValue + 1)
  return previousValue
}

然后我用 reduce() 去调用这个 add1AndPush()：

const arr = [1,2,3]
const newArray = arr.reduce(add1AndPush, [])

你会发现，这段代码的工作内容和楼上我们刚分析过的 map() 是等价的。

破案了，map() 的过程本质上也是一个 reduce()的过程！

区别仅仅在于， reduce() 本体的回调函数入参可以是任何值，出参也可以是任何值；

而 map 则是一个相对特殊的 reduce() ，它锁定了一个数组作为每次回调的第一个入参，并且限定了 reduce() 的返回结果只能是数组。

通过楼上一系列的工作流拆解+逻辑分析，我们至少可以确定，map() 过程可以看作是 reduce() 过程的一种特殊的应用。

但是，reduce()真正的威力，在于它对函数组合思想的映射。

reduce() 映射了函数组合思想

通过上面例子的reduce()工作流，我们可以发现这样两个特征：

• reduce() 的回调函数在做参数组合
• reduce() 过程构建了一个函数 pipeline

reduce() 的回调函数在做参数组合

首先就 reduce() 过程中的单个步骤来说，每一次回调执行，都会吃进 2 个参数，吐出 1 个结果。

我们可以把每一次的调用看做是把 2 个入参被【组合】进了 callback 函数里，最后转化出 1 个出参的过程。

我们把数组中的 n 个元素看做 n 个参数，那么 reduce() 的过程，就是一个把 n 个参数逐步【组合】到一起，最终吐出 1 个结果的过程。

reduce，动词，意为减少。这个【减少】可以理解为是参数个数的减少。

reduce() 过程构建了一个函数 pipeline

reduce() 函数发起的工作流，可以看作是一个函数 pipeline。

尽管每次调用的都是同一个函数，但上一个函数的输出，总是会成为下一个函数的输入。

同时，reduce() pipeline 里的每一个任务都是一样的，仅仅是入参不同，这极大地约束了 pipeline 的能力。

这、这是不是有点浪费？有没有可能把 pipeline 里的每一个函数也弄成不一样的呢？

答案是肯定的——可能，可太能了！

reduce() 之所以能够作为函数式编程的“万金油”存在，本质上就是因为它映射了函数组合的思想。

而函数组合，恰恰是函数式编程中最特别、最关键的实践方法，是核心中的核心，堪称“核中核”。

那么函数组合到底是什么？它在实践中的形态是什么样的？又该如何借助reduce()来实现函数组合呢？

在展开讨论这些问题之前，我们首先得整明白“声明式的数据流”是啥。

声明式数据流

考虑这样一个数字数组 arr：

const arr = [1, 2, 3, 4, 5, 6, 7, 8]  

现在我想以 arr 数组作为数据源，按照如下的步骤指引做一个求和操作：

1. 筛选出 arr 里大于 2 的数字
2. 将步骤1中筛选出的这些数字逐个乘以 2
3. 对步骤 2 中的偶数数组做一次求和

当然啦，1、2都只是过程，我想要的只有步骤3的求和结果而已。

从一个朴素的视角出发，我可以实现如下的计算过程：

// 用于筛选大于2的数组元素
const biggerThan2 = num => num > 2  
// 用于做乘以2计算
const multi2 = num => num * 2    
// 用于求和
const add = (a, b) => a + b   

// 完成步骤 1
const filteredArr = arr.filter(biggerThan2)    
// 完成步骤 2
const multipledArr = filteredArr.map(multi2)    
// 完成步骤 3
const sum = multipledArr.reduce(add, 0)

然而，作为一个好的程序员，“能用”只是最基本的代码标准。在此基础上，我们还需要兼顾代码的质量。

代码质量衡量是一个相对宏大的命题。这里我们的例子比较简单，不需要整太多花活，只需要考虑最基础的两个要素——简洁否？安全否？

首先，代码是否简洁？答案是【否】。

我们的目标输出只有 sum 这一个求和结果，计算过程中额外定义的 filteredArr 、 multipledArr 完全属于混淆视听的冗余常量，它们拉垮了代码的可读性。

一旦我走出了当前的代码块，我将不会在任何地方再用到filteredArr和multipledArr——它们唯一的作用，就是作为入参，辅助 sum 的求和。像这样的值，我们可以记为“计算中间态”。

其次，代码是否安全？答案是【否】。

filteredArr 和 multipledArr 作为引用类型，完全有可能在运行过程中被修改。

链式调用

那么该如何解决这两个问题呢？

我们可以借助链式调用构建声明式数据流

大家知道，像 map、reduce、filter 这些数组方法，它们彼此之间是可以进行链式调用的。

因此，我们完全可以把楼上的啰嗦代码改写为如下风格：

const sum = arr.filter(biggerThan2).map(multi2).reduce(add, 0)

链式调用的每一步，都会像传送带一样，把上一步的输出作为下一步的输入“传送”出去。

借助链式调用，足以完美地规避掉那些尴尬的“中间态”，从而确保我们的代码简洁安全。

同时，链式调用也大大改善了代码的可读性：

过去，我有三行代码，我需要逐行阅读、理解计算中间态和主流程之间的逻辑关系，才能够推导出程序的意图。这样的代码，是命令式的。

现在，我只需要观察一个函数调用链，这个调用链如同一条传送带一般，用函数名标注了每道工序的行为。即便不清楚数据到底是如何在“传送带”上流转的，我们也能够通过函数名去理解程序的意图。

这样的代码，是声明式的。 基于此构建出的数据流，就是声明式的数据流。

实现声明式的数据流，除了借助链式调用，还可以借助函数组合。

链式调用的前提

链式调用虽然牛，可它不是万金油。

map()、reduce()、filter() 这些方法之间，之所以能够进行链式调用，是因为：

1. 它们都挂载在 Array 原型的 Array.prototype 上
2. 它们在计算结束后都会 return 一个新的 Array
3. 既然 return 出来的也是 Array，那么自然可以继续访问原型 Array.prototype 上的方法

也就是说，链式调用是有前提的。

链式调用的本质 ，是通过在方法中返回对象实例本身的 this/ 与实例 this 相同类型的对象，达到多次调用其原型（链）上方法的目的。

要对函数执行链式调用，前提是函数挂载在一个靠谱的宿主 Object 上。

那么对于那些没有挂载在对象上的函数（为了区分,称“独立函数”）来说，链式调用这条路显然走不通了，有没有其它的路子可以走呢？

有，那就是组合。

回调地狱

为了减少不必要的理解成本，这里我直接定义几个极简的独立函数，代码如下：

function add4(num) {
  return num + 4
}  

function mutiply3(num) {
  return num*3
}  

function divide2(num) {
  return num/2
}

问：如何基于这些独立函数，构建一个多个函数串行执行的工作流？

答：套娃！

多说无益，我直接贴出套娃代码：

const sum =  add4(mutiply(divide2(num)))

套娃，顾名思义，就是把函数的执行结果套进下一个函数里作为入参，然后再把下一个函数的执行结果作为下下一个函数的执行结果作为入参…

有多少层嵌套，就需要重复多少次这个过程。

当嵌套层级很深的时候，光是确认哪个括号对应哪个函数，就需要花上半天时间。

这场要命的套娃灾难，实际上有一个更贴切的名字，叫做“回调地狱”。

到这里我们已经引出了函数组合的目标：组合多个独立函数，构造声明式的数据流。

过程中也拜访了隔壁 OOP 世界的成功人士：链式调用。

同时，我们也遇到了组合过程中的最大问题：套娃（回调地狱）。

那么如何用魔法打败魔法，用函数式的姿势解决函数嵌套过深的问题呢？

那就是我们上面的reduce，下一节我们将讲解 reduce具体的解法。

深入函数组合思想

借助 reduce 推导函数组合

事已至此，我们重新审视一遍 reduce 的工作流示意：

在上一节的末尾，曾经这样疯狂暗示了大家一波：

咱就是说，有没有可能咱们把 pipeline 里的每一个函数也弄成不一样的呢？

更直白地说，你reduce()既然都能组合参数了，你能不能帮我的 pipeline 组合一下函数呢？

毕竟，JS 的函数是可以作为参数传递的嘛！

一旦我们可以把 reduce pipeline 里的最小计算单元修改成任意不同的函数，那么这个工作流就会变成下面这样了：

这个流程，恰恰就是一个函数组合的 pipeline。

也就是说，只要我们能够想办法让 reduce 工作流里的计算单元从一个函数转变为 N 个函数，我们就可以达到函数组合的目的。

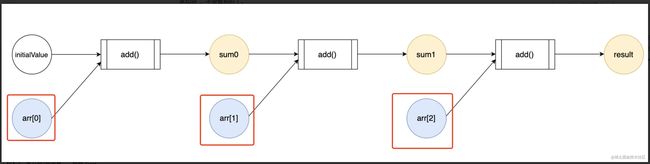
大家知道，在整个 reduce 的工作流中，callback 是锁死的，但每次调用 callback 时传入的参数是动态可变的（如下图）。

这些动态可变的参数，来自 reduce 的宿主数组。

之前介绍 reduce 时，我们用了一个塞满数字的数组作为示例。

但其实，数组的元素可以是任何类型——包括函数类型。

我们把待组合的函数放进一个数组里，然后调用这个函数数组的 reduce 方法，就可以创建一个多个函数组成的工作流。

而这，正是市面上主流的函数式库实现 compose/pipe 函数的思路。

借助 reduce 推导 pipe

顺着这个思路，我们来考虑这样一个函数数组：

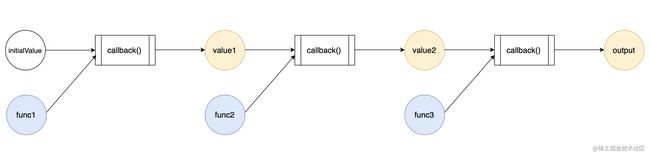
const funcs = [func1, func2, func3]

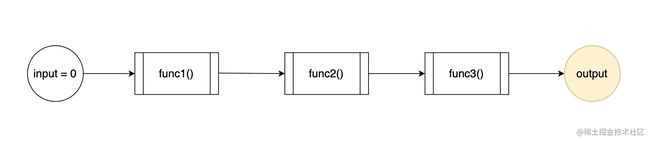
我们假设三个 func 均是用于数学计算的函数，整个工作流的任务就是吃进一个数字 0 作为入参、吐出一个计算结果作为出参。

我想要逐步地组合调用 funcs 数组里的函数，得到一个这样的声明式数据流：

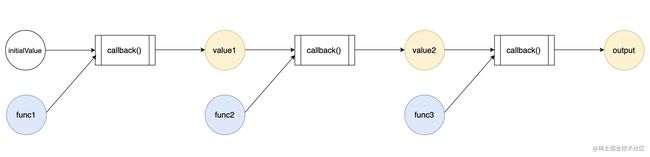
如果我借助了 reduce，我得到的数据流乍一看和楼上是有出入的：

如何通过调整 reduce 的调用，使它的工作流和声明式数据流看齐呢？

首先是入参的对齐，这个比较简单，我们只需要把 initialValue 设定为 0 就可以了。

入参明确后，我的 reduce 调用长这样：

const funcs = [func1, func2, func3]  

funcs.reduce(callback, 0)

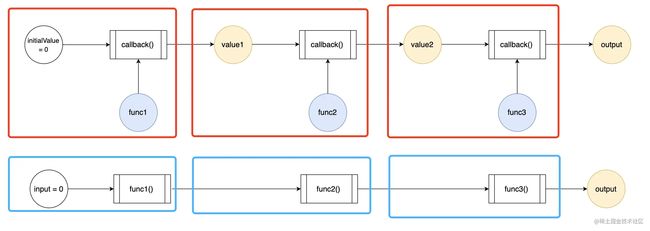
接下来重点在于 callback 怎么实现。其实我们只需要把楼上两张图放在一起做个对比，答案就呼之欲出了：

图中我用红笔对 reduce 流程做了拆分，用蓝笔对目标数据流做了拆分。

想要让上下两个流程等价，我们只需要确保红蓝两个圈圈的工作内容总是等价就可以了。

从第一对红蓝圈圈开始看起，蓝色圈圈的工作内容是 func1(0)，红色圈圈的工作内容是 callback(0, func1)。

两者等价，意味着 callback(0, func1) = func1(0)。

同理，我们可以逐步推导出第二个、第三个红色圈圈的工作内容，分别应该满足：

callback(value1, func2) = func2(value1)

callback(value2, func3) = func3(value2)

以此类推，对于任意的入参 (input, func），callback 都应该满足：

callback(input, func) = func(input)

推导至此，我们就得到了 callback 的实现：

function callback(input, func) {
  func(input)
}  

funcs.reduce(callback,0)

再稍微包装一下，给这坨逻辑起一个新名字：

function pipe(funcs) {
  function callback(input, func) {
    return func(input)
  }  

  return function(param) {
    return funcs.reduce(callback,param)
  }
}

我们就得到了一个经典的 pipe 函数。

美中不足的是手动构造数组有点麻烦，我们可以直接使用展开符来获取数组格式的 pipe 参数：

// 使用展开符来获取数组格式的 pipe 参数
function pipe(...funcs) {
  function callback(input, func) {
    return func(input)
  }  

  return function(param) {
    return funcs.reduce(callback,param)
  }
}

由此我们就可以向 pipe 传入任意多的函数，组合任意长的函数工作流了：

function add4(num) {
  return num + 4
}  

function mutiply3(num) {
  return num*3
}  

function divide2(num) {
  return num/2
}

const compute = pipe([add4, mutiply3, divide2])
// 输出 21
console.log(compute(10))

const funcFlow = pipe(method1, method2, method3, method4,...., methodN)

至此，我们便实现了一个通用的 pipe 函数。

compose：倒序的 pipe

pipe 用于创建一个正序的函数传送带，而 compose 则用于创建一个倒序的函数传送带。

我们把 pipe 函数里的 reduce 替换为 reduceRight，就能够得到一个 compose：

// 使用展开符来获取数组格式的 pipe 参数
function compose(...funcs) {
  function callback(input, func) {
    return func(input)
  }  

  return function(param) {
    return funcs.reduceRight(callback,param)
  }
}

使用 compose 创建同样的一个函数工作流，我们需要把入参倒序传递，如下：

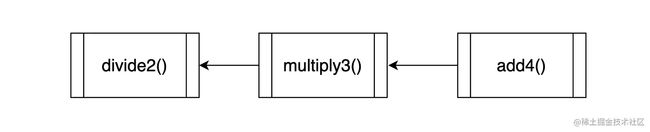
const compute = compose(divide2, mutiply3, add4)

组合后的流水线顺序，和传参的顺序是相反的。也就是说执行 compute 时，函数的执行顺序是这样的：

正序是 pipe，倒序是 compose。

pipe 和 compose 的辨析，本身也是一个热门的考察点。在面试场景下，大家一定要听清楚面试官的要求，写代码前先确认需求是【Pipe–> 】一系列函数还是【Compose<–】一系列函数。

Why Compose?

面向对象的核心在于继承，而函数式编程的核心则在于组合。

我们常说函数式编程就像一个乐高游戏：那一个个独立内聚的函数就像一堆乐高积木方块儿。

它们看似渺小到无足轻重，却可以在组合后变幻出千百种形态、最终呈现出复杂而强大的功能。

组合这个动词，赋予了函数式编程无限的想象力和可能性。

在函数式编程的实践中，我们正是借助 compose 来组合多个函数的功能，它是函数式编程中最有代表性的一个工具函数，所以它才会成为面试题中的常客。

在编码层面，如果不喜欢 reduce，你还可以借助循环、递归等姿势来实现 compose。

这里选取了 reduce，一方面是因为它足够主流（市面流行的函数式编程库 ramda 也采取了基于 reduce 的实现），另一方面也是因为它足够巧妙。

巧妙到什么程度呢？在实际的编码和面试中，基于 reduce 的 compose 几乎是理解成本最高、同时也是许多同学避之不及的一个版本。

许多能力是可以向下兼容的，包括 compose 的实现。

我相信对多数同学来说，读懂一段循环代码或者递归代码都不会是特别难的事情。

然而，如果你之前没有刻意练习过从 reduce 到 compose 的推导过程，那么第一次见到类似代码的时候，即便能够勉强理解代码的意图，也未必能够灵机一动把眼前的 reduce 调用和函数组合联系起来。

但经过了近几节的学习，相信大家早已对 reduce 刮目相看了。

当你再次在别人写的代码中见到 reduce 时，脑海中闪现的关键字除了“数组、斐波那契”等等之外，不要忘了还有“函数组合”。

“多元函数”解决方案

偏函数和柯里化堪称面试场上的“老八股”了

当偏函数和柯里化出现在大家视野里的时候，它更多地是作为一道“名词解释题”，而非一个“编码工具”。

然而要想理解偏函数和柯里化，最简单的姿势其实恰恰是从“编码工具”这个角度切入。

本节我们就将从“编码工具”的角度来认识它们。

认识一个锤子，我们首先要知道它可以被用来对付哪些钉子。

认识一个编码工具，我们首先要知道它可以被用来解决哪些问题。

偏函数和柯里化解决的最核心的问题有两个，分别是：

• 函数组合链中的多元参数问题
• 函数逻辑复用的问题

函数组合链中的多元参数问题

函数组合虽好，但各种限制少不了。简单回顾一下上节我们徒手撸过的 Pipe 函数：

// 使用展开符来获取数组格式的 pipe 参数
function pipe(...funcs) {
  function callback(input, func) {
    return func(input)
  }  

  return function(param) {
    return funcs.reduce(callback,param)
  }
}

当时给出的调用示例是这样的：

// 一元函数，一个入参
function add4(num) {
  return num + 4
}  

// 一元函数，一个入参
function multiply3(num) {
  return num*3
}  

// 一元函数，一个入参
function divide2(num) {
  return num/2
}

const compute = pipe(add4, multiply3, divide2)

这个属于是理想情况了，有的时候一个调用链中的函数彼此之间可能并没有这么和谐。

举个例子，假如说做乘法的时候并没有一个 multiply3， 只有一个乘数和被乘数都可以自定义的函数，如下：

function multiply(x, y) {
  return x * y
}

一元函数 multiply3 变成了二元函数 multiply，此时若是把 multiply 直接丢回 pipe 链中去，那结果指定是不对的：

const compute = pipe(add4, multiply, divide2)
// 输出 NaN
compute(20)

为啥呢？当然是因为咱的 reduce callback 只能消化一个入参啦：

function callback(input, func) {
  return func(input)
}  

当执行到 callback(input, multiply) 时，multiply 函数期望可以接收 2 个 number 类型的入参，但实际调用时却只传入了一个 number 类型的入参：

multiply(input)

这个调用等价于：

multiply(input, undefined)

一个数字乘以 undefined，结果自然是 NaN 啦。

对于函数组合链来说，它总是预期链上的函数是一元函数：

函数吃进一个入参，吐出一个出参，然后这个出参又会作为下一个一元函数的入参…参数个数的对齐，是组合链能够运转的前提。

一旦链上乱入了多元函数，那么多元函数的入参数量就无法和上一个函数的出参数量对齐，进而导致执行错误。

这也就是我们所说的“参数对齐”问题。

这可咋办呢？

任何时候，只要我们想要对函数的入参数量进行改造，必须先想到偏函数&柯里化。

求解多元参数问题

先来说说柯里化，维基百科中对柯里化有着这样的定义：

在计算机科学中，柯里化（英语：Currying），又译为卡瑞化或加里化，是把接受多个参数的函数变换成接受一个单一参数（最初函数的第一个参数）的函数，并且返回接受余下的参数而且返回结果的新函数的技术。

通俗来讲，它是这个意思： 柯里化是把 1 个 n 元函数改造为 n 个相互嵌套的一元函数的过程。

再具体一点，就是说柯里化是一个把 fn(a, b, c)转化为fn(a)(b)(c)的过程。

举个例子，有一个函数可以将任意三个数相加：

function addThreeNum(a, b, c) {
  return a + b + c
}

正常调用的话就是 addThreeNum(1, 2, 3) ，但是通过柯里化可以把调用改造为 addThreeNum(1)(2)(3)。

如何做到呢？ 一个最直接的想法是在原有的函数上做改造，像这样：

// 将原函数改造为三个嵌套的一元函数
function addThreeNum(a) {
  // 第一个函数用于记住参数a
  return function(b) {
    // 第二个函数用于记住参数b
    return function(c) {
      // 第三个函数用于执行计算
      return a + b + c
    }
  }
}

// 输出6，输出结果符合预期
addThreeNum(1)(2)(3)

但是，在设计模式中强调过“开放封闭”原则——对拓展开放，对修改封闭。

直接修改现有函数，显然违背了这一原则。

有没有什么姿势，可以允许在保留原有函数的基础上，单纯通过增量代码来实现柯里化呢？

当然有啦！高阶函数不就是干这个的么！

下面就针对加法这个场景，创建了一个名为 curry 的高阶函数（解析在注释里）：

// 定义高阶函数 curry
function curry(addThreeNum) {
  // 返回一个嵌套了三层的函数
  return function addA(a) {
    // 第一层“记住”参数a
    return function addB(b) {
      // 第二层“记住”参数b
      return function addC(c) {
        // 第三层直接调用现有函数 addThreeNum
        return addThreeNum(a, b, c)
      }
    }
  }
}

// 借助 curry 函数将 add
const curriedAddThreeNum = curry(addThreeNum)
// 输出6，输出结果符合预期
curriedAddThreeNum(1)(2)(3)

偏函数 VS 柯里化

在理解了柯里化的基础上，理解偏函数就是小菜一碟了。

这里为了体现对专业术语的respect，我仍然是象征性地先放一段维基百科的解释：

在计算机科学中，部分应用（或部分函数应用）指的是将一些参数固定在一个函数上，产生另一个较小元的函数的过程。

tips: 偏函数英文是 partial application， 直译过来就是“部分应用”。

这个定义其实并不难懂，通俗来说：

偏函数是指通过固定函数的一部分参数，生成一个参数数量更少的函数的过程。

• 柯里化说的是一个 n 元函数变成 n 个一元函数。
• 偏函数说的是一个 n 元函数变成一个 m(m < n） 元函数。
• 对于柯里化来说，不仅函数的元发生了变化，函数的数量也发生了变化（1个变成n个）。
• 对于偏函数来说，仅有函数的元发生了变化（减少了），函数的数量是不变的。

也就是说对于一个调用姿势长这样的四元函数来说：

func(a, b, c, d)

我们可以固定第一个入参，使其缩减为一个三元函数：

func(b, c, d)

也可以固定前两个入参，使其缩减为一个二元函数：

func(c, d)

总之，只要它的元比之前小，就满足了偏函数的要求。

接下来我们来看一下，偏函数如何求解组合链中的参数对齐问题？

偏函数的实现思路是固定一部分函数参数，这里延续高阶函数的思路，对现有函数进行一定的“包装”来达到目的：

// 定义一个包装函数，专门用来处理偏函数逻辑
function wrapFunc(func, fixedValue) {
  // 包装函数的目标输出是一个新的函数
  function wrappedFunc(input){
    // 这个函数会固定 fixedValue，然后把 input 作为动态参数读取
    const newFunc = func(input, fixedValue)
    return newFunc
  }
  return wrappedFunc
}
const multiply3 = wrapFunc(multiply, 3)

// 输出6
multiply3(2)

这样就成功固定了 multiply 函数的第一个入参 x，得到了一个一元函数 multiply3，这完全符合组合链对函数元的预期。

函数逻辑复用问题

当我们看到偏函数和柯里化的实现分别都借助了高阶函数后，“逻辑复用”几乎是一件不言而喻的事情了。

参数固定-复用存量逻辑

在 multiply3 这个例子中，偏函数除了解决了函数的元的问题，还充分地对现有逻辑进行了复用。

multiply 函数是一个存量函数，我们的目标函数 multiply3 其实可以看作是 multiply 函数功能的一个子集。

这种情况下，与其单独定义一个 multiply3，不如试着通过偏函数处理实现对存量逻辑 multiply 的定制。

multiply3、multiply 两个函数的逻辑都不算复杂，复用带来的利好体现得还不算特别明显。

但在实际的应用中，存量函数逻辑可以是非常复杂的。

比如在业务逻辑中的一个处理订单数据的函数：

function generateOrderData(type, area, settlement) {
  // 省略数十行难以理解的业务逻辑......
}

generateOrderData 通过读取订单类型、订单地区、订单结算信息等参数，对订单信息进行重构，最终输出一套能够供 UI 层直接消化的渲染数据。

这样一个函数的改造成本是很高的。

如果我们遇到一个场景，期望能够针对某一个特定区域、特定类型的订单数据进行计算（也就是固定 type、area 这两个参数），对应函数名为 generateSpecOrderData(settlement)。

相比于参考 generateOrderData 的具体逻辑重新写一个 generateSpecOrderData 出来，直接在 generateOrderData 的基础上做偏函数处理不仅可以帮助我们避免大量的重复代码，同时也省去了读函数、理解函数的时间成本——毕竟，做偏函数处理只需要我们了解函数的入参规则就可以了。

缩小函数的元数-减少重复传参

偏函数不仅仅可以帮我们减少定义函数时的重复代码，还可以帮我们减少调用函数时的重复传参。

在 generateSpecOrderData 函数被定义出来之前，在项目里见到了大量这样的代码：

// 文件 a
const res = generateOrderData('food', 'hunan', settelment)

// 文件 b
const UIData = generateOrderData('food', 'hunan', settelment)  

// 文件 c  
const result = generateOrderData('food', 'hunan', settelment)  

不同的调用，重复的传参，重复的 food + hunan。

而偏函数恰恰就可以把 food 和 hunan “记忆”下来，帮助我们避免这些重复。

实际上，通用函数为了确保其自身的灵活性，往往都具备“多元参数”的特征。

但在一些特定的业务场景下，真正需要动态变化的只是其中的一部分的参数。

这时候函数的一部分灵活性对我们来说是多余的，我们反而希望它的功能具体一点。

比如 generateSpecOrderData 函数，就对 type 和 area 并不感冒，只是想动态传入 settlement 而已。

这种场景下，偏函数出来扛大旗就再合适不过了。

至此，我们已经通过一些实例理解了偏函数和柯里化两者的概念和用途，并且结合函数组合链的例子，对偏函数解决问题的方式有了具体的认知。

偏函数和柯里化是一脉相承的，它们解决的其实是同一类问题。

也就是说函数组合链的参数对不齐问题，用柯里化也是可以解决的，并且柯里化也能够协助我们更好地复用函数逻辑。

如何证明这一点呢？在下一节会给出答案，并且一起实现一个通用的柯里化函数。

柯里化：构造一个通用函数

上回说到，柯里化和偏函数一脉相承，两者解决的其实是同一类问题，也就是“调整函数的元”的问题。

我们同时提到了柯里化和偏函数都能够促进“逻辑的复用”，这是因为调整存量函数的元、生成新函数、减少重复传参的这整个过程，本身就是一个逻辑复用的过程，并且很多时候是以高阶函数的形式实现的。

本节我们把重点放在柯里化上。

柯里化解决 multiply 函数的参数问题

既然偏函数和柯里化解决的都是函数的元的问题，那么 multiply 函数一元化为 multiply3 也能够用柯里化求解。

// 一元函数，一个入参
function multiply(x, y) {
  return x * y
}

// 定义一个包装函数，专门用来处理偏函数逻辑
function curry(func) {
  // 逐层拆解传参步骤 - 第一层
  return function(x){
    // 逐层拆解传参步骤 - 第二层
    return function(y) {
      // 参数传递完毕，执行回调
      return func(x, y)
    }
  }
}
const multiply3 = curry(multiply)(3)

// 输出6
multiply3(2)

柯里化的“套路”

柯里化函数的特征，在于它是嵌套定义的多个函数，也就是“套娃”。

因此，柯里化的实现思路，我愿称之为“套娃之路”，简称“套路”。

这个“套路”有多深？截至目前来看，完全取决于原函数的参数个数。

比如我们的第一个柯里化示例，它是三元函数，就相应地需要套三层：

function curry(addThreeNum) {
  // 返回一个嵌套了三层的函数
  return function addA(a) {
    // 第一层“记住”参数a
    return function addB(b) {
      // 第二层“记住”参数b
      return function addC(c) {
        // 第三层直接调用现有函数 addThreeNum
        return addThreeNum(a, b, c)
      }
    }
  }
}

而本节柯里化 multiply 函数，由于此函数是二元函数，curry 就只需要两层：

function curry(func) {
  // 第一层“记住”参数x
  return function(x){
    // 第二层“记住”参数y
    return function(y) {
      // 参数传递完毕，执行回调
      return func(x, y)
    }
  }
}

这样看来，似乎 curry 函数怎么写，还得先看回调函数的入参有几个。

如果我的一个应用程序里，有二元函数、三元函数…甚至 n 元函数，它们都想被柯里化，那岂不是要写不计其数个 curry 函数来适配每一个元数了？

这属于是暴力枚举了，这很不函数式呀。

有没有可能， curry 函数内部可以结合入参的情况，自动判断套娃要套几层呢？

话都说到这儿了，咱也就引出了本节的重点，同时也是面试的重点——通用柯里化函数的实现。

通用柯里化函数：自动化的“套娃”

思路分析

通用的 curry 函数应该具备哪些能力？最关键的一点，它要能“自动套娃”。

也就是说，不管我传入的函数有多少个参数，curry 都应该能分析出参数的数量，并且动态地根据参数的数量自动做嵌套。

我们简单拆解一下这个函数的任务：

1. 获取函数参数的数量
2. 自动分层嵌套函数：有多少参数，就有多少层嵌套
3. 在嵌套的最后一层，调用回调函数，传入所有入参。

获取函数参数的数量

首先第一步，获取函数参数的数量。

这个简单，在 JS 里，函数作为一等公民，它和对象一样有许多可访问的属性。其中 Function.length 属性刚好就是用来存放函数参数个数的。

通过访问函数的 length 属性，就可以拿到函数参数的数量，如下：

function test(a, b, c, d) {
}

// 输出 4
console.log(test.length)

自动化“套娃”

给定一个嵌套的上限，期望函数能够自动重复执行嵌套，直至达到上限。

而“嵌套”的逻辑，摊开来看的话无非是：

1. 判断当前层级是否已经达到了嵌套的上限
2. 若达到，则执行回调函数；否则，继续“嵌套”

在嵌套函数内部继续嵌套，相当于是“我调用我自己”。而“我调用我自己”有个学名，叫做“递归”。

没错，这里，我们正是借助递归来实现所谓的“自动化套娃”。

递归边界的判定

curry 函数会在每次嵌套定义一个新的函数之前，先检查当前层级是否已经达到了嵌套的上限。

也就是说每一次递归，都会检查当前是否已经触碰到了递归边界。

一旦触碰到递归边界（嵌套上限），则执行递归边界逻辑（也就是回调函数）。

那么这个递归边界怎么认定呢？

柯里化的过程，是层层“记忆”每个参数的过程。每一层嵌套函数，都有它需要去“记住”的参数。如果我们递归到某一层，发现此时已经没有“待记忆”的参数了，那么就可以认为，当前已经触碰到了递归边界。

明确了这三个任务的解法，我们就可以开始写代码啦！

编码实现

// curry 函数借助 Function.length 读取函数元数
function curry(func, arity=func.length) {
  // 定义一个递归式 generateCurried
  function generateCurried(prevArgs) {
    // generateCurried 函数必定返回一层嵌套
    return function curried(nextArg) {
      // 统计目前“已记忆”+“未记忆”的参数
      const args = [...prevArgs, nextArg]  
      // 若 “已记忆”+“未记忆”的参数数量 >= 回调函数元数，则认为已经记忆了所有的参数
      if(args.length >= arity) {
        // 触碰递归边界，传入所有参数，调用回调函数
        return func(...args)
      } else {
        // 未触碰递归边界，则递归调用 generateCurried 自身，创造新一层的嵌套
        return generateCurried(args)
      }
    }
  }
  // 调用 generateCurried，起始传参为空数组，表示“目前还没有记住任何参数”
  return generateCurried([])
}

柯里化解决组合链的元数问题

接下来我们就借助一个函数元数五花八门的组合链，来验证一下通用 curry 函数的效果。

首先定义一系列元数不等、且不符合一元要求的算术函数：

function add(a, b) {
  return a + b
}

function multiply(a, b, c) {
  return a * b * c
}

function addMore(a, b, c, d) {
  return a + b + c + d
}

function divide(a, b) {
  return a / b
}

此时若像下面这样直接把四个函数塞进 pipe 中去，必定是会倒沫子的：

const compute = pipe(add, multiply, addMore, divide)

我们需要首先对四个函数分别作“一元化”处理。

这“一元化”处理的第一步，就是借助 curry 函数把它们各自的传参方式重构掉：

const curriedAdd = curry(add)
const curriedMultiply = curry(multiply)
const curriedAddMore = curry(addMore)
const curriedDivide = curry(divide)

然后对这些函数逐个传参，传至每个函数只剩下一个待传参数为止。这样，我们就得到了一堆一元函数：

const compute = pipe(
  curriedAdd(1), 
  curriedMultiply(2)(3), 
  curriedAddMore(1)(2)(3), 
  curriedDivide(300)
)

试着调用一下 compute，结果符合预期。至此，我们的通用柯里化函数便已完成。