[Python|最优状态估计与滤波学习笔记] 最小均方滤波，卡尔曼滤波，神经网络滤波

前言—最优状态估计与滤波

卡尔曼滤波器在Python的filterpy模块里面全都有：线性卡尔曼，扩展卡尔曼和无极卡尔曼。这里记录自己的学习。

1、最小均方滤波（Least Mean Square, LMS）

基本原理

最小均方滤波大致思路：对于一大段受到噪声干扰的数据，如果能从中获取到一小段不含噪声的理想数据，则可以通过理想数据和受干扰的数据训练出来一个滤波器，这个滤波器通过学习可以自己滤掉干扰噪声。这和神经网络或者机器学习有相似的地方。原理图如下所示：

d(n)为理想数据序列，w(n)为实际数据序列。

LMS设计步骤

对于LMS滤波器，首先提几个很重要的参数：滤波器的阶数—ord（有的也叫抽头）、训练步长train_len，学习率learning_rate，后面一一用到再介绍。现在假设有一个包含噪声的序列X，然后还知道序列X中X(1)~X(m)（假设序列编号是从1开始，且X是列向量）这一段序列的真实值为X_ideal。则设计LMS滤波器的步骤为：

• 1、首先初定一个阶数ord和训练步长train_len(随便确定两个整数即可，但要求满足ord+train_len<=m)；
• 2、定义一个权值矩阵(列向量)W，大小为（ord，1），初值全部设置为0；
• 3、计算序列X的自相关矩阵，即：A = X*tranpose(X)，同时计算矩阵A的最大特征值eigA_max，则学习率learning_rate = 1/abs(eigA_max)；
• 4、接下来则开始一个循环：

  for (i=1；i<=train；i++)
  		W = W - 2*learning_rate*(tranpose(X(i：i+ord))*W-X_ideal(i:i+ord))
  

  循环结束后的W即为训练完的权值矩阵。
• 5、最后，利用训练完的权值矩阵则直接可以对X序列进行滤波了，即：

  X_ideal(k) = tranpose(X(k-ord,k))*W
  

上面可以看出，滤波输出为当前测量值和之前若干测量值的加权求和，这种权值就是通过学习训练得到，尤其是第4步更新权值的算法，就是梯度下降，这种过程和神经网络的训练很类似。这里的性能函数为：

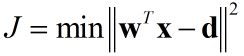
仿真代码

这里序列是1000个数据点，用于训练的数据点是125个。

import numpy as np
import matplotlib.pyplot as plt


class LMSFilter():
    def __init__(self, ideal_sequence, real_sequence, filter_ord, learning_rate, train_len):
        '''
        :param ideal_sequence:理想输出序列
        :param real_sequence:实际输出序列
        :param filter_ord:滤波器阶数
        :param learning_rate:学习率
        :param train_len:训练长度
        '''
        self.ideal_sequence = ideal_sequence
        self.real_sequence = real_sequence
        self.filter_ord = filter_ord
        self.learning_rate = learning_rate
        self.train_len = train_len
        self.__Train()

    def __Train(self):
        self.W = np.zeros(self.filter_ord)#权值矩阵
        for i in range(self.filter_ord - 1, self.filter_ord + self.train_len):
            measured = self.real_sequence[i - self.filter_ord + 1: i+1]
            y_ideal = self.ideal_sequence[i]
            y_real = np.matmul(measured, self.W)
            error = y_real - y_ideal
            self.W = self.W - 2*self.learning_rate*error*measured

    def Filter(self):
        '''
        :return:返回滤波值和滤波误差
        '''
        self.y_filtered = np.zeros(len(self.real_sequence))#定义一个矩阵存放滤波后的值
        self.y_filtered[:] = None#初始化，用于训练的数据段不需要输出。
        for i in range(self.filter_ord + self.train_len, len(self.real_sequence)):
            measured = self.real_sequence[i - self.filter_ord + 1: i+1]
            self.y_filtered[i] = np.matmul(measured, self.W)
        self.error = self.ideal_sequence - self.y_filtered
        return self.y_filtered, self.error


if __name__=="__main__":
    t = np.linspace(0,10,1000)#时间序列
    noise = 50*np.random.randn(1000)#噪声序列
    X_ideal = 100*np.sin(t)#理想序列
    Measured = X_ideal + noise#实际测量序列
    A = np.array([Measured])#求输入序自相关矩阵的特征值
    B = np.matmul(np.transpose(A),A)
    Eig = np.linalg.eig(B)
    learning_rate = 1/max(abs(Eig[0]))#学习率取最大特征值的倒数
    Example = LMSFilter(X_ideal, Measured, 25, learning_rate, 100)#初始化一个LMS，并开始训练
    Filtered, Error = Example.Filter()#返回寻训练后的LMS滤波器
    F1, = plt.plot(t, Measured, color='r')
    F2, = plt.plot(t, Filtered, color='b')
    F3, = plt.plot(t, X_ideal, color='k')
    F4, = plt.plot(t, Error, color='y')
    plt.legend(handles=[F1, F2, F3, F4], labels=['Measured', 'Filtered', 'Ideal', 'Error'])
    plt.show()

结果：

可以发现前面有125个点没有输出，这些点用于训练了，所以不拿来再作为测试数据（类似神经网络里面的测试集和训练集）。可以发现，滤波效果有，但不是很好，这里的噪声为平稳随机噪声。LMS的几个参数对滤波效果有很大的影响，可以自己改改相应试一试。

2、线性卡尔曼滤波（Linear Kalman Filter, KF）

使用示例

考虑一个真实的物理系统：一辆汽车，当汽车运动起来后，车就具有速度，同时车在大地坐标系的位置也会发生改变。现在，考虑这样一个问题。如果有一套GPS安装在车上面，就可以实时获得车辆的坐标和速度。但是，对于任何一个测量信号入股不进行滤波的话将会有噪声成分干扰测量。此外，GPS是一种低频信号（10Hz左右），想想当汽车以120km/h速度行驶时候，在120/3.6x0.1=3.3m内是无法知道汽车的真实位置。因此，卡尔曼滤波器一个很重要的应用就是GPS与惯导的融合（GPS与IMU融合介绍）。接下来，就以这种融合做一个很简单线性卡尔曼滤波的示例（示例很简单，并不是严格的GPS与IMU融合）。

基本步骤

线性卡尔曼滤波器是一种基于模型的滤波器，在使用时必须建立起研究对象相对精确的状态空间方程。线性卡尔曼滤波的理论推导网上很多，这里不重复。卡尔曼的基本步骤是“计算先验状态和协方差”—>“计算卡尔曼增益”—>“计算后验状态和协方差”。

仿真模型

仿真模型为一个在平面二维运动汽车，汽车的状态有X坐标，Y坐标，X方向速度和Y方向速度，这里假设利用GPS测量汽车的坐标信息，利用IMU测量汽车的加速度Ax和Ay。汽车运动方程具体矩阵A、B、C参数见程序[Main.py]

# Main.py
# linear system
# X(k + 1) = AX(k) + BU(k)
# Y(K + 1) = CX(k + 1)
from LKFilter import *
import matplotlib.pyplot as plt
import math

if __name__=="__main__":
    T = 0.01#时间采样步长
    N = 0#计数器，乘以T后用来输出连续时间
    A = np.matrix([1, 0, T, 0, 0, 1, 0, T, 0, 0, 1, 0, 0, 0, 0, 1]).reshape(4, 4)#状态矩阵
    B = np.matrix([0.5 * T ** 2, 0, 0, 0.5 * T ** 2, T, 0, 0, T]).reshape(4, 2)#输入矩阵
    C = np.matrix([1, 0, 0, 0, 0, 1, 0, 0]).reshape(2, 4)#输出矩阵
    I = np.eye(4)#单位矩阵
    Q = np.diag((0.0, 0.0, 0.0, 0.0))#系统噪声协方差矩阵
    R = np.diag((0.1, 0.1))#测量噪声协方差矩阵
    X_est = np.matrix([0.0, 0., 0.0, 0.]).reshape(4, 1)  # 后验状态初始化
    X_pre = np.matrix([0., 0., 0., 0.]).reshape(4, 1)  # 先验状态初始化
    X_true = np.matrix([0., 0., 0., 0.]).reshape(4, 1)  # 真实状态初始化
    Y_observed = np.matrix([0., 0.]).reshape(2, 1)  # 测量值初始化
    P0 = np.diag((10, 10, 0, 0))  # 初始状态协方差矩阵

    Example = KFilter(A, B, C, Q, R, T, P0, X_true, X_est)#实例化一个线性卡尔曼滤波器

    while True:
        N+=1
        Ax = 30 * np.sin(2 * math.pi * N*T)#x方向加速度
        Ay = 90 * np.cos(2 * math.pi * N*T)#y方向加速度
        U = np.array([Ax, Ay]).reshape(2, 1)#组合成输入向量
        W = np.matmul(np.sqrt(Q), np.random.randn(4).reshape(4, 1))#系统噪声矩阵，这里放在while循环里面，每次都可以产生一个随机矩阵
        V = np.matmul(np.sqrt(R), np.random.randn(2).reshape(2, 1))#测量噪声矩阵
        '''利用上述的矩阵来构建一个仿真系统'''
        X_true_tem = np.matmul(A, X_true[:, -1]) + np.matmul(B, U) + W
        X_true = np.column_stack((X_true, X_true_tem))#真实的状态序列，这里用了column_stack，就是将每一个的更新的状态放在X_true后面，便于最后画图
        Y_observed_tem = np.matmul(C, X_true[:, -1]) + V
        Y_observed = np.column_stack((Y_observed, Y_observed_tem))
        '''调用线性Kalman滤波'''
        Result = Example.Kalman(Y_observed[:, -1], U)#这个方法的输入参数是当前时刻系统的测量值Y_observed[:, -1]和输入U，返回的是时间序列，所有时刻的观测状态与测量值
        '''画图，注意Result中返回的值属于numpy.matrix型数据不是array型，在plot的时候要转换一下'''
        plt.clf()
        plt.figure(1)
        plt.plot(np.array(Result[0][0, :])[0], np.array(Result[1][0, :])[0], label='Estimated X')
        plt.plot(np.array(Result[0][0, :])[0], np.array(Result[2][0, :])[0], label='Measured X')
        plt.plot(np.array(Result[0][0, :])[0], np.array(X_true[0, :])[0], label='Real X')
        plt.xlabel('Time[s]')
        plt.ylabel('X coordinate[m]')
        if N == 1:
            plt.legend()
        plt.figure(2)
        plt.plot(np.array(Result[1][0, :])[0], np.array(Result[1][1, :])[0], label='Estimated X-Y')
        plt.plot(np.array(Result[2][0, :])[0], np.array(Result[2][1, :])[0], label='Measured X-Y')
        plt.plot(np.array(X_true[0, :])[0], np.array(X_true[1, :])[0], label='Real X-Y')
        plt.xlabel('X coordinate[m]')
        plt.ylabel('Y coordinate[m]')
        plt.pause(0.01)
        plt.ioff()

线性卡尔曼滤波算法，文件名KFilter.py。

# Linear System Kalman Filter
# X(k + 1) = AX(k) + BU(k) + W(k)
# Y(K + 1) = CX(k + 1) + V(k)
# Developed by OldYoung
import numpy as np

class KFilter:
    def __init__(self, A, B, C, Q, R, T, P0_ini, X_true_ini, X_est_ini):
        '''
        :param A:State matrix
        :param B:Input matrix
        :param C:Transfer matrix
        :param Q:System noise covariance
        :param R:Measurement noise covariance
        :param T:Sample time
        :param P0_ini:Initial covariance matrix of state
        :param X_true_ini:Initial value of true states
        :param X_est_ini:Initial value of estimated states
        '''
        self.A = A
        self.B = B
        self.C = C
        self.Q = Q
        self.R = R
        self.A_shape = A.shape
        self.C_shape = C.shape
        self.P0 = P0_ini
        self.T = T
        self.N = 0
        self.I = np.eye(self.A_shape[0])
        self.t = np.matrix(np.zeros((1, 1)))
        self.Y_measured = np.matrix([0.] * self.C_shape[0]).reshape(self.C_shape[0], 1)
        self.Y_true = np.matrix([0.] * self.C_shape[0]).reshape(self.C_shape[0], 1)
        self.X_estimated = X_est_ini
        self.X_true = X_true_ini

    def Kalman(self, Y_measured, U):
        '''
        :param Y_measured: Measured output
        :param U:Input
        :return:[time, estimated states, measured output]
        '''
        self.N += 1
        self.t = np.column_stack((self.t, np.matrix([self.N * self.T])))
        self.Y_measured = np.column_stack((self.Y_measured, Y_measured))
        self.X_pre = np.matmul(self.A, self.X_estimated[:, -1]) + np.matmul(self.B, U)#预测
        self.P_pre = np.matmul(np.matmul(self.A, self.P0), np.transpose(self.A)) + self.Q#预测
        self.K = np.matmul(np.matmul(self.P_pre, np.transpose(self.C)),
                           np.linalg.pinv(np.matmul(np.matmul(self.C, self.P_pre), np.transpose(self.C)) + self.R))#计算卡尔曼增益
        self.X_est_tem = self.X_pre + np.matmul(self.K, self.Y_measured[:, -1] - np.matmul(self.C, self.X_pre))#校正
        self.X_estimated = np.column_stack((self.X_estimated, self.X_est_tem))
        self.P0 = np.matmul(np.matmul(self.I - np.matmul(self.K, self.C), self.P_pre),
                            np.transpose(self.I - np.matmul(self.K, self.C))) + np.matmul(np.matmul(self.K, self.R), np.transpose(self.K))#更新协方差矩阵
        return [self.t, self.X_estimated, self.Y_measured]

仿真结果

可以看到，卡尔曼滤波后的位置与真实位置很接近。

• “t—X”轴观测结果：
  
• “X—Y”坐标系观测结果：
  

线性卡尔曼的局限

上面结果表明线性卡尔曼滤波具有很好的效果。但是，线性卡尔曼是一种基于模型的滤波方法。也就是说，如果没有系统建模方程是不能用卡尔曼滤波（和LMS这些基于数据的滤波器是不一样的）。并且，如果建立的模型不够精确，也会导致卡尔曼滤波效果变差甚至发散。此外，设计滤波器的时候，系统噪声和测量噪声要求为高斯白噪声且需要知道噪声的统计信息，这在实际应用中很难满足要求。

噪声影响

为了对比，将上面程序Main.py的17、24、32行程序做一下改动，增加一个噪声R1，假设这是测量噪声的真实值，并带入测量矩阵V，但是在给滤波器实例化传递参数的时候仍然给R。可以发现，此时的卡尔曼滤波效果相对变差了一些。值得注意的是，系统噪声一直设为0，因为系统噪声本身就很难测量和估计，这里就不研究了

R = np.diag((0.1, 0.1))  # 假定测量噪声协方差矩阵
R1 = np.diag((1, 1))#真实测量噪声协方差矩阵
Example = KFilter(A, B, C, Q, R, T, P0, X_true, X_est)#实例化一个线性卡尔曼滤波器
V = np.matmul(np.sqrt(R1), np.random.randn(2).reshape(2, 1))#测量噪声矩阵

建模误差

同样，将上面程序Main.py的13、34行程序做一下改动，B看作是我们建立的模型的输入矩阵，而B1是真实模型输入矩阵。同样，用一个不精确的B去初始化卡尔曼滤波器。可以发现，此时的卡尔曼滤波器的效果变得更差，和真实值有很大的出入。

B = np.matrix([0.5 * T ** 2, 0, 0, 0.5 * T ** 2, T, 0, 0, T]).reshape(4, 2)#建模输入矩阵
B1 = np.matrix([0.5 * T ** 2, 0, 0, 0.5 * T ** 2, 1.2*T, 0, 0, T]).reshape(4, 2)#真实输入矩阵
Example = KFilter(A, B, C, Q, R, T, P0, X_true, X_est)#实例化一个线性卡尔曼滤波器
X_true_tem = np.matmul(A, X_true[:, -1]) + np.matmul(B1, U) + W

总结：线性卡尔曼滤波最早是用在航空航天领域，可以花巨资获取精确的数学模型，效果很好。但后来移植到普通工业应用时，受成本和技术限制，不能获得精确的系统模型和噪声统计特性，上述局限就暴露出来。换句话说，线性卡尔曼滤波器的鲁棒性较差（鲁棒性：控制器或观测器在系统未建模动态和不确定干扰影响下能保持较好性能的能力）。H无穷大卡尔曼滤波器正是为了提升传统卡尔曼的鲁棒性而产生的。

3、H无穷卡尔曼滤波（H-infinite KF）

4、扩展卡尔曼滤波（Extend Kalman Filter, EKF）

5、无迹卡尔曼滤波（Unscented Kalman Filter, UKF）

6、神经网络滤波（Neural Networks Filter, NNF）

持续更新中。。。