2021年数维杯数学建模A题外卖骑手的送餐危机求解全过程文档及程序

2021年数维杯数学建模

A题 外卖骑手的送餐危机

原题再现：

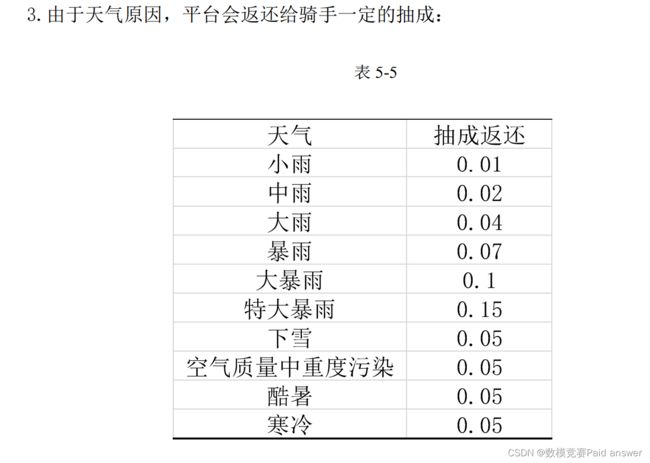
  外卖业务已经成为了大城市上班族每日生活中不可或缺的一部分。根据美团2020年6月发布的《2019中国即时配送行业发展报告》中显示，2019年我国即食配送业务订单规模达到182.8亿单，比2018年增长了37%，即时配送行业用户达到4.21亿人，比2018年增加了17.6%。面对巨大的订单量及用户群体，外卖骑手的数量也呈现一种直线上升的趋势。2019年通过美团骑手总数达到399万人，同比增长了23.3%。根据第三方平台数据显示，2020年外卖骑手的数量突破438万。面对如此庞大的外卖骑手群体，他们的收入还能达到广告中宣传的（“轻松干，月入六千；努力干，月入过万；拼命干，工资无上限”）收入吗？
  在复杂的国内与国际经济环境及我国庞大的人口规模下外卖骑手间的竞争变得异常激烈。这给予了平台更多的订单配送提成单价压缩空间。其中常以拼命压缩配送时间和延长上班时间来换取较高收入的骑手为参照，以骑手配送效率低下为理由逐步压缩外卖骑手的订单配送提成。典型表现包括当初的一单15元降到后来的8元，再到3元，再到更低的水平……。这导致外卖骑手从原来的月入过万逐步缩减到较难超过月入五千的现状。在当前条件下如果要实现月入过万的目标，则在假定平均订单配送提成3.33元的前提下每日至少需要配送超过100单的外卖，以平均每10分钟配送1单计算平均每天工作时间需要超过16小时。
  根据北大博士后陈龙的田野调查结果显示，骑手在送外卖的过程中，平台会通过智能手机、商家的无线网络等，不断地更新收集外卖骑手到达商家的时间、停留的时长，消费者住址楼层等数据。在此基础之上通过智能算法和数据分析不断压缩骑手的配送时间。而骑手为了节约时间尽快完成配送任务，出现了逆行、闯红灯等违反交通规则的现象。在平台的数据分析驱动下，外卖骑手正在向更快更廉价的趋势发展，这让他们逐渐远离了全面建成小康社会的目标。
  在外卖骑手不断抱怨的同时商家方面也对于平台高达20个点抽成叫苦不迭，其中部分商家为了盈利出现了调理包加热、食材不新鲜、包装材料廉价等问题，最终消费者也成为了受害群体。
上述种种事实表明外卖行业中存在着严重的内卷现象。数据分析至关重要，但利用数据分析来掠夺弱势群体少有的财富和时间并不可取。请你通过数学建模的方法解决外卖平台、骑手、商家与消费者之间的如下问题：
  问题1：请充分考虑骑手的骑行安全与高质量服务等因素后，试制定一个合理的骑手配送时长设计方案，并提供对应的完成质量奖惩措施。
  问题2：您能否提出一种考虑多种因素在内的静态和动态订单配送提成定价与奖惩策略，它在不显著增加订单总体配送费用与总体配送效率的基础之上，能够使得骑手总体的满意度最高。
  问题3：随着全球极端气候的频发（如暴雨、暴雪及大风等），我们需要考虑极端气候条件下的额外订单配送费用收取金额、订单配送时长设计及订单配送提成设计方案。您能否提供一个考虑上述因素的通用方案？
  问题4：共享、共赢依然成为了新的经济发展模式。在外卖骑手的送餐危机中外卖平台、骑手、商家与消费者之间显然没有实现这种共享与共赢的目标。这不仅会导致内需的下降，也可能会影响到众多群体的幸福指数。您能否从博弈理论角度出发提出一个可行的共赢方案？
  问题5：目前外卖订单的配送距离约束相对较少且跨区域的配送较难实现，您能否设计出更长距离和跨区域的外卖订单的配送模式及其订单配送提成定价策略？

整体求解过程概述(摘要)

  外卖业务已经成为上班族生活中不可或缺的一部分。在数据分析驱动下，外卖骑手正在向更快更廉价的趋势发展。如何对外卖配送进行合理的定价和时长制定，对骑手设置奖惩措施，关系到外卖骑手以及平台、商家、消费者等多方利益。
  针对问题一，我们首先采用了模糊分析法对外卖配送服务的质量进行了评价标准制定。从两个目标同时出发运用模拟退火算法 TSP 制定出配送时长设计方案。借助平台调查数据与时长方案从平台与消费者双角度制定出针对骑手配送服务评价的奖惩措施。
  针对问题二，我们首先采用了层次分析法从问题一的奖惩函数扩展到更多因素如距离、工龄、高峰、天气以及顾客特殊需求等动静态因素影响。利用多元回归拟合多项式并改进效益函数对骑手满意度进行分析，最终对骑手的效用进行最大化，提出具有普遍适用性的配送费用提成定价和奖惩规则。
  针对问题三，我们首先采用了 dijkstra 算法模拟天气变化对路况的的影响进而计算得出规定的配送时长。然后我们引入哑变量模拟恶劣天气，利用多元函数对弹性时间
进行调整。创新研究空气质量对外卖订单数量，配送服务饱和率的影响，产生不同天气情况下骑手的配送费用和订单提成确定的策略。
  针对问题四，我们创新地借用了斯塔克尔伯格模型，对商家、骑手、平台、消费者四方抽象出效用函数，并且利用纳什均衡的思想以及多目标规划进行共赢满意度最大化求解，最终得到有关配送时长设定与提成定价的抽象策略描述。
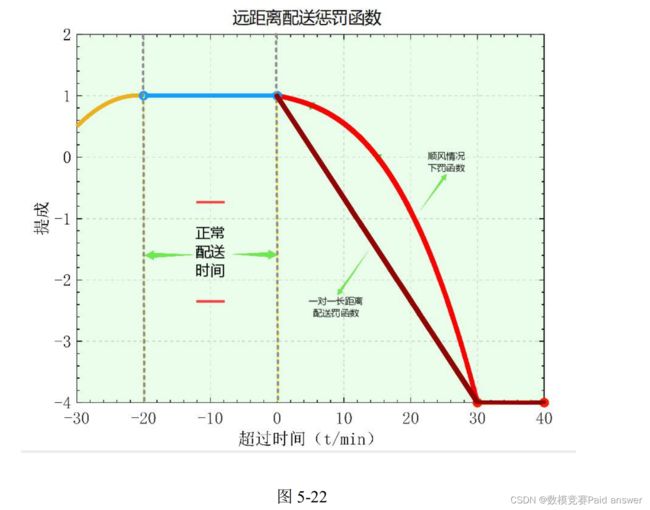
  针对问题五，我们首先设置骑手对远距离配送的敏感度函数并创新性地将服务分为专送与顺风送两种情况。然后采用聚类的思想并改进模拟退火算法为顺风派送进行时长设定，利用 dijkstra 算法形成最后针对远包配送两种服务的时长设计、提成定价以及奖惩策略。

问题分析：

  问题 1 属于综合评价类和对应策略类的抽象数学问题。希望通过对多因素赋予一定的权重制定合理的评价标准并且指定对应的解决方案。外卖的时间受到配送距离、外卖员的安全速度以及服务的完整有效性影响。外卖服务收到配送效率、配送礼仪和配送质量的影响，骑手安全主要受到行驶速度的影响。对于解决此类问题一般采用模糊分析法分析等先计算不同因素对研究对象的影响。同时，利用并改进模拟退火算法和 TSP 多元最优化算法设计骑手最优路线，据此设计平台预估配送时长。根据时长方案设计和多因素权重设计制定相应的来自平台与消费者双方的奖惩措施。
  问题二仍然属于综合评价类和对应策略的研究问题。与问题一相比，问题二将考虑更多的因素也更贴近现实情况，对骑手的福利与惩罚标准考量更多。订单提成定价的静动态因素和来自消费者的评分也间接影响多因素奖惩措施。静态因素有距离、是否专送等影响，动态因素有工龄，高峰期，天气，外卖质量，是否夜间外卖的影响。希望利用层次分析法给予各因素一定的权重，在对骑手的效用函数进行优化的过程中，通过因素对外卖提成定价和奖惩规则的影响进而影响满意度，最终达到效用最大化，得到关于提成定价与奖罚的一般规则。
  问题3属于评价策略类数学问题。对于解决此类问题一般采用优化处理如模拟退火、dijkstra 等方法进行路径优化和情景模拟。问题三的特点是主要专注于天气对外卖订单配送难度的增大以及骑手机会成本的提高，进而平台需要为骑手从配送时间的通融以及配送定价于奖励的提高进行相应的补偿，并进一步保证消费者的利益，实现多方共赢。另一方面，天气会影响外卖订单的数量和骑手的供给数量，在影响骑手机会成本的同时也产生服务供不应求的经济现象，在这种条件下服务的价格水平会有所提高，并反映在提成与奖励中。基于以上原因，我们首先对恶劣天气的道路情况建立模型进行路况模拟，进而对恶劣天气对外卖订单的供给与需求进行建模，从两方面对结果进行分析和预测，并得到时长与奖惩抽成的一般策略。
  问题四属于分析评价类问题，题目要求采用博弈论的思路进行解题。由于商家、骑手、平台、消费者的具体函数未知，故根据前三题中所做的假设进行合理化分析。当四方的效用函数相互制约达到纳什均衡时，相对应的提成定价函数和奖罚函数即为最优解。
此次博弈论分析由于平台作为规则的第一制定者，故采用斯塔克尔伯格模型分析四方的纳什均衡。
  问题五属于策略设计类问题，且题目中提出了一种新的配送模式，要求我们根据新模式的现实情况设置合理的配送模式。远距离配送需要考虑外部环境如距离、天气等多种出行成本以及内生问题如远包配送服务供给需求等对配送费的影响，同时骑手的配送
行为（专送与顺风）都会影响骑手的机会成本，同时平台的抽成与奖罚也会根据骑手的机会成本进行调整。同时，远包服务对骑手的综合素质要求更高，需要平台在所有骑手中进行一定的挑选，挑选标准需要根据此服务对骑手的要求进行设定。远包配送服务由骑手、消费者、平台三方相互制衡，三方相互挑选，给骑手更大的选择空间和更优厚的待遇。基于以上原因，我们首先建立一个针对骑手对长距离配送的敏感度函数，将之作为评判是否可以参与远包配送的条件之一。专送与顺风两种服务分别采用改进的模拟退火法和 dijkstra 算法进行时长设定，并根据现实调查进行奖惩与提成定价的设计。

模型假设：

  假设一：在不考虑其他因素影响的理想条件下，一个客户的订单只能由一辆车进行配送且不考虑配送员的个体差异性外卖骑手匀速直线运动，速度为 15km/h，且不受交通管制的影响。
  理由：理想状况下，仅考虑由距离决定从安全角度和服务质量出发的配送时长并根据美团技术平台要求，此假设符合条件。
  假设二：给予外卖骑手配送弹性时间为五分钟，最短送餐时间为五分钟。商家备餐时间为 20min。配送时间=备餐时间+送餐时间+弹性时间。
  理由：根据饿了么最新改进，考虑红绿灯、路况、天气以及电梯等突发情况，弹性时间设置合理。根据美团技术平台配送时间设计，该假设合理。
  假设三：城市道路为网格状，送餐员仅能沿正方形网格线行驶,且道路可双向行驶。
  理由：在考虑配送时长与最优路径时需考虑路段节点，网状结构符合中国道路形态与模型简化要求。
  假设四：假定当消费者下单时，商家与距离商家 15min 车程以内的所有骑手同时被告知，商家处理订单（此时备餐时间已经开始倒计时）；骑手有 5 分钟抢单时间，先到先得。忽略无人抢单的特殊情况。
  理由：从接单的现实性和人身安全以及商家制作流程完整性考虑，由现实的抢单策略理想化得来。
  假设五：消费者接受超过预期的快速配送
  理由：在骑手不违反交通规则的条件下，配送服务除了过快其他都是优质的，很少会有顾客投诉，美团外卖甚至没有对配送时间下限的设定。
  假设六：在长距离专向配送中，骑手行驶路线抽象为直线。
  理由：由 dijkstra 算法即可得到最短路线，无需考虑真实路线。
  假设七：远包顺风配送骑手到达店家时外卖已备好
  理由：远包配送距离与店家之间的距离有长度差，在假设消费者订单同时下达的条件下，店家将外卖已经备好的假设合理。
  假设八：在考虑目标条件的时候忽略一切其他外界因素的影响
  理由：现实中影响因素过多且在短时间内基本恒定，假设合理。

模型的建立与求解

模拟退火 TSP 模型的建立

  我们要解决的问题是在综合考虑外卖配送质量和骑手安全的情况下对外卖配送总时长进行合理规划，并对骑手服务制定合理的奖惩方法以提高外卖员的整体幸福水平和消费者满意度。题目要求我们综合考虑双方需要解决的问题是根据分析建模给出对骑手更加合理的时长和奖惩规定以防止过度剥削。从整体上看我们对现实中的时长规定放款了限制并增加了奖惩力度。相对宽松的时长规定能增强对骑手人身安全的保障，相对严格的奖惩制度可以提高优秀骑手的幸福水平并从骑手和商家两方面提高整体的外卖配送服务质量。
  （1） 具体研究过程：


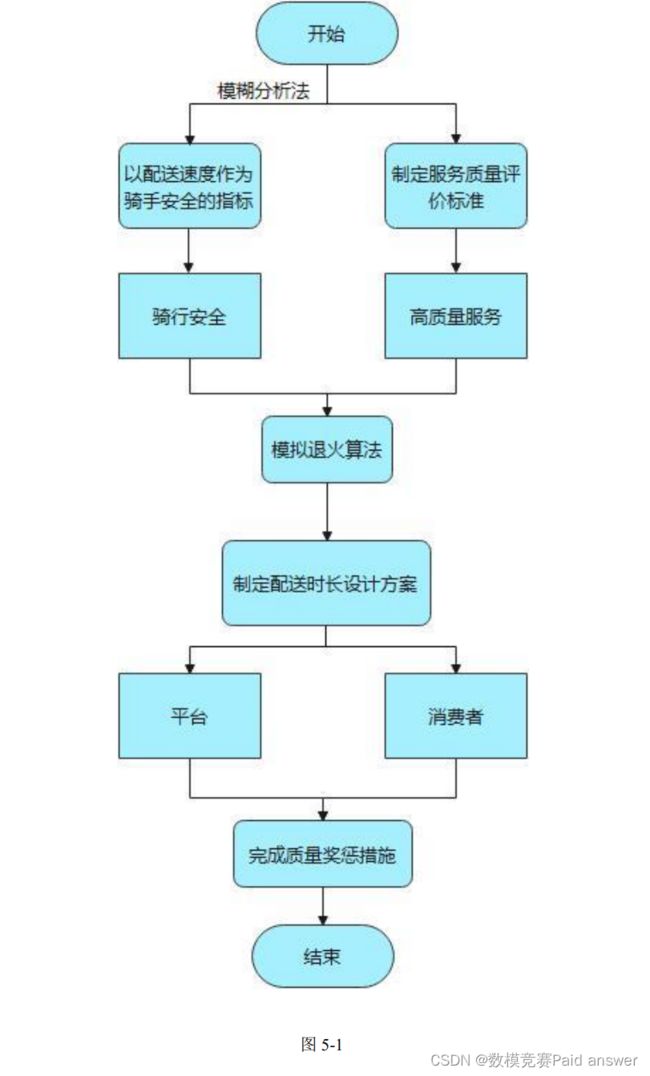
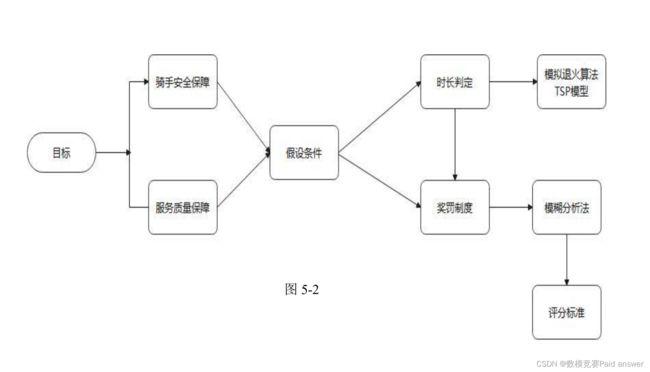
  研究过程优点：基于问题要求和最终目的提出适当的假设条件，针对不同的问题采用不同的研究方法，并将前后问题进行研究方法和结论的串通。
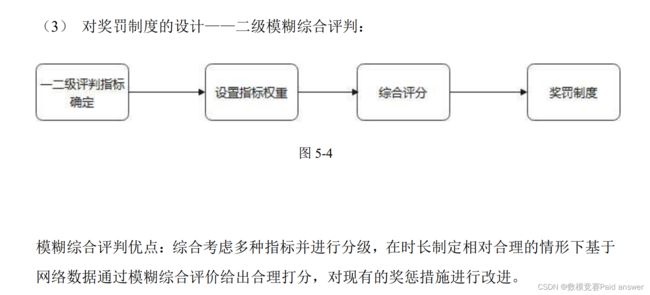
  （2） 对时长制定的设计——模拟退火法与 TSP 优化：
  模拟退火算法与 TSP 模型优点及创新之处：对配送时间进行合理的制定可以转化为最优路径问题。运用并从线路规划的角度改进模拟退火算法，建立无返回动态规划和最优路径选取，使之更加接近现实配送过程。对骑手接单的多种情况如：一对一、一对多与多对一等进行讨论，充分考虑最终目标与人性化设计，最终得到统一的评判指标。该算法有较强的局部搜索能力，程序运行时间短，且能保证最终结果逐步收敛于全局最优解，比较两种配送路线下的最优解，取最小值为本题的最终解。

模拟退火 TSP 模型与模糊综合评判模型的求解

  （1）模拟退火算法与 TSP 模型求解
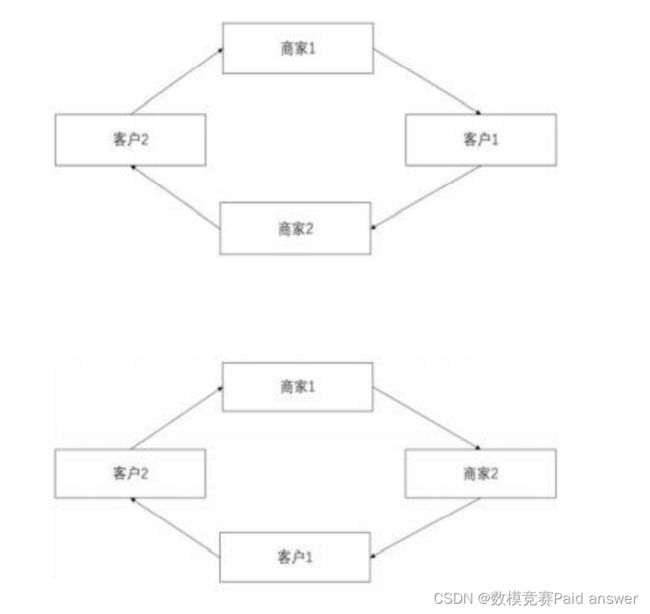
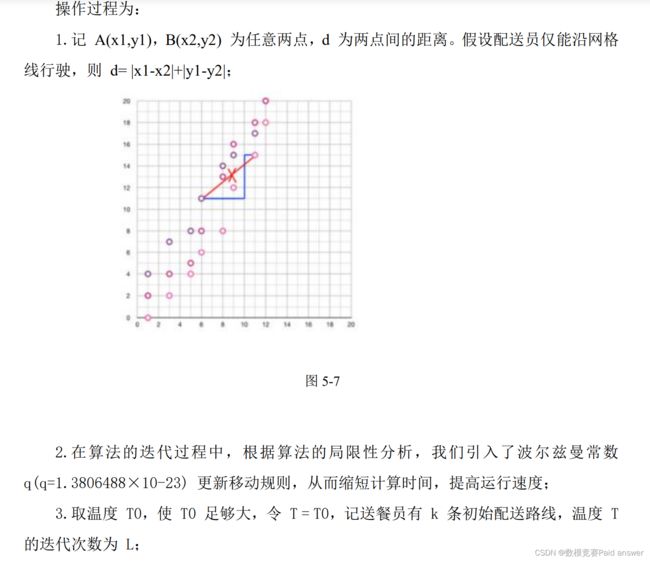
  制定合理的配送时间，可转化为最短路径(TSP)问题，使得在完成既定任务的情况下，实现送餐效率最高，送餐时间最短。进而对配送时间进行相应的调整。由于配送速度恒定，优化目标转化为求距离的最小值。考虑到摩托车承载能力的限制，将送餐员的配送路线分为如图 1、图 2 两种情况





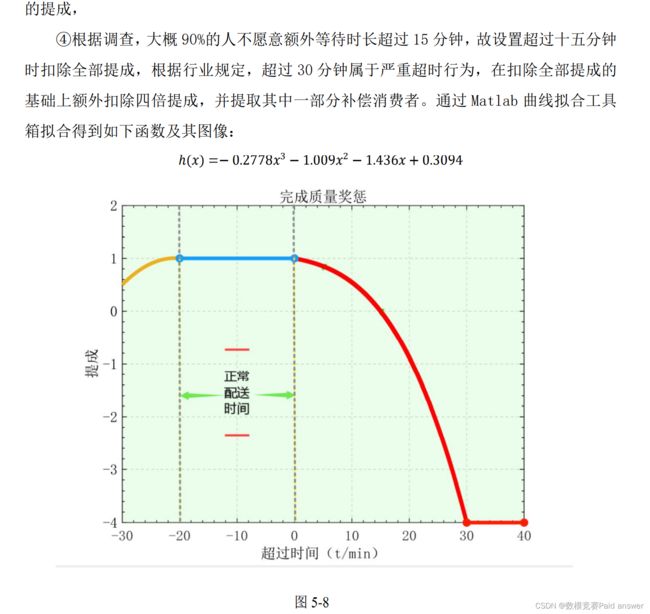
  3.基于模糊评判标准设定的消费者评价机制：
  ①根据消费者对配送服务的普遍要求调查，考虑以下评价因素：送餐时间、服务质量和送餐礼仪三个主要因素，并对主要因素进行二级分析。送餐时间综合考虑时间长短和骑手的人身安全，服务质量考虑外卖的完整性、准时性和冷热程度三方面，服务礼仪考虑电话礼仪和送餐礼仪两方面。如下图所示:




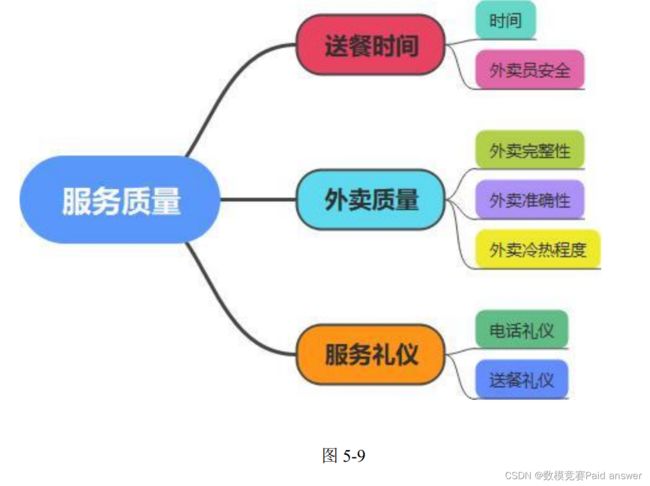
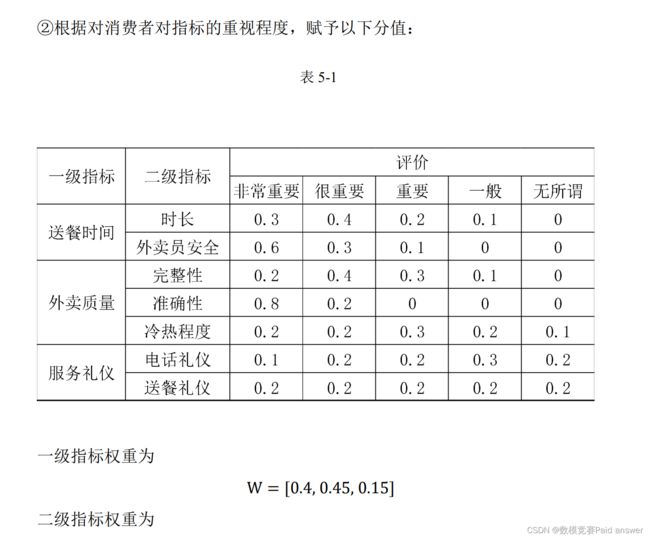
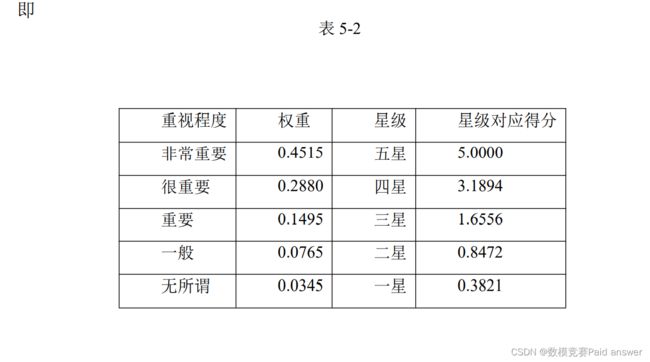
  假设不会恶意差评（客户没有不满意的情况下基本上是 4~5 星），客户分别对效率、质量和礼仪三个方面进行打分，相应星级得到分数乘以对应比重（效率：质量：礼仪=0.4:0.45:0.15），求和即为外卖员总得分。例如：客户对某外卖员打分情况为：效率五星，质量四星，礼仪三星，则该外卖员得分为：5×0.4+3.1894×0.45+1.6556×0.15=3.68357。
  4．奖惩措施制定
  将消费者评价奖惩设置四个阶段，外卖骑手每单得分 4.5 及以上可以获得由平台发放的配送费 20%的奖励；得分在 4.0 到 4.5 之间得到应得的抽成后的配送费；得分在3.0 到 4.0 之间时会被平台扣费，扣费函数为一次函数：留存收益（%）=（得分-3）*100%，直到扣完为止；得分在 2.0 到 3.0 之间时会被罚款，罚款函数为一次函数：罚款（%）= （-得分+3）*100%，直到罚款为配送费的一倍；得分在 2.0 以下时罚款为原配送费的一倍。
  基于对骑手安全和外卖配送质量双方面的考虑，通过模拟退火算法 TSP 路径优化对配送时间进行合理规划后得到恒定的最长要求配送时长。通过消费者对外卖服务打分和平台对配送准时的要求，设置相对灵活的奖惩措施，假设合理，模型具有一定的现实意义.

程序代码

A=[0.3 0.4 0.2 0.1 0
0.6 0.3 0.1 0 0
0.2 0.4 0.3 0.1 0
0.8 0.2 0 0 0
0.2 0.2 0.3 0.2 0.1
0.1 0.2 0.2 0.3 0.2
0.2 0.2 0.2 0.2 0.2]; %（模糊矩阵）
w=[0.4 0.45 0.15]; %（一级权重）
w1=[0.3 0.7]; %（二级权重）
w2=[0.4 0.5 0.1];
w3=[0.5 0.5];
b(1,:)=w1*A([1:2],:);
b(2,:)=w2*A([3:5],:);
b(3,:)=w3*A([6:7],:);
quanzhong=w*b
defen=5*quanzhong/quanzhong(1)

  我们要解决的问题是设定一个更加具有现实意义和普遍规律的奖惩方案和提成定价模式。题目要求是根据第一问的初步分析，加入静动态因素合成策略并考虑将骑手的效用最大化。具体步骤为以下几点：
  （1） 静动态因素对奖惩与定价的影响权重——层次分析法如图 1 所示，将问题分解为三个层次，最上层为目标层，即确定骑手各指标对提成重视程度；中间层为准则层，包括派送距离、骑手工龄、是否为高峰时期派送、天气等环境因素、派送物品完整度要求、是否在很少骑手工作的时段派送和派送质量；第三层为方案层，即预期 P1~P7

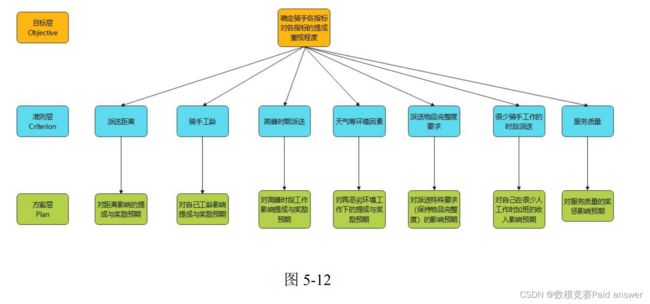
  定价提成策略

  奖罚策略
  1. 初步奖罚函数来源于第一题。
  2. 根据本题的层次分析加入多种静动态因素对奖罚函数进行修正
  3. 函数自变量有顾客评分、派送距离、骑手工龄等连续性变量以及是否高峰期、是否恶劣天气、是否夜间配送等二元变量。
  4. 奖励来源于所有因素，惩罚只来源于顾客评分。
  5. 多种奖励单独计算。
  6. 派送距离奖励制度为超出五公里的情况下，每单每超出三公里奖励原配送费的 20%。
  7. 骑手工龄的奖励制度为工作时间超出两年的情况下，每单奖励原配送费的 5%*超额工龄。
  8. 高峰期派送在原派送费的 90%的基础上抽成，也就是骑手在不受到惩罚的情况下保底有百分之十的配送费。
  9. 恶劣天气派送在原派送费的 80%的基础上抽成，也就是骑手在不受到惩罚的情况下保底有百分之二十的配送费。
  10. 夜间配送在原配送费的 90%的基础上抽成，也就是骑手在不受到惩罚的情况下保底有百分之二十的配送费。
  11. 加权平均为骑手的最终佣金，在所有条件均存在的情况下权重为
  评价：0.1375
  距离：0.0471
  工龄：0.3745
  天气：0.1440
  夜间配送：0.2132
  高峰配送：0.0837
  若有条件不满足，则仅考虑存在的因素并等比例放大至和为1

层次分析模型的求解

  构造矩阵 M，将准则层中七个因素两两比较，如果 C1 项与 C2 项同样重要，则标度为 1；若 C1 比 C2 稍微重要，则标度为 2；若 C1 比 C2 明显重要，则标度为 5；若 C1 比C2 强烈重要，则标度为 7；如果 C1 和 C2 相比标度为 4，那么 C2 和 C1 相比就是 1/4。根据此准则得比较矩阵：


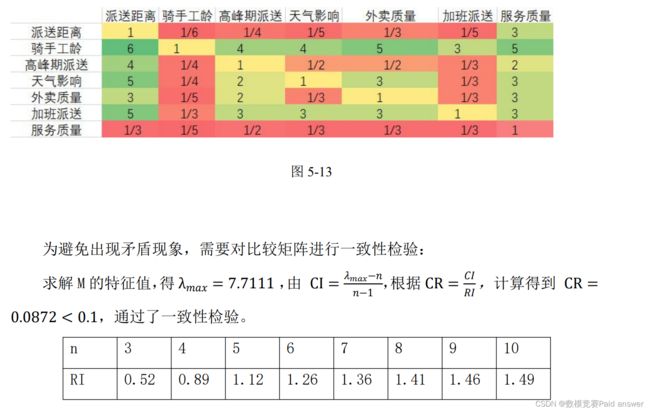
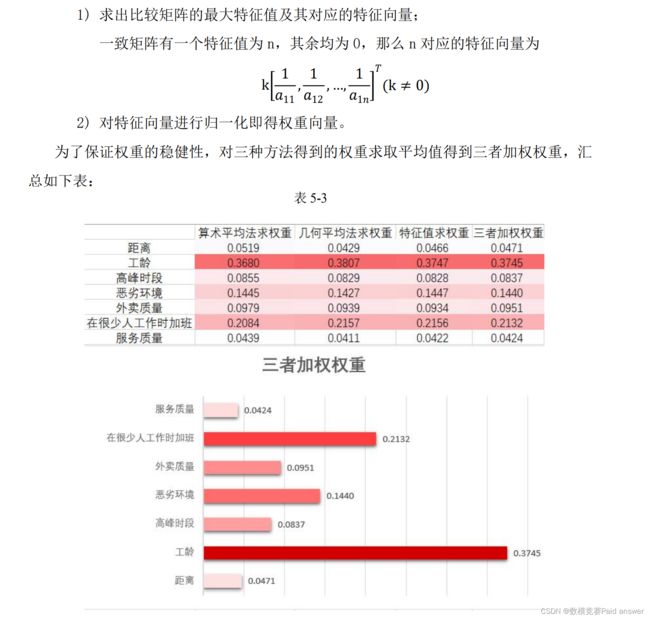
  影响骑手最终佣金的主要有规则提成定价和奖罚制度且奖罚制度重综合考虑了提成定价。根据分析，我们发现利用层次分析法确定的各权重相对符合实际，且考虑到多种情况。
  （1） 骑手的配送服务为最重要的衡量指标，但是他是最基本的且其他因素出现的频率较低，故在权重赋予的时候有所保留。
  （2） 骑手工龄也严重影响其工资水平，以期骑手能稳定在一个平台工作。
  （3） 天气、路况和夜间配送主要考虑的是对骑手出行安全和服务质量的保证，在可能出现差评或者投诉的情况下适当进行弥补。
  （4） 根据初步分析，发现该奖罚措施的惩罚仅局限在消费者的评价，面对其他的条件，实惠让骑手的薪资水平上升，假设骑手的满意度随着薪资水平的上升而上升且不考虑其他因素的条件下，该策略有利于骑手的效益最大，最后在能够达到满意度最大的条件。

多元线性回归模型的建立

  我们需要解决的问题是天气状况对外卖配送定价与时长设计的影响。题目要求我们考虑各种恶劣环境得到普适性规律。模型建立分为以下两步：
  （1） 天气对外卖配送服务饱和度的影响——外卖服务需求方角度配送服务饱和度的定义为当前配送服务的需求量对当前骑手所能承受的最大销量的比率。为检验外卖销量即外卖服务需求量与天气变量的关系，采用多元回归分析，建立如下模型：

  经过分析，我么得到如下结论。天气的不舒适度对外卖的销售存在正相关关系，当炎热或寒冷等不适天气状况下，人们会倾向于增大订购外卖的力度，外卖销量上升的同时外卖配送服务的需求也会上升。同样的，降雨天气同也带动销量增长，并且随着雨势增大，相关系数变大，外卖需求量的增长幅度也越来越大。



  （2） 天气对骑手配送难度的增加——配送服务供给方角度
  天气作用在交通速度和道路安全情况上，晴朗时交通通畅，路况好，出行较为安全；而恶劣天气对路况造成不良影响，车辆行进速度受到阻碍，出现道路拥堵现象，同时还会提高交通事故的发生概率。外卖服务需要保证食物味道的鲜美，要求有高效的配送效率。当天气状况恶劣时，送餐速度会受到交通状况的影响，而顾客对外卖的送餐速度关注较大，配送超时、饭菜变凉等问题都可能导致顾客对本次用餐的不满，并可能会进行负面评价，进而影响下次的订餐选择和其他消费者对该商家的选择。我们充分利用 dijkstra 等方法进行路径优化和情景模拟，对恶劣天气情况将会对配送时间造成的影响进行分析，并得到一定的结论

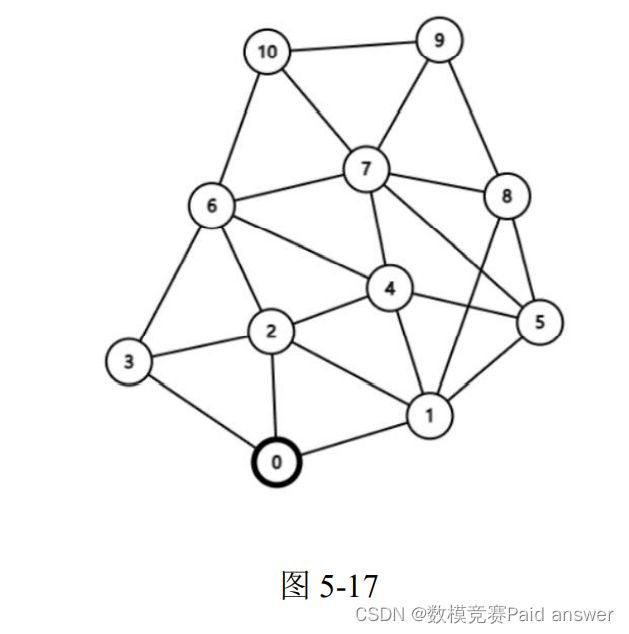
  图示为 diskstra 算法的基本思路。“0”为骑手的初始位置，二到十为骑手的目标位置，包括商家与消费者所在区域。骑手需沿设计好的路线进行最优路线选择。恶劣天气会毁坏其中的一个或几个道路节点，使得整个路途瘫痪，需绕开重新寻找最优路径。

多元线性回归模型的求解

  （1） 多元线性回归模型的结论：
  1. 天气的不舒适程度与外卖的销量正相关。无论是严寒还是酷暑，都会增加外卖的销量。天气舒适度是对温度和湿度的综合计算，反映的是人们对这两个指标的身体感受。
  2. 降雨天气会增加出行的困难度，从而增加外卖的销量和外卖服务的需求量。并且随着降雨量的增大，外卖需求的数量和增速都会增大。但是这种增长是有上限的。降雨等级越大，对外卖配送的阻碍也会越来越大。当阻碍达到一定程度时，外卖的配送时间超出人们的预期，外卖品质下降，外卖的订单销量可能就不会继续增长。
  3. 降雪天气对在线外卖平台的销量没有显著的影响，降雪可能触发了人们订购外卖的需求，但是在雪天环境可能对外卖的配送造成了阻碍，并没有实现平台订单量的显著变化。
  4. 空气质量对外卖平台销量的影响与地区有关，不同的地区的用户群体对空气质量的关注有差异。目前缺乏空气质量与消费行为间关系的研究，本文创新性的将空气质量情境与在线外卖平台的销量联系在一起，给情境效应与消费行为的研究增添了新的视角。

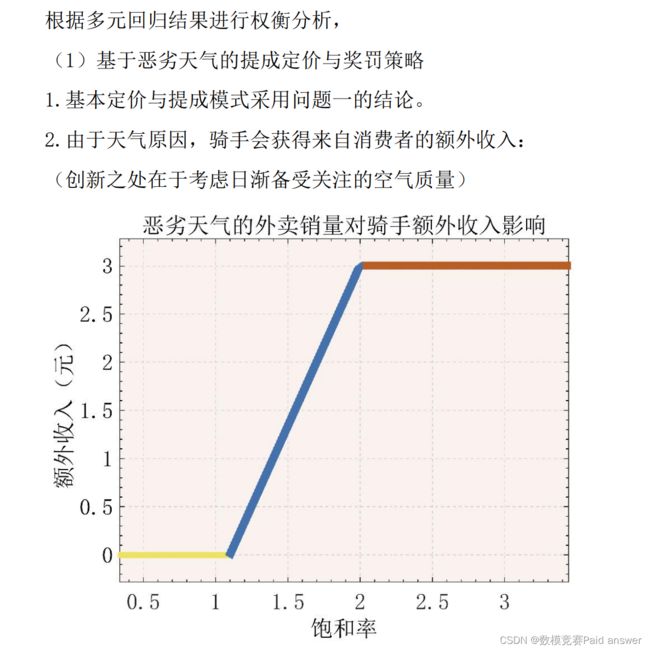
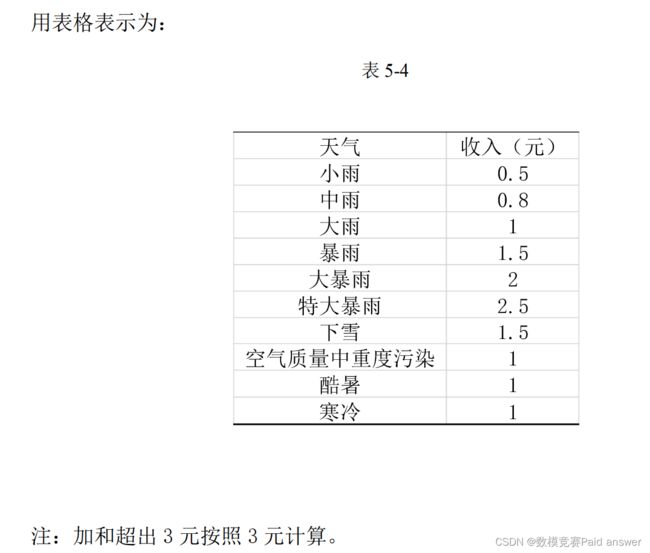
斯塔尔伯格博弈模型的建立

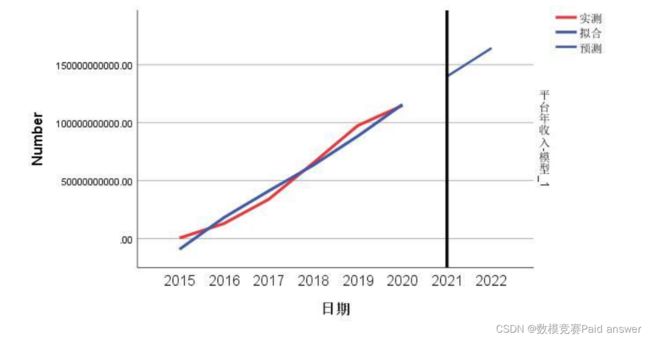
  我们需要解决的问题是从博弈论的角度出发，考虑内需扩大，提出能实现商家、骑手、平台、消费者四方共赢的策略。从可观察的收入数据来看，商家、骑手、平台的营销收益普遍存在一种长期递增的趋势。

斯塔尔伯格博弈模型的求解

  经过分析计算，我们发现配送价格与骑手的收益有不确定关系，分别从外卖订单数和单位订单的可获利润双方影响；配送时长对骑手的收益有不确定性关系，分别从消费者的需求量和骑手的每日接单数两方面影响；奖惩方案一定程度上可以提高优质骑手的福利水平，同时对平台的影响是不确定的，分别从成本和客户流量双方面影响。
  针对上述分析，提出以下策略：
  2 骑手与消费者的制衡：
  骑手与消费者双向评价，实行抽成浮动制。单位配送费不再单方面取决于骑手的服务质量，还取决于消费者是否存在恶意差评的行为。
  3 骑手与商家的制衡：
  商家可能存在延长备餐时间恶意缩短骑手送餐时间的行为。骑手对商家进行打分。分数影响到商家入驻平台的固定成本。
  4 骑手与平台的制衡：
  合理的奖惩制度和时长与提成设计方案可以实现此制衡。
  5 平台与消费者的制衡：
  消费者可能存在恶意投诉索取赔偿的行为，平台对消费者的近期行为进行打分评判，配送费依据分数浮动。
  6 平台与商家的制衡：
  商家选择不同的平台进行成本的比较，同时平台还可以根据商家信誉给予一定的优惠政策。
  7 霍尔特模型收益预测：

聚类算法的应用与 TSP 模型的建立与求解

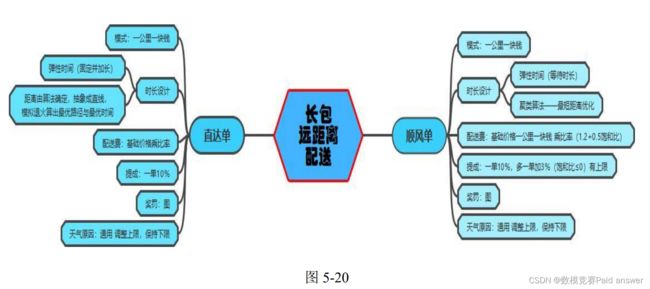
  我们需要解决的问题是针对远包派送这一种特殊的服务模式给出完整的从配送定价、提成到对骑手的奖罚的策略以提高骑手的生活水平，并激励他们把工作做好。具体步骤如下：

（1） 骑手敏感度函数的建立：

  （2） 基于聚类算法的顺风单的最短距离模型

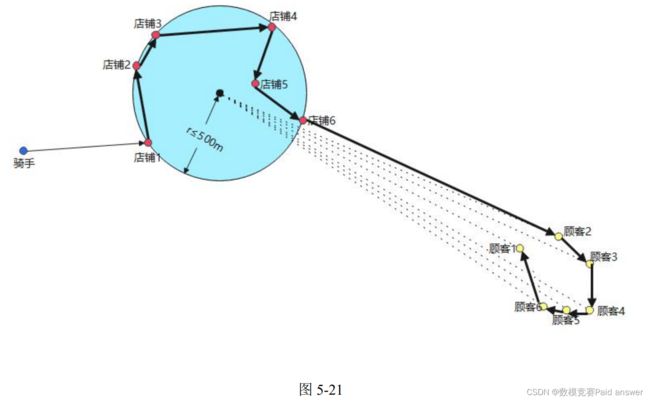
  基本思路为：顺风骑手一次从一地出发去往多个店铺取餐并最终到达多地送餐，假设骑手到达所有商家时可以立即取餐且配送时弹性时间的压缩无累积效应，经过聚类算法将可选的所有店铺的点用一个最小圆包围，条件为半径小于 500m。因为存在五千米与五百米的距离差，在考虑消费者所在区域时采用如下思路：将店铺所对应的消费者所在位置与所有店铺的最小圆的圆心的连线中所成最大的夹角小于 45 度时顾客可以选择是否选用顺风服务。
  （3） 基于模拟退火法与 dijkstra 算法的专送最优路线模型远距离专送即为众包的一对一模式，仅需要考虑外界环境如道路形态、路况等对骑手路线的影响。采用模拟退火法与 dijkstra 算法可以将骑手的最优行驶路线在一定的外界条件重模拟出并找到最优路线。基于最优路线设定基本配送时长。由于距离较远且算法已经给出最优路线，则骑手的具体行程可以抽象为直线。
  （4） 远包配送服务的奖罚函数模型远包配送服务的奖惩分为专送与顺风两种策略。顺风模式与短距离类似，经 Matlab软件拟合即可得到与问题一相似的策略函数；专门配送考虑到骑手的主观能动性和平台的优惠政策，对错误的容忍度更小，故曲度更小，考虑现实情况，采取一次函数模式。

结果

  （1）对骑手进行远包配送服务的挑选规则为优化产品服务，并提高优质骑手的薪资待遇，制定以下平台对骑手的选择策略。
  1 为保证服务质量，需选用消费者综合评分 4.0 以上的骑手。
  2 为保证骑手的人身安全维护道路交通建设，需选用罚单率以及投诉率小于 10%的骑手。
  3 从尊重骑手的配送习惯与选择并适当鼓励远包配送服务的发展的角度考虑，需选取敏感度函数小于阙值的骑手。敏感度越小反映骑手越不反感远程配送，则可以增加此种服务的提供数量。具体规则为：将骑手的敏感度进行排序，取最小值的 40%内的人可以接长单，越小越容易接到长单
  4 平台对长单的基本抽成减少 3%。
  5 服务分为两种类型，专送与顺风，具体由消费者挑选。
  （2）时长设计
  针对两种不同的服务模式，分别采取不同的时长设计方式。
  1 两种模式备餐时间均沿用为 15min
  2 对顺风单的弹性时间不作改变；对专送服务考虑到路线规划要求以及红绿灯问题延长 3min。
  3 对顺风单的送餐时间设计采用聚类算法进行路径优化，继续沿用 15km/h 的骑行速度计算得到送餐时间
  （3）基础配送费设计
  根据网上调查，日常生活中的配送费为 3km 给予 2.0 元提成，计算得到对于长距离配送 1 元/千米较为合理。
  1 顺风单的基础配送费为 1 元/千米与补贴系数的成绩，系数为（1.2+0.5*σ）。
  2 专送服务的基础配送费为 1 元/千米与补贴系数的乘积，系数为（1.0+σ）
  （4）抽成设计
  1 专送服务与普通配送抽成相同为 10%。
  2 顺风服务考虑骑手机会成本递减效应，平台将加大抽成力度，基础抽成为 10%，每多加一单抽成增加 3%，抽成上限为 25%。
  （5）天气补贴
  天气补贴通过调整上下限来体现。基于第三问，抽成下限降为 5%。
  （6）奖罚策略
  奖罚仍然基于超时状态，顺风模式与短距离类似，经 Matlab 软件拟合即可得到与问题一相似的策略函数；专门配送考虑到骑手的主观能动性和平台的优惠政策，对错误的容忍度更小，故曲度更小，考虑现实情况，采取一次函数模式。

论文缩略图：

程序代码：

A =[ 1.0000 0.1667 0.2500 0.2000 0.3333 0.2000 3.0000
6.0000 1.0000 4.0000 4.0000 5.0000 3.0000 5.0000
4.0000 0.2500 1.0000 0.5000 0.5000 0.3333 2.0000
5.0000 0.2500 2.0000 1.0000 3.0000 0.3333 3.0000
3.0000 0.2000 2.0000 0.3333 1.0000 0.3333 3.0000
5.0000 0.3333 3.0000 3.0000 3.0000 1.0000 3.0000
0.3333 0.2000 0.5000 0.3333 0.3333 0.3333 1.0000]; %一致矩阵
[n,n] = size(A);
% 算术平均法
Sum_A = sum(A);
SUM_A = repmat(Sum_A,n,1);
Stand_A = A ./ SUM_A;
%几何平均法
Prduct_A = prod(A,2);
Prduct_n_A = Prduct_A .^ (1/n);
%特征值法
[V,D] = eig(A);
Max_eig = max(max(D));
[r,c]=find(D == Max_eig , 1);
%计算一致性比例 CR 的环节
CI = (Max_eig - n) / (n-1);
CR=CI/1.36
%%ri 对应 1.3.6
%%三个权重取均值保证稳健性！！
cengcifenxifaquanzhong=(sum(Stand_A,2)./n+Prduct_n_A ./ sum(Prduct_n_A)+V(:,c) ./ sum(V(:,c)))/3