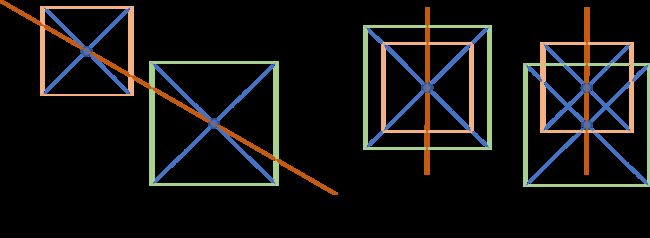AK F.*ing leetcode 流浪计划之线段求交
欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
本期话题:2条线段求交点
我有两种线段求交方法。 这两种方法在图形中窗口剪裁中应用。
分别是 Cohen-Suther land算法和Liang-Barsky裁剪算法。
两种方法都是解方程第一种是点斜式方程,第二种是参数化方程。
在leetcode几何专题中也有几道线段求交的题。
符号定义: * 是向量点乘或普通数相乘,X代表向量叉积。
注意点:浮点型判断大小只能近似判断
点斜式方程法
简单来讲就是两条直线方程,解出两个未知数x,y。
已知两条线段 P0P1, P2P3
其 中 坐 标 P 0 ( x 0 , y 0 ) , P 1 ( x 1 , y 1 ) , P 2 ( x 2 , y 2 ) , P 3 ( x 3 , y 3 ) 其中坐标P_0(x_0,y_0), P_1(x_1,y_1),P_2(x_2,y_2),P_3(x_3,y_3) 其中坐标P0(x0,y0),P1(x1,y1),P2(x2,y2),P3(x3,y3)
利用点斜式表示法,设两条直线为
m 1 = ( y 1 − y 0 ) / ( x 1 − x 0 ) m_1 = (y_1-y_0)/(x_1-x_0) m1=(y1−y0)/(x1−x0)
y = y 0 + ( x − x 0 ) ∗ m 1 y=y_0+(x-x_0)*m_1 y=y0+(x−x0)∗m1
m 2 = ( y 3 − y 2 ) / ( x 3 − x 2 ) m_2 = (y_3-y_2)/(x_3-x_2) m2=(y3−y2)/(x3−x2)
y = y 2 + ( x − x 2 ) ∗ m 2 y=y_2+(x-x_2)*m_2 y=y2+(x−x2)∗m2
消除y得到:
y 0 + ( x − x 0 ) ∗ m 1 = y 2 + ( x − x 2 ) ∗ m 2 y0+(x-x0)*m1 = y2+(x-x2)*m2 y0+(x−x0)∗m1=y2+(x−x2)∗m2
移项,合并同类项,解出x
x = ( y 0 − y 2 − x 0 ∗ m 1 + x 2 ∗ m 2 ) / ( m 2 − m 1 ) x = (y0-y2-x0*m1+x2*m2) / (m2-m1) x=(y0−y2−x0∗m1+x2∗m2)/(m2−m1)
再任选择一条直线解出y:
y = y 0 + ( x − x 0 ) ∗ m 1 y=y_0+(x-x_0)*m_1 y=y0+(x−x0)∗m1
优化及特殊情况
1. 提前判断有没有交点
上述过程是求解两条直线的交点,实际求出交点可能不在线段中。
所以可以通过向量的叉积提前判断两条线段的关系。
具体方法如下 详细方法参考这个链接 线段判交
跨立测试
![]()
只要计算向量 (P1-P3)*(P4-P3), (P1-P3)*(P2-P3), 判断它们是不是异号,即可知道P4, P2 是不是在线段P1P3的2侧。对线段P2P4也做同样的测试。
该方法只涉及到整数计算。
2. 共线情况
此时,有可能两条线段没有集,需要先判断。
如果有交集,它们是一条线段,而不是一个点。

除了以上情况外,剩下就是有交点,但还有两种特殊情况。
3. 有一条线段垂直于X轴
此时,斜率是无穷大,不能用上述式子去解x。
可以直接用x代入另一条方程解得y。
4. 有一条线段垂直于Y轴
同理,可以代入另一条方程求得x。
实现
参考题目:https://leetcode-cn.com/problems/intersection-lcci/
题目大意要求2条线段的交点,如果没有交点输出空。
如果共线有交,则输出交集最左下角的坐标。如果x轴相同就输出y小的坐标。
AC代码
package main
import (
"fmt"
"math"
)
var esp float64 = 1e-6
// 比较浮点型:0 相等,1 >, -1 <
func cmpDouble(a, b float64) int {
if math.Abs(a-b) < esp {
return 0
}
if a < b {
return -1
}
return 1
}
func xmult(p1, p2 []int) int {
return p1[0]*p2[1] - p1[1]*p2[0]
}
// 0 无交点,1 有交点,2 共线
func lineStatus(start1 []int, end1 []int, start2 []int, end2 []int) int {
// 跨立测试
m1 := xmult([]int{end1[0] - start1[0], end1[1] - start1[1]}, []int{start2[0] - start1[0], start2[1] - start1[1]})
m2 := xmult([]int{end1[0] - start1[0], end1[1] - start1[1]}, []int{end2[0] - start1[0], end2[1] - start1[1]})
if m1 == 0 && m2 == 0 {
return 2
}
m3 := xmult([]int{end2[0] - start2[0], end2[1] - start2[1]}, []int{end1[0] - start2[0], end1[1] - start2[1]})
m4 := xmult([]int{end2[0] - start2[0], end2[1] - start2[1]}, []int{start1[0] - start2[0], start1[1] - start2[1]})
if m1*m2 > 0 || m3*m4 > 0 {
return 0
}
return 1
}
// 获取共线重合最左下坐标
func getOneLine(start1 []int, end1 []int, start2 []int, end2 []int) []float64 {
start := start1
end := end1
if start1[0] == end1[0] {
// 比较Y轴
if start2[1] > start[1] {
start = start2
}
if end2[1] < end[1] {
end = end2
}
// 没有重叠部分
if start[1] > end[1] {
return []float64{}
}
return []float64{float64(start[0]), float64(start[1])}
}
// 比较 X轴
if start2[0] > start[0] {
start = start2
}
if end2[0] < end[0] {
end = end2
}
// 没有重叠部分
if start[0] > end[0] {
return []float64{}
}
return []float64{float64(start[0]), float64(start[1])}
}
// 已知x值求解Y (线段不平行于Y轴)
// y = start[1] + (x-start[0])*(end[1]-start[1])/(end[0]-start[0])
func getYWithX(x float64, start, end []int) []float64 {
if start[0] > end[0] {
return getYWithX(x, end, start)
}
y := float64(start[1]) + (x-float64(start[0]))*float64(end[1]-start[1])/float64(end[0]-start[0])
return []float64{x, y}
}
// 已知Y值求解X (线段不平行于X轴)
// x = start[0] + (y-start[1])*(end[0]-start[0])/(end[1]-start[1])
func getXWithY(y float64, start, end []int) []float64 {
if start[1] > end[1] {
return getXWithY(y, end, start)
}
x := float64(start[0]) + (y-float64(start[1]))*float64(end[0]-start[0])/float64(end[1]-start[1])
return []float64{x, y}
}
func intersection(start1 []int, end1 []int, start2 []int, end2 []int) []float64 {
// 左右坐标统一化。
// x 小的放在前
if start1[0] > end1[0] || (start1[0] == end1[0] && start1[1] > end1[1]) {
return intersection(end1, start1, start2, end2)
}
if start2[0] > end2[0] || (start2[0] == end2[0] && start2[1] > end2[1]) {
return intersection(start1, end1, end2, start2)
}
// 判断是否共线
ls := lineStatus(start1, end1, start2, end2)
if ls == 0 {
return []float64{}
}
if ls == 2 {
return getOneLine(start1, end1, start2, end2)
}
// 判断有直线垂直于x轴
if start1[0] == end1[0] {
return getYWithX(float64(start1[0]), start2, end2)
}
if start2[0] == end2[0] {
return getYWithX(float64(start2[0]), start1, end1)
}
// 判断有直线垂直于Y轴
if start1[1] == end1[1] {
return getXWithY(float64(start1[1]), start2, end2)
}
if start2[1] == end2[1] {
return getXWithY(float64(start2[1]), start1, end1)
}
// 普通情况
/* 先求出交点x
m1 = (y1-y0)/(x1-x0)
y=y0+(x-x0)*m1
m2 = (y3-y2)/(x3-x2)
y=y2+(x-x2)*m2
y0+(x-x0)*m1 = y2+(x-x2)*m2
x = (y0-y2-x0*m1+x2*m2) / (m2-m1)
*/
m1 := float64(end1[1]-start1[1]) / float64(end1[0]-start1[0])
m2 := float64(end2[1]-start2[1]) / float64(end2[0]-start2[0])
x := (float64(start1[1]-start2[1]) - float64(start1[0])*m1 + float64(start2[0])*m2) / (m2 - m1)
// 求出y
return getYWithX(x, start1, end1)
}
func intersectionArr(arr []int) []float64 {
return intersection(arr[0:2], arr[2:4], arr[4:6], arr[6:8])
}
/*
func main() {
fmt.Println(intersectionArr([]int{0, 0, 1, 0, 1, 1, 0, -1}))
fmt.Println(intersectionArr([]int{0, 0, 3, 3, 1, 1, 2, 2}))
fmt.Println(intersectionArr([]int{0, 0, 1, 1, 1, 0, 2, 1}))
fmt.Println(intersectionArr([]int{0, 0, 10, 0, 10, 0, 11, 0}))
fmt.Println(intersectionArr([]int{10, 0, 0, 0, -10, 0, -11, 0}))
fmt.Println(intersectionArr([]int{0, 10, 0, 20, 1, -1, -1, 1}))
fmt.Println(intersectionArr([]int{0, 10, 0, 0, 1, -1, -1, 1}))
fmt.Println(intersectionArr([]int{10, 0, -10, 0, 11, -1, -1, 1}))
fmt.Println(intersectionArr([]int{10, -10, -10, 10, 10, -10, -10, 10}))
fmt.Println(intersectionArr([]int{10, -10, -10, 10, -10, -10, 10, 10}))
fmt.Println(intersectionArr([]int{1000, -1123, -1123, 1333, -1000, -1000, 1000, 1000}))
fmt.Println(intersectionArr([]int{1000, 0, 2000, 0, 1000, 1, 2000, 1}))
fmt.Println(intersectionArr([]int{1000, 123, 2000, -123, 1000, 1, 2000, -123}))
fmt.Println(intersectionArr([]int{1000, 123, 2000, -123, 1000, 1, 2000, -123}))
fmt.Println(intersectionArr([]int{1000, 0, 2000, 0, 2000, 0, 2000, 1}))
}
*/
参数化法
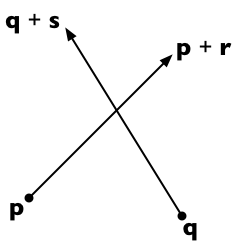
如图,s, r 分别是两条线段起点指向终点的向量。
可利用参数方程表示法
点p 到 p+r 表示线段1
点q 到 q+s 表示线段2
用参数化表示
线段1 上1点用 p’ = p+t*r (0<=t<=1)
线段2 上1点用 q’ = q+u*s (0<=u<=1)

对线段求交就是让两式相等。
p+t*r= q+u*s
让两边都叉积以s
(p+t*r) X s = (q+u*s) X s
由于s X s ==0
可以得到
p X s + t*r X s = q X s
t = (q-p) X s /(r X s)
同理两边叉乘以r求出u,根据 r X s = - s X r
u = (p-q) X r / (s X r) => u = (q-p) X r / (r X s)
以下分4种情况讨论
1. 两条线段共线。
此时,r X s = 0 && (p-q) X r == 0。
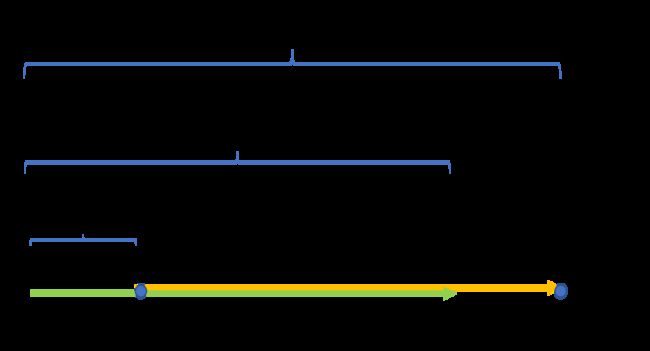
如图,计算 (q-p)在r上的投影在r长度上的占比t0,
计算(q+s-p)在r上的投影在r长度上的占比t1,查看[t0, t1]是否与范围[0,1]有交集。如果t0>t1, 则比较[t1, t0]是否与范围[0,1]有交集。
计算投影可以根据点乘公式, 计算
a· b = |a|· |b|· cos∂, 此时∂=0,所以cos∂ = 1
投影就是b的长度 a*b / |a|, 这个是带方向的。
t0 是 (q-p)在r上的投影在r长度上的占比。
就是分别计算 (q-p)在r,r在r上的投影,然后比一下就可以。
t0 = (q-p)*r/(r*r) ,由于投影是有方向的,如果q点在p点的左方,计算出来是负数,自然也就是在r的外面。
同理,求出t1。
t1 = (q+s-p)*r/(r*r) = t0 + s · r / (r · r)
2. 两条线段平行。
此时,r X s = 0 && (p-q) X r != 0。没有交点。
3. 不平行但有交点。
此时,按照
t = (q-p) X s /(r X s)
u = (q-p) X r / (r X s)
求出t,u, 并判断 0<=t<=1 && 0<=u<=1。
3. 不平行但有交点。
此时,求出t,u, 并判断t 或 u 不在[0,1]范围。
实现
参考题目:https://leetcode-cn.com/problems/intersection-lcci/
题目大意要求2条线段的交点,如果没有交点输出空。
如果共线有交,则输出交集最左下角的坐标。如果x轴相同就输出y小的坐标。
AC代码
package main
import (
"fmt"
"math"
)
var esp float64 = 1e-6
// 比较浮点型:0 相等,1 >, -1 <
func cmpDouble(a, b float64) int {
if math.Abs(a-b) < esp {
return 0
}
if a < b {
return -1
}
return 1
}
func xmult(p1, p2 []int) int {
return p1[0]*p2[1] - p1[1]*p2[0]
}
// 点积
func dotProduct(a, b []int) float64 {
return float64(a[0]*b[0] + a[1]*b[1])
}
func getPoint(p, r []int, t float64) []float64 {
p0 := float64(p[0]) + t*float64(r[0])
p1 := float64(p[1]) + t*float64(r[1])
return []float64{p0, p1}
}
// 共线求解交点
// t0 = (q-p)*r/(r*r)
// t1 = (q+s-p)*r/(r*r) = t0 + s · r / (r · r)
func getOnlinePoint(q []int, s []int, p []int, r []int) []float64 {
t0 := dotProduct([]int{q[0] - p[0], q[1] - p[1]}, r) / dotProduct(r, r)
t1 := t0 + dotProduct(s, r)/dotProduct(r, r)
if cmpDouble(t0, t1) > 0 {
t0, t1 = t1, t0
}
// 没有交集
if t1 < 0 || t0 > 1 {
return []float64{}
}
// 与 [0, 1]区间求交集
t0 = math.Max(0, t0)
t1 = math.Min(1, t1)
// 求解起终点
p0 := getPoint(p, r, t0)
p1 := getPoint(p, r, t1)
// 查看x轴小的先返回
if cmpDouble(p1[0], p0[0]) < 0 {
p0 = p1
} else if cmpDouble(p1[0], p0[0]) == 0 && cmpDouble(p1[1], p0[0]) < 0 { // x 轴相同比较y轴
p0 = p1
}
return p0
}
func isInRange01(t float64) bool {
if t < 0 || t > 1 {
return false
}
return true
}
/*
点p 到 p+r 表示线段1
点q 到 q+s 表示线段2
线段1 上1点用 p' = p+t*r (0<=t<=1)
线段2 上1点用 q' = q+u*s (0<=u<=1)
让两式相等求交点 p+t*r = q+u*s
两边都叉乘s
(p+t*r)Xs = (q+u*s)Xs
pXs + t*rXs = qXs
t = (q-p)Xs/(rXs)
同理,
u = (p-q)Xr/(sXr) -> u = (q-p)Xr/(rXs)
以下分4种情况:
1. 共线,sXr==0 && (q-p)Xr==0, 计算 (q-p)在r上的投影在r长度上的占比t0,
计算(q+s-p)在r上的投影在r长度上的占比t1,查看[t0, t1]是否与范围[0,1]有交集。
如果t0>t1, 则比较[t1, t0]是否与范围[0,1]有交集。
t0 = (q-p)*r/(r*r)
t1 = (q+s-p)*r/(r*r) = t0 + s · r / (r · r)
2. 平行sXr==0 && (q-p)Xr!=0
3. 0<=u<=1 && 0<=t<=1 有交点
4. 其他u, t不在0到范围内,没有交点。
*/
func intersection(q []int, end1 []int, p []int, end2 []int) []float64 {
s := []int{end1[0] - q[0], end1[1] - q[1]}
r := []int{end2[0] - p[0], end2[1] - p[1]}
// 计算 (q-p)Xr
qpr := xmult([]int{q[0] - p[0], q[1] - p[1]}, r)
if xmult(s, r) == 0 {
if qpr != 0 {
return []float64{}
}
return getOnlinePoint(q, s, p, r)
}
qps := xmult([]int{q[0] - p[0], q[1] - p[1]}, s)
rXs := xmult(r, s)
// 求解t, u
// t = (q-p)Xs/(rXs)
t := float64(qps) / float64(rXs)
if !isInRange01(t) {
return []float64{}
}
// u = (q-p)Xr/(rXs)
u := float64(qpr) / float64(rXs)
if !isInRange01(u) {
return []float64{}
}
p0 := getPoint(p, r, t)
return p0
}
func intersectionArr(arr []int) {
a1:=intersection(arr[0:2], arr[2:4], arr[4:6], arr[6:8])
//a2:=intersection2(arr[0:2], arr[2:4], arr[4:6], arr[6:8])
fmt.Println(a1)
}
/*
func main() {
intersectionArr([]int{0, 0, 1, 0, 1, 1, 0, -1})
intersectionArr([]int{0, 0, 3, 3, 1, 1, 2, 2})
intersectionArr([]int{0, 0, 1, 1, 1, 0, 2, 1})
intersectionArr([]int{0, 0, 10, 0, 10, 0, 11, 0})
intersectionArr([]int{10, 0, 0, 0, -10, 0, -11, 0})
intersectionArr([]int{0, 10, 0, 20, 1, -1, -1, 1})
intersectionArr([]int{0, 10, 0, 0, 1, -1, -1, 1})
intersectionArr([]int{10, 0, -10, 0, 11, -1, -1, 1})
intersectionArr([]int{10, -10, -10, 10, 10, -10, -10, 10})
intersectionArr([]int{10, -10, -10, 10, -10, -10, 10, 10})
intersectionArr([]int{1000, -1123, -1123, 1333, -1000, -1000, 1000, 1000})
intersectionArr([]int{1000, 0, 2000, 0, 1000, 1, 2000, 1})
intersectionArr([]int{1000, 123, 2000, -123, 1000, 1, 2000, -123})
intersectionArr([]int{1000, 123, 2000, -123, 1000, 1, 2000, -123})
intersectionArr([]int{1000, 0, 2000, 0, 2000, 0, 2000, 1})
intersectionArr([]int{-1000, -1000, 1000, 1000, 2000, 2000, 3000, 3000})
intersectionArr([]int{-1000, -1000, 1000, 1000, -2000, -2000, 3000, 3000})
intersectionArr([]int{-1000, -1000, 1000, 1000, -2000, -2000, 500, 500})
intersectionArr([]int{-1000, -1000, 1000, 1000, 500, 500, -2000, -2000})
intersectionArr([]int{500, 500, -2000, -2000,-1000, -1000, 1000, 1000})
}
*/
应用练习
题目:https://leetcode-cn.com/problems/bisect-squares-lcci/
题目大意
给定两个正方形及一个二维平面。请找出将这两个正方形分割成两半的一条直线。假设正方形顶边和底边与 x 轴平行。
每个正方形的数据square包含3个数值,正方形的左下顶点坐标[X,Y] = [square[0],square[1]],以及正方形的边长square[2]。所求直线穿过两个正方形会形成4个交点,请返回4个交点形成线段的两端点坐标(两个端点即为4个交点中距离最远的2个点,这2个点所连成的线段一定会穿过另外2个交点)。2个端点坐标[X1,Y1]和[X2,Y2]的返回格式为{X1,Y1,X2,Y2},要求若X1 != X2,需保证X1 < X2,否则需保证Y1 <= Y2。
若同时有多条直线满足要求,则选择斜率最大的一条计算并返回(与Y轴平行的直线视为斜率无穷大)。
示例:
输入:
square1 = {-1, -1, 2}
square2 = {0, -1, 2}
输出: {-1,0,2,0}
解释: 直线 y = 0 能将两个正方形同时分为等面积的两部分,返回的两线段端点为[-1,0]和[2,0]
提示:
square.length == 3
square[2] > 0
题目解析
经过正方形对角线交点(中点)的线就可以平分正方形。
所以,先由两个正方形的中点确定一条直线。然后用这条直线求出与2个正方形所有边的交点,从这几个交点中找出最左,最右的点。
特殊情况
当两个中点x轴相同时,此时,平分直线要垂直于x轴即可。
与普通线段求交相比,这里平分线是一条直线(无线长),不用判断交点是否平分线上。
AC代码
package main
import (
"fmt"
"math"
)
var esp float64 = 1e-6
// 比较浮点型:0 相等,1 >, -1 <
func cmpDouble(a, b float64) int {
if math.Abs(a-b) < esp {
return 0
}
if a < b {
return -1
}
return 1
}
func xmult(p1, p2 []float64) float64 {
return p1[0]*p2[1] - p1[1]*p2[0]
}
// 点积
func dotProduct(a, b []float64) float64 {
return float64(a[0]*b[0] + a[1]*b[1])
}
func getPoint(p, r []float64, t float64) []float64 {
p0 := float64(p[0]) + t*float64(r[0])
p1 := float64(p[1]) + t*float64(r[1])
return []float64{p0, p1}
}
// 共线求解交点
// t0 = (q-p)*r/(r*r)
// t1 = (q+s-p)*r/(r*r) = t0 + s · r / (r · r)
func getOnlinePoint(q []float64, s []float64, p []float64, r []float64) []float64 {
t0 := dotProduct([]float64{q[0] - p[0], q[1] - p[1]}, r) / dotProduct(r, r)
t1 := t0 + dotProduct(s, r)/dotProduct(r, r)
if cmpDouble(t0, t1) > 0 {
t0, t1 = t1, t0
}
// 没有交集
if t1 < 0 || t0 > 1 {
return []float64{}
}
// 与 [0, 1]区间求交集
t0 = math.Max(0, t0)
t1 = math.Min(1, t1)
// 求解起终点
p0 := getPoint(p, r, t0)
p1 := getPoint(p, r, t1)
// 查看x轴小的先返回
if cmpDouble(p1[0], p0[0]) < 0 {
p0 = p1
} else if cmpDouble(p1[0], p0[0]) == 0 && cmpDouble(p1[1], p0[0]) < 0 { // x 轴相同比较y轴
p0 = p1
}
return p0
}
func isInRange01(t float64) bool {
if t < 0 || t > 1 {
return false
}
return true
}
/*
点p 到 p+r 表示线段1
点q 到 q+s 表示线段2
线段1 上1点用 p' = p+t*r (0<=t<=1)
线段2 上1点用 q' = q+u*s (0<=u<=1)
让两式相等求交点 p+t*r = q+u*s
两边都叉乘s
(p+t*r)Xs = (q+u*s)Xs
pXs + t*rXs = qXs
t = (q-p)Xs/(rXs)
同理,
u = (p-q)Xr/(sXr) -> u = (q-p)Xr/(rXs)
以下分4种情况:
1. 共线,sXr==0 && (q-p)Xr==0, 计算 (q-p)在r上的投影在r长度上的占比t0,
计算(q+s-p)在r上的投影在r长度上的占比t1,查看[t0, t1]是否与范围[0,1]有交集。
如果t0>t1, 则比较[t1, t0]是否与范围[0,1]有交集。
t0 = (q-p)*r/(r*r)
t1 = (q+s-p)*r/(r*r) = t0 + s · r / (r · r)
2. 平行sXr==0 && (q-p)Xr!=0
3. 0<=u<=1 && 0<=t<=1 有交点
4. 其他u, t不在0到范围内,没有交点。
*/
func intersection(q []float64, end1 []float64, p []float64, end2 []float64) []float64 {
s := []float64{end1[0] - q[0], end1[1] - q[1]}
r := []float64{end2[0] - p[0], end2[1] - p[1]}
// 计算 (q-p)Xr
qpr := xmult([]float64{q[0] - p[0], q[1] - p[1]}, r)
// 平分线不可能与正方形边生命,如果平行一定是没有交点
if xmult(s, r) == 0 {
return []float64{}
}
qps := xmult([]float64{q[0] - p[0], q[1] - p[1]}, s)
rXs := xmult(r, s)
// 求解t, u
// t = (q-p)Xs/(rXs)
t := float64(qps) / float64(rXs)
// 不需要检查t的范围
/*
if !isInRange01(t) {
return []float64{}
}*/
// u = (q-p)Xr/(rXs)
u := float64(qpr) / float64(rXs)
if !isInRange01(u) {
return []float64{}
}
p0 := getPoint(p, r, t)
return p0
}
// 获取正方形顶点
func getVertex(square1 []int) [][]float64 {
dir := [][]int{
{0,1},
{1,0},
{0, -1},
}
points := [][]float64{{float64(square1[0]),float64( square1[1])}}
for i := 0; i < 3; i++ {
points = append(points, []float64{points[i][0] + float64(dir[i][0]*square1[2]), points[i][1] + float64(dir[i][1]*square1[2])})
}
return points
}
func cutSquares(square1 []int, square2 []int) []float64 {
// 通过2个正方形中点作直线,可以平分
p1 := []float64{float64(square1[0]) + float64(square1[2])/2, float64(square1[1]) + float64(square1[2])/2}
p2 := []float64{float64(square2[0]) + float64(square2[2])/2, float64(square2[1]) + float64(square2[2])/2}
// 中心相同,斜率为下无穷大
if cmpDouble(p1[0], p2[0]) == 0 && cmpDouble(p1[1], p2[1]) == 0 {
p2 = []float64{p1[0], p1[1] + 1}
}
// 与8条边求出8个交点,有可能没有。
ps := [][]float64{}
sqps := getVertex(square1)
for i := 0; i < 4; i++ {
cp := intersection(sqps[i], sqps[(i+1)%4], p1, p2)
if len(cp) == 0 {
continue
}
ps = append(ps, cp)
}
sqps = getVertex(square2)
for i := 0; i < 4; i++ {
cp := intersection(sqps[i], sqps[(i+1)%4], p1, p2)
if len(cp) == 0 {
continue
}
ps = append(ps, cp)
}
left := ps[0]
right := ps[0]
for _, p := range ps {
if p[0] < left[0] || (cmpDouble(p[0], left[0]) == 0 && p[1] < left[1]) {
left = p
}
if p[0] > right[0] || (cmpDouble(p[0], right[0]) == 0 && p[1] > right[1]) {
right = p
}
}
return []float64{left[0], left[1], right[0], right[1]}
}
本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。
![]()