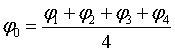MATLAB求解接地金属槽内电位分布

要求

运用MATLAB求解接地金属槽内点位分布， 精度、行数M、列数N自己定义。

有限差分法

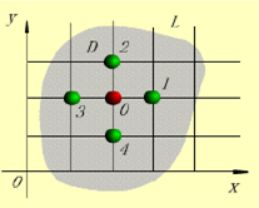
有限差分法是基于差分原理的一种数值计算法。其基本思想想是将场域离散成很多许多小的网格，应用差分原理，将求解连续函数的柏松方程问题转换为求解网格节点上的差分方程组问题。

有限差分法网格划分→

拉普拉斯方程的五点差分格式：

可通过迭代法求解以上差分方程。

MATLAB编写

① 由高斯—赛德尔迭代法，将网格分成M*N列→

x=100;y=60;
v1=zeros(y,x);

先假设金属槽长为100，宽为60。 通过zeros()函数生成一个 x*y 的零矩阵


② 将金属槽顶端的值设置为5（V）→

for j=2:x-1
v1(y,j)=5;
end

金属槽顶端对应的矩阵坐标为 v1(60,2) ~ v1(60,99) , 通过for循环对顶端点进行一一赋值


③ 开始迭代→

v2=v1;m=1;t=0;k=0;
while(m>0.0000001)
k=k+1;     
m=0;
for i=2:y-1
for j=2:x-1;
v2(i,j)=(v1(i,j+1)+v1(i+1,j)+v1(i-1,j)+v1(i,j-1))/4;
t=(v2(i,j)-v1(i,j));  
if(t>m)m=t;end
end
end
v1=v2;
end

首先迭代开始之前将另一个数组 v2 赋值，用数组 v1 给其赋值，表示迭代之前的值，好用于后面精度的比较，定义变量 m 表示精度， 变量 t 表示点位实际差值，变量 k 表示迭代次数。

开始进行迭代时，根据公式将迭代方程编写输入即
v2( i , j )=(v1 ( i , j + 1 ) + v1 ( i+1 , j ) + v1 ( i - 1 , j ) + v1 ( i , j-1 )) / 4 。

每次迭代结束后将数组 v1 和数组 v2 对应的值进行比较，即是精度的计算。

如果误差大于所规定的误差0.0000001，将 v1 的值赋给 v2 ，然后继续进行迭代。

直到当迭代前后数值误差小于所规定的误差时停止迭代。


④ 绘制图像→

subplot(2,1,1),mesh(v1)  
axis([0,100,0,60,0,5])   %x,y,z 坐标范围
title('①金属槽电位三维网络图')
subplot(2,1,2),contour(v2,40)  %矩阵的等高线图
title('②金属槽等电位图')

axis([0,62,0,101,0,5]) 设置x,y,z 坐标范围
通过mesh() 函数绘制金属槽电位三维图；
通过contour() 函数获取 金属槽等电位图 ；“40”表示取40条等值线。
并加上图片标题。

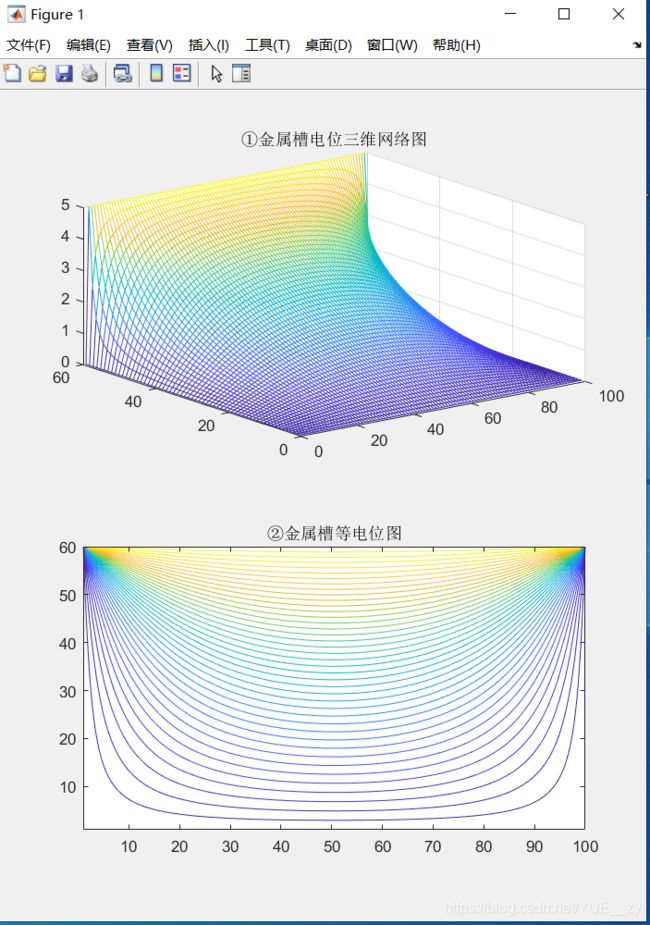
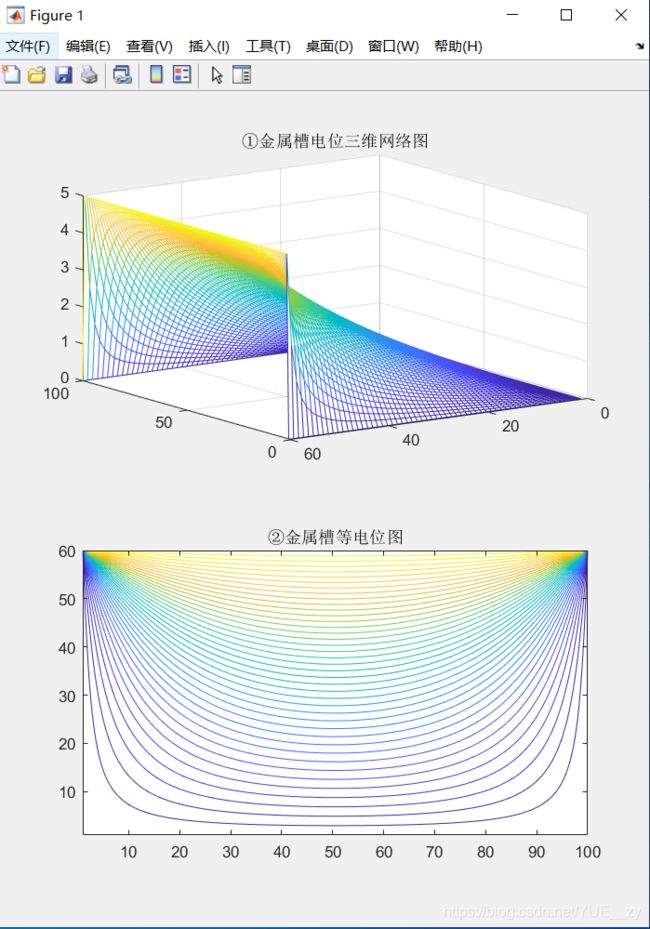
运行结果

在MATLAB中将代码写好后，运行得到图像→

将三维网络图旋转，电位观察更直观

将光标放置在图像中，即可获取电位值。 （Z值 和 Level值 ）
程序运行完后的 k 值即为迭代次数。

\

全部代码

x=100;y=60;
v1=zeros(y,x); %生成一个lx*ly的零矩阵
for j=2:x-1 %将金属块顶端设置为5V
v1(y,j)=5;
end
v2=v1;m=1;t=0;k=0;
while(m>0.0000001)
k=k+1; %迭代次数
m=0;
for i=2:y-1
for j=2:x-1;
v2(i,j)=(v1(i,j+1)+v1(i+1,j)+v1(i-1,j)+v1(i,j-1))/4;
t=(v2(i,j)-v1(i,j)); % v2 与 v1 偏差
if(t>m)m=t;end %精度比较
end
end
v1=v2;
end
k
subplot(2,1,1),mesh(v1) %网络图
axis([0,62,0,101,0,5]) %x,y,z 坐标范围
title(‘①金属槽电位三维网络图’)
subplot(2,1,2),contour(v2,40) %矩阵的等高线图
title(‘②金属槽等电位图’)

%designer：YUE
注：复制代码时可能会有中文报错，需将中文符号改成英文符号