nsgaⅢ算法
1.nsgaⅢ算法总框架
nasga3算法框架分为三个部分:
(1)初始化种群,随机产生种群规模为N的父代种群pt
(2)更新种群,pt种群通过交叉变异产生新的规模为N的子代种群qt(SBX,多项式变异)
(3)选择操纵,通过选择机制从rt=pt∪qt(种群规模为2N)选出优秀的规模为N的种群
1.1更新操作
1.SBX
2.多项式变异
1.2 选择机制
1.第一步采用非支配排序将种群RT分成不同的非支配曾(F1,F2,F3…)
2.当\F1∪F2∪…∪Fl-1\<N,但\F1∪F2∪…∪Fl\>N时,定义Fl为临界层,采用临界层选择方法选择个体进入下一代,直到子代种群大小等于N。
2.1 临界层选择方法:
nsga2算法通过拥挤度选择具有良好分布的个体,而nsga3通过参考点的方式选择合适的个体。
参考点设置方法:Das和Dennis在1998年提出的边界交叉构造权重的方法。
在标准化参考平面上,如果每一维目标被均匀地分割成p份,那么均匀地产生C(m+p-1,p)个参考点,具体图参考以下博文。
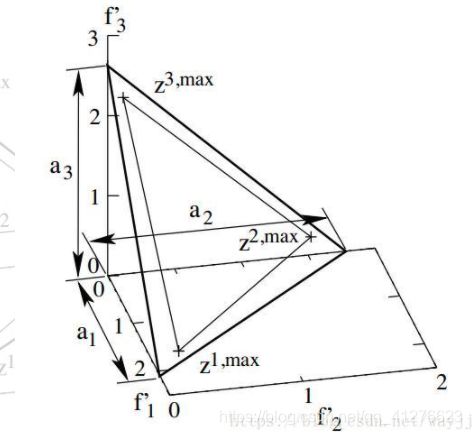
2)超平面
由maxf1,maxf2,maxf3三点连线所构成的平面
https://blog.csdn.net/xuxinrk/article/details/82965280?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522160090773019721941930663%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=160090773019721941930663&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allfirst_rank_ecpm_v3~pc_rank_v2-2-82965280.first_rank_ecpm_v3_pc_rank_v2&utm_term=nsga3&spm=1018.2118.3001.4187
2.1 极值点
三维目标下,对于在一个方向上目标值很大,另两个方向上目标值很小的点,计算其极值点:
例如:A(1,0.2,0.3); B(1,0.6,0.3); C(1,0.1,0.2),固定第一个坐标轴(即w=(1,0,0)),计算ASF(x,w),有
ASFA(x,w)=MAX(1,0.2,0.3)/ (1,10-6, 10-6)=MAX{1,0.210-6, 0.310-6}=0.3*10-6
ASFB(x,w)= MAX(1,0.6,0.3)/ (1,10-6, 10-6)= MAX{1,0.610-6, 0.310-6}=0.6*10-6
ASFC(x,w)= MAX(1,0.1,0.2)/ (1,10-6, 10-6)= MAX{1,0.110-6, 0.210-6}=0.2*10-6
因为每一维坐标的极大值点Zi,max取ASFi(x,w)的最小值,即极值点为使得ASFi(x,w)最小的点,而ASFC(x,w) =0.2*10-6最小,对应的极值点为(1,0.1,0.2)。同理可以计算出第二维和第三维对应的极值点。
2.2 截距
三维目标下,由极值点计算方法可计算出三个极值点。例如Z1(-1,1,2),Z2(2,0,-3),Z3(5,1,-2).
对于方程ax+by+cz=1,将Z1,Z2,Z3分别代入方程中得a=-0.4,b=1.8,c=-0.6。从而可得-0.4x+1.8y±0.6z=1
令y=0,z=0,则x=-5/2
令x=0,z=0,则y=5/9
令x=0,y=0,则z=-5/3
从而得到截距a1=-5/2;a2=5/9;a3-5/3.
2.3标准化计算公式
其中ai为第i维的截距,求和fn,i(x)=1(i=1…M)。
3,关联操作
(1)将参考点与原点连线作为该参考点在目标空间的中的参考线;
(2)计算St中个体到各参考线的距离,个体距离哪条参考线近,就与哪条参考线对应的参考点相关联。